Baccalauréat S Centres étrangers 12 juin 2014 - Correction Exercice 3
Exercice 3 7 points
- $x = 0$ pour le blanc ;
- $x = 1$ pour le noir;
- $x = 0,01 \:;\: x = 0,02$ et ainsi de suite jusqu'à $x = 0,99$ par pas de $0,01$ pour toutes les nuances intermédiaires (du clair au foncé).
L'image A, ci-après, est composée de quatre pixels et donne un échantillon de ces nuances avec leurs codes. Un logiciel de retouche d'image utilise des fonctions numériques dites « fonctions de retouche » . Une fonction $f$ définie sur l'intervalle [0 ; 1] est dite « fonction de retouche » si elle possède les quatre propriétés suivantes :
- $f(0) = 0$ ;
- $f(1) = 1$ ;
- $f$ est continue sur l'intervalle [0 ; 1] ;
- $f$ est croissante sur l'intervalle [0 ; 1].
Une nuance codée $x$ est dite assombrie par la fonction $f$ si $f(x) > x$, et éclaircie, si $f(x) < x$. Ainsi, si $f(x) = x^2$, un pixel de nuance codée $0,2$ prendra la nuance codée $0,2^2 = 0,04$. L'image A sera transformée en l'image B ci-dessous. Si $f(x) = \sqrt{x}$, la nuance codée $0,2$ prendra la nuance codée $\sqrt{0,2} \approx 0,45$. L'image A sera transformée en l'image C ci-dessous.

Partie A
- On considère la fonction $f_{1}$ définie sur l'intervalle [0 ; 1] par : \[f_{1}(x) = 4x^3 - 6x^2 + 3x.\]
- Démontrer que la fonction $f_{1}$ est une fonction de retouche. $f_1(0) = 4\times 0^3 – 6\times 0^2 + 3\times 0 = 0$
- $f_1(1) = 4 – 6 + 3 = 1$
- $f_1$ est un polynôme. Elle est donc continue et dérivable sur $[0;1]$.
- $f_1′(x) = 12x^2-12x+3 = 3(4^2-4x+1)$ $=3(2x-1)^2 \ge 0$
- Donc $f_1$ est croissante sur $[0;1]$.
- $f_1$ est bien une fonction de retouche.
- Résoudre graphiquement l'inéquation $f_{1}(x) \leqslant x$, à l'aide du graphique donné en annexe, à rendre avec la copie, en faisant apparaître les pointillés utiles. Interpréter ce résultat en termes d'éclaircissement ou d'assombrissement.

- L'ensemble des solutions de $f_1(x) \le x$ est donc, graphiquement, $[0,5;1]\cup{0}$.
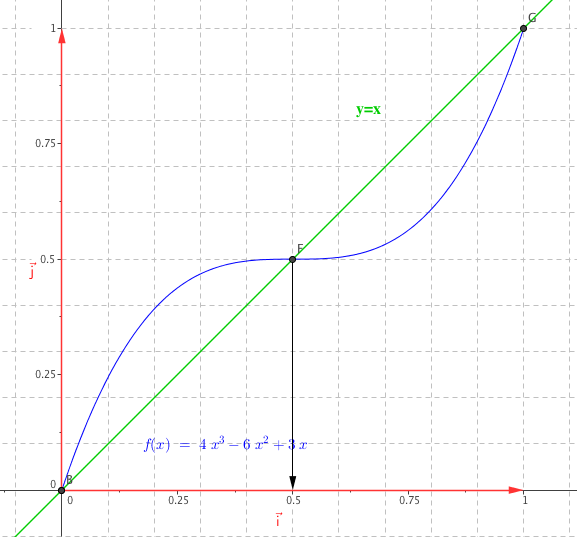
- Cela signifie donc que la fonction $f_1$ assombrit les nuances inférieures à $0,5$ et éclaircit celles supérieures à $0,5$.
- On considère la fonction $f_{2}$ définie sur l'intervalle [0 ; 1] par : \[f_{2}(x) = \ln [1 + (\text{e} - 1)x].\] On admet que $f_{2}$ est une fonction de retouche. On définit sur l'intervalle [0 ; 1] la fonction $g$ par : $g(x) = f_{2}(x) - x$.
- Établir que, pour tout $x$ de l'intervalle [0 ; 1] : $g'(x) = \dfrac{(\text{e} - 2) - (\text{e} - 1)x}{1 + (\text{e} - 1)x}$ ; $$\begin{array}\\ g’(x) &= f_2′(x) – 1 \\ &=\dfrac{\text{e} – 1}{1 + (\text{e} – 1)x} – 1 \\ &=\dfrac{\text{e} – 1 – 1 – (\text{e} – 1)x}{1 + (\text{e} – 1)x} \\ &=\dfrac{(\text{e} – 2) - (\text{e} – 1)x}{1 + (\text{e} – 1)x} \end{array}$$
- Déterminer les variations de la fonction $g$ sur l'intervalle [0 ; 1]. Démontrer que la fonction $g$ admet un maximum en $\dfrac{\text{e} - 2}{\text{e} - 1}$, maximum dont une valeur arrondie au centième est $0,12$. Pour tout $x \in [0;1] 0 \le 1 + (\text{e}-1)x$
- Donc le signe de $g’(x)$ ne dépend que de celui du numérateur.
- $$\begin{array} (\text{e} – 2) - (\text{e} – 1)x \ge 0 & \Leftrightarrow (\text{e} – 2) \ge (\text{e} – 1)x \\ & \Leftrightarrow x \le \dfrac{(\text{e} – 2)}{(\text{e} – 1)} = \alpha \end{array}$$
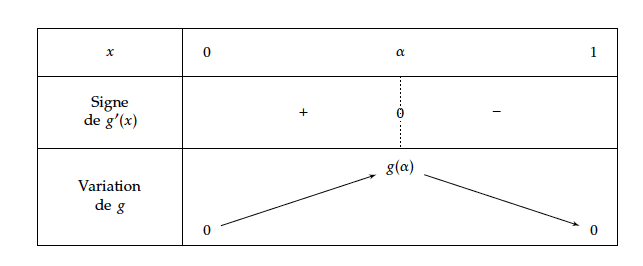
- et $g(\alpha) \approx 0,12$
- La fonction $g$ admet donc un maximum en $\alpha$
- Établir que l'équation $g(x) = 0,05$ admet sur l'intervalle [0 ; 1] deux solutions $\alpha$ et $\beta$, avec $\alpha < \beta$. On admettra que : $0,08 < \alpha < 0,09$ et que : $0,85 < \beta < 0,86$.
La fonction $g$ est continue et strictement croissante sur $[0;\alpha]$.
- $g(0) = 0$ et $g(\alpha) \approx 0,12$
- Par conséquent $0,05 \in [0;0,12]$.
- D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $g(x) = 0,05$ possède une unique solution sur $[0;\alpha]$.$~$
- La fonction $g$ est continue et strictement décroissante sur $[\alpha;1]$.
- $g(1) = 0$ et $g(\alpha) \approx 0,12$
- Par conséquent $0,05 \in [0;0,12]$.
- D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $g(x) = 0,05$ possède une unique solution sur $[0;\alpha]$.$~$
- Par conséquent l’équation $g(x) = 0$ possède bien deux solutions
- $g(0,08) \approx 0,049$ et $g(0,09) \approx 0,054$
- Donc la première solution est bien comprise entre $0,08$ et $0,09$.
- $~$
- $g(0,85) \approx 0,0504$ et $g(0,86) \approx 0,0473$
- donc la deuxième solution est bien comprise entre $0,85$ et $0,86$.
On remarque qu'une modification de nuance n'est perceptible visuellement que si la valeur absolue de l'écart entre le code de la nuance initiale et le code de la nuance modifiée est supérieure ou égale à $0,05$.
- Dans l'algorithme décrit ci-dessous, $f$ désigne une fonction de retouche. Quel est le rôle de cet algorithme ? $$\begin{array}{ | l|l|} \hline \text{Variables :}& x \text{ (nuance initiale)}\\ &y \text{ (nuance retouchée) }\\ &E \text{ (écart)}\\ &c \text{ (compteur)}\\ & k\\ \text{Initialisation :}& c \text{ prend la valeur 0 }\\ \text{Traitement :}& \text{ Pour } k \text{ allant de 0 à 100, faire}\\ & \begin{array}{l|l l}\\ &x \text{ prend la valeur } \frac{k}{100}&\\ &y \text{ prend la valeur } f(x)& \\ &E \text{ prend la valeur } |y - x|&\\ &&\begin{array}{l| l } &\text{ Si } E > \text{0,05, faire } \\ & \quad c \text{ prend la valeur } c + 1\\ & \text{ Fin si } \end{array} \end{array} \\ &\text{ Fin pour }\\ \text{Sortie :}& \text{ Afficher } c \\ \hline \end{array}$$
- Quelle valeur affichera cet algorithme si on l'applique à la fonction $f_{2}$ définie dans la deuxième question de la Partie A ? On cherche donc les valeurs de $x$ telles que $f_2(x) – x \ge 0,05$ c’est-à-dire $g(x) \ge 0,05$.
- Ce sont donc toutes les nuances comprises entre les $2$ solutions $\alpha$ et $\beta$ de la partie précédente.
- On va donc prendre toutes les nuances comprises entre $0,09$ et $0,85$. Il y en a par conséquent $85 – 9 + 1 = 77$.
- $~$
- L’algorithme affichera donc $77$.
Dans cette partie, on s'intéresse à des fonctions de retouche $f$ dont l'effet est d'éclaircir l'image dans sa globalité, c'est-a-dire telles que, pour tout réel $x$ de l'intervalle [0 ; 1], $f(x) \leqslant x$.
On décide de mesurer l'éclaircissement global de l'image en calculant l'aire $\mathcal{A}_{f}$ de la portion de plan comprise entre l'axe des abscisses, la courbe représentative de la fonction $f$, et les droites d'équations respectives $x = 0$ et $x = 1$. Entre deux fonctions, celle qui aura pour effet d'éclaircir le plus l'image celle correspondant à la plus petite aire.
On désire comparer l'effet des deux fonctions suivantes, dont on admet qu'elles sont des fonctions de retouche :
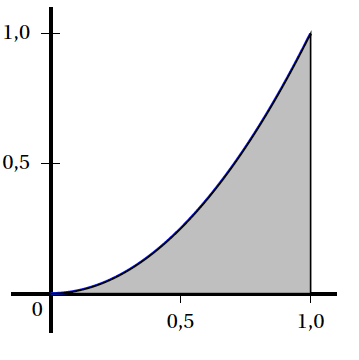
\[f_{1}(x) = x \text{e}^{\left(x^2 - 1 \right)}\qquad f_{2}(x) = 4x - 15 + \dfrac{60}{x+4}.\]
- Calculer $\mathcal{A}_{f_{1}}$. $\mathcal{A_{f_1}} = \displaystyle \int_0^1 f_1(x)\text{d}x $.
- Une primitive de $f_1$ est $F_1$ définie par $F_1(x) = 0,5\text{e}^{x^2-1}$
- Donc $\mathcal{A_{f_1}} = F_1(1) – F_1(0) = 0,5 – 0,5\text{e}^{-1}$ u.a. $\approx 0,316$
- Calculer $\mathcal{A}_{f_{2}}$ $\mathcal{A_{f_2}} = \displaystyle \int_0^1 f_2(x)\text{d}x $.
- Une primitive de $f_2$ est $F_2$ définie par $F_2(x) =2x^2-15x+60\ln (x+4)$
- Donc $\mathcal{A_{f_2}} = F_2(1) – F_2(0) = -13 +60 \ln 5 – 60 \ln(4) $ u.a. $\approx 0,389$
- De ces deux fonctions, laquelle a pour effet d'éclaircir le plus l'image ? La fonction $f_1$ a donc l’aire la plus petite. C’est elle qui aura pour effet d’éclaircir le plus l’image.
- Vues: 40520
