Baccalauréat S Centres étrangers 12 juin 2014 - Correction Exercice 2
Page 4 sur 11
Exercice 2 4 points
On définit, pour tout entier naturel $n$, les nombres complexes $z$ par : \[\left\{\begin{array}{l c l} z_{0}&=& 16\\ z_{n+1}&=&\dfrac{1 + \text{i}}{2}z_{n},\: \text{pour tout entier naturel} \: n. \end{array}\right.\]
On note $r_{n}$ le module du nombre complexe $z_{n}\: : r_{n} =\left|z_{n}\right|$. Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.
On note $r_{n}$ le module du nombre complexe $z_{n}\: : r_{n} =\left|z_{n}\right|$. Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.
- Calculer $z_{1}, z_{2}$ et $z_{3}$. $z_2 = \dfrac{1+\text{i}}{2}\times 8(1 + \text{i}) $ $=8i$
- $z_3 = \dfrac{1+\text{i}}{2}\times 8\text{i} = -4 + 4\text{i}$
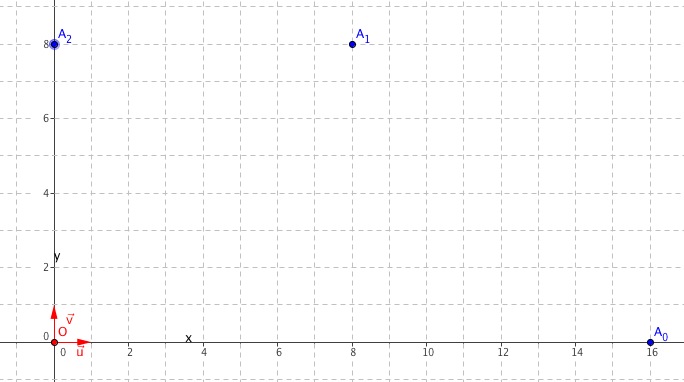
- Placer les points $A_{1}$ et $A_{2}$ sur le graphique de l' annexe, à rendre avec la copie .
- Écrire le nombre complexe $\dfrac{1 + \text{i}}{2}$ sous forme trigonométrique. $\left| \dfrac{1+\text{i}}{2} \right| = \dfrac{\sqrt{2}}{2}$
- Donc $\dfrac{1+\text{i}}{2} = \dfrac{\sqrt{2}}{2} \left(\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2} \text{i} \right)$ $=\dfrac{\sqrt{2}}{2} \left( \cos \dfrac{\pi}{4} + \text{i} \sin \dfrac{\pi}{4} \right) $ $\quad \left(= \dfrac{\sqrt{2}}{2} \text{e}^{\text{i}\pi/4} \right)$
- Démontrer que le triangle O$A_{0}A_{1}$ est isocèle rectangle en $A_{1}$. $OA_1 = |z_1| = 8\sqrt{2}$
- $A_1A_0 = |z_0 – z_1| $ $=|8 – 8\text{i} | $ $=8\sqrt{2}$
- $OA_0 = |z_0| = 16$
- Le triangle $OA_0A_1$ est bien isocèle en $A_1$.
- De plus $16^2 = 2 \times \left( 8\sqrt{2} \right)^2$ donc $OA_0^2 = OA_1^2+A_1A_0^2$
- D’après la réciproque du théorème de Pythagore, le triangle est également rectangle en $A_1$.
- Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$. La suite $\left(r_{n}\right)$ est-elle convergente ? Interpréter géométriquement le résultat précédent. $$\begin{array}{ll} r_{n+1} &=|z_{n+1}| \\ & = \left| \dfrac{1+\text{i}}{2} \right| \times |z_n| \\ &=\dfrac{\sqrt{2}}{2} r_n\\ \end{array}$$ La suite $(r_n)$ est donc bien géométrique de raison $\dfrac{\sqrt{2}}{2}$.
- $0 < \dfrac{\sqrt{2}}{2}< 1$ donc $\lim\limits_{n \rightarrow +\infty} \left(\dfrac{\sqrt{2}}{2} \right)^n = 0$
- Par conséquent $\lim\limits_{n \rightarrow +\infty} r_n = 0$
- $~$
- Cela signifie donc que la distance $OA_n$ tend vers $0$ et que donc le point $A_n$ « se rapproche » de O.
On note $L_{n}$ la longueur de la ligne brisée qui relie le point $A_{0}$ au point $A_{n}$ en passant successivement par les points $A_{1}, A_{2}, A_{3}$, etc. Ainsi $L_{n} = \displaystyle\sum_{i=0}^{n-1} A_{i}A_{i+1} = A_{0}A_{1} + A_{1}A_{2} + \ldots + A_{n-1}A_{n}.$
- Démontrer que pour tout entier naturel $n \::\: A_{n}A_{n+1} = r_{n+1}$. $$ \begin{array} \\A_{n}A_{n+1} &= |z_{n+1}-z_n| \\ & = \left|\dfrac{1+\text{i}}{2}z_n -z_n \right| \\ & = \left|\dfrac{-1+\text{i}}{2}z_n \right| \\ &= \dfrac{\sqrt{2}}{2} |z_n| \\ &= r_{n+1} \end{array}$$
- Donner une expression de $L_{n}$ en fonction de $n$. On a donc :
- $$\begin{array}\\ L_{n}&= \sum_{i=0}^{i=n-1} r_{i+1} \\ & = r_1+r_2+\ldots+r_n \\ & = 8\sqrt{2} \dfrac{1-\left(\dfrac{\sqrt{2}}{2} \right) ^n}{1 - \dfrac{\sqrt{2}}{2}}\\ \end{array}$$
- On utilise la formule donnant la somme d’une suite géométrique :
- $$ 1^\text{er}\text{ terme} \times \dfrac{1 – \text{raison}^\text{nombre de termes}}{1 – \text{raison}}$$
- Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$. On a vu que $\lim\limits_{n \rightarrow +\infty} \left(\dfrac{\sqrt{2}}{2} \right)^n = 0$.
- Par conséquent $\lim\limits_{n \rightarrow +\infty} L_n = \dfrac{8\sqrt{2}}{1 - \dfrac{\sqrt{2}}{2}}$ $=16 + 16\sqrt{2}$
- Vues: 40842
