Baccalauréat S Centres étrangers 12 juin 2014 - Correction Exercice 1
Exercice 1 4 points
Aucune justification n'est demandée. Une réponse exacte rapporte un point ; une réponse fausse ou une absence de réponse ne rapporte ni n'enlève de point.
Une femme sur cinq achète un article au rayon bricolage, alors que sept hommes sur dix le font. Une personne, choisie au hasard, a fait un achat au rayon bricolage.
La probabilité que cette personne soit une femme a pour valeur arrondie au millième :
- 0,750
- 0,150
- 0,462
- 0,700
On appelle $F$ l’événement la personne est une femme et $B$ l’événement la personne achète un article au rayon bricolage. On obtient alors l’arbre suivant : 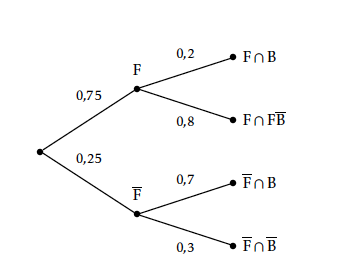
Par conséquent, d’après la propriété des probabilités totales, on a : $$\begin{array} p(B) &=p(B \cap F) + p\left(B \cap \bar{F} \right) \\\\ &= 0,75 \times 0,2 + 0,25 \times 0,7 \\\\ & = 0,325 \end{array}$$ On cherche à connaître : $$\begin{array} p_B(F) &= \dfrac{p(B \cap F)}{p(B)} \\\\ &= \dfrac{0,75 \times 0,2}{0,325} \\\\ &\approx 0,462 \end{array}$$
Réponse c
Une étude statistique a permis d'établir que, chaque fois qu'un client s'intéresse à ce modèle, la probabilité qu'il l'achète est égale à $0,3$.
On considère un échantillon aléatoire de dix clients qui se sont intéressés à ce modèle.
La probabilité qu'exactement trois d'entre eux aient acheté un ordinateur de ce modèle a pour valeur arrondie au millième :
- 0,900
- 0,092
- 0,00
- 0,267
On appelle $X$ la variable aléatoire qui compte le nombre de clients ayant acheté un ordinateur de ce modèle.
Il y a 10 « tirages », tous identiques, aléatoires et indépendants.
Chaque tirage ne possède que 2 issues : $A$ « le client a acheté un ordinateur » de probabilité $p(A)=0,3$ et $\overline{A}$ ...
La variable aléatoire $X$ suit donc la loi binomiale $\mathcal{B}(10;0,3)$. Donc $P(X=3)=\binom{10}{3} \times 0,3 ^3\times 0,7^7 \approx 0,267$
Réponse d
La durée de vie moyenne d'un téléviseur est de huit ans, ce qui se traduit par : $\lambda = \dfrac{1}{8}$.
La probabilité qu'un téléviseur pris au hasard fonctionne encore au bout de six ans a pour valeur arrondie au millième :
- 0,750
- 0,250
- 0,472
- 0,528
On appelle $T $ la variable aléatoire suivant la loi exponentielle de paramètres $\lambda=18$.
On calcule donc $$P(T\geq 6)=e^{−6\lambda} \approx 0,472 $$
Réponse c.
La probabilité que la masse d'une baguette soit comprise entre 184 g et 216 g est égale à $0,954$.
La probabilité qu'une baguette prise au hasard ait une masse inférieure à 192 g a pour valeur arrondie au centième :
- 0,16
- 0,32
- 0,84
- 0,48
On appelle $Y$ la variable aléatoire suivant la loi normale $\mathcal{N}(200;\sigma^2).$
D’après le cours on sait que $P(200−2\sigma \leq Y\leq 200+2\sigma )=0,954.$
Or ici on sait que $P(184\leq Y\leq 216)=0,954.$
Par conséquent $2\sigma =16$ soit $\sigma =8$
On en déduit donc que $P(Y\leq 192)=0,5–P(192\leq Y\leq 200) \approx 0,16.$
Réponse a
- Vues: 40934
