Baccalauréat S Métropole 19 juin 2014

Page 1 sur 10

 Le sujet en pdf

Le corrigé en pdf

Exercice 1 5 points

Commun à tous les candidats

Partie A

Dans le plan muni d'un repère orthonormé, on désigne par $\mathcal{C}_1$ la courbe représentative de la fonction $f_1$ définie sur $\mathbb{R}$ par : $$f_1(x)=x+e^{-x}$$

1. Justifier que $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
2. Déterminer le tableau de variation de la fonction $f_1$. Onprécisera les limites de $f_1$ en $+\infty$ et en $-\infty$ .

Partie B

L 'objet de cette partie est d'étudier la suite $\left (I_n\right )$ définie sur $\mathbb{R}$ par : $I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$

1. Dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, pour tout entier naturel $n$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ définie sur $\mathbb{R}$ par : $$f_n(x)=x+e^{-nx}$$
   
   Sur le graphique ci-dessous on a tracé la courbe $\mathcal{C}_n$ pour plusieurs valeurs de l'entier $n$ et la droite $\mathcal{D}$ d'équation $x=1$.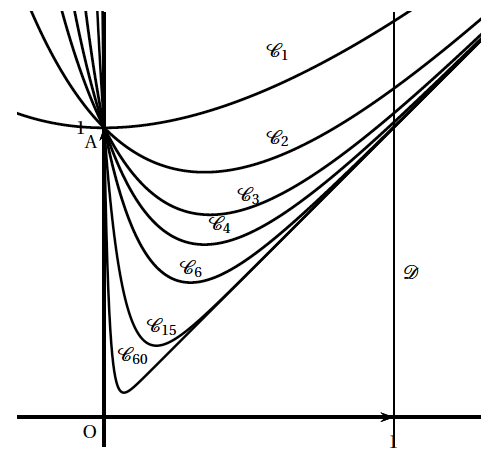
   1. Interpréter géométriquement l'intégrale $I_n$.
   2. En utilisant cette interprétation, formuler une conjecture sur le sens de variation de la suite $\left (I_n\right )$ et sa limite éventuelle. On précisera les éléments sur lesquels on s'appuie pour conjecturer.
2. Démontrer que pour tout entier naturel $n$ supérieur ou égal à 1, $$I_{n+1} -I_n =\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x$$ En déduire le signe de $I_{n+1} -I_n $ puis démontrer que la suite $\left (I_n\right )$ est convergente.
3. Déterminer l'expression de $I_n$ en fonction de $n$ et déterminer la limite de la suite $\left (I_n\right )$.