Baccalauréat S Centres étrangers 12 juin 2014
Dans l'ensemble du sujet, et pour chaque question, toute trace de recherche même incomplète, ou d'initiative même non fructueuse, sera prise en compte dans l'évaluation.
Exercice 1 4 points
Cet exercice est un questionnaire à choix multiples comportant quatre questions indépendantes. Pour chaque question, une seule des quatre affirmations proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à l'affirmation exacte. Aucune justification n'est demandée. Une réponse exacte rapporte un point ; une réponse fausse ou une absence de réponse ne rapporte ni n'enlève de point.
Question 1 Dans un hypermarché, 75 % des clients sont des femmes.
Une femme sur cinq achète un article au rayon bricolage, alors que sept hommes sur dix le font. Une personne, choisie au hasard, a fait un achat au rayon bricolage.
La probabilité que cette personne soit une femme a pour valeur arrondie au millième :
- 0,750
- 0,150
- 0,462
- 0,700
Question 2 Dans cet hypermarché, un modèle d'ordinateur est en promotion.
Une étude statistique a permis d'établir que, chaque fois qu'un client s'intéresse à ce modèle, la probabilité qu'il l'achète est égale à $0,3$.
On considère un échantillon aléatoire de dix clients qui se sont intéressés à ce modèle.
La probabilité qu'exactement trois d'entre eux aient acheté un ordinateur de ce modèle a pour valeur arrondie au millième :
- 0,900
- 0,092
- 0,00
- 0,267
Question 3 Cet hypermarché vend des téléviseurs dont la durée de vie, exprimée en année, peut être modélisée par une variable aléatoire réelle qui suit une loi exponentielle de paramètre $\lambda$.
La durée de vie moyenne d'un téléviseur est de huit ans, ce qui se traduit par : $\lambda = \dfrac{1}{8}$.
La probabilité qu'un téléviseur pris au hasard fonctionne encore au bout de six ans a pour valeur arrondie au millième :
- 0,750
- 0,250
- 0,472
- 0,528
Question 4 Cet hypermarché vend des baguettes de pain dont la masse, exprimée en gramme, est une variable aléatoire réelle qui suit une loi normale de moyenne $200$~g.
La probabilité que la masse d'une baguette soit comprise entre 184 g et 216 g est égale à $0,954$.
La probabilité qu'une baguette prise au hasard ait une masse inférieure à 192 g a pour valeur arrondie au centième :
- 0,16
- 0,32
- 0,84
- 0,48
Exercice 1 4 points
Aucune justification n'est demandée. Une réponse exacte rapporte un point ; une réponse fausse ou une absence de réponse ne rapporte ni n'enlève de point.
Une femme sur cinq achète un article au rayon bricolage, alors que sept hommes sur dix le font. Une personne, choisie au hasard, a fait un achat au rayon bricolage.
La probabilité que cette personne soit une femme a pour valeur arrondie au millième :
- 0,750
- 0,150
- 0,462
- 0,700
On appelle $F$ l’événement la personne est une femme et $B$ l’événement la personne achète un article au rayon bricolage. On obtient alors l’arbre suivant : 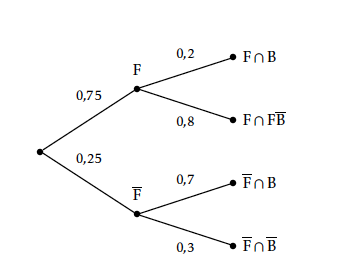
Par conséquent, d’après la propriété des probabilités totales, on a : $$\begin{array} p(B) &=p(B \cap F) + p\left(B \cap \bar{F} \right) \\\\ &= 0,75 \times 0,2 + 0,25 \times 0,7 \\\\ & = 0,325 \end{array}$$ On cherche à connaître : $$\begin{array} p_B(F) &= \dfrac{p(B \cap F)}{p(B)} \\\\ &= \dfrac{0,75 \times 0,2}{0,325} \\\\ &\approx 0,462 \end{array}$$
Réponse c
Une étude statistique a permis d'établir que, chaque fois qu'un client s'intéresse à ce modèle, la probabilité qu'il l'achète est égale à $0,3$.
On considère un échantillon aléatoire de dix clients qui se sont intéressés à ce modèle.
La probabilité qu'exactement trois d'entre eux aient acheté un ordinateur de ce modèle a pour valeur arrondie au millième :
- 0,900
- 0,092
- 0,00
- 0,267
On appelle $X$ la variable aléatoire qui compte le nombre de clients ayant acheté un ordinateur de ce modèle.
Il y a 10 « tirages », tous identiques, aléatoires et indépendants.
Chaque tirage ne possède que 2 issues : $A$ « le client a acheté un ordinateur » de probabilité $p(A)=0,3$ et $\overline{A}$ ...
La variable aléatoire $X$ suit donc la loi binomiale $\mathcal{B}(10;0,3)$. Donc $P(X=3)=\binom{10}{3} \times 0,3 ^3\times 0,7^7 \approx 0,267$
Réponse d
La durée de vie moyenne d'un téléviseur est de huit ans, ce qui se traduit par : $\lambda = \dfrac{1}{8}$.
La probabilité qu'un téléviseur pris au hasard fonctionne encore au bout de six ans a pour valeur arrondie au millième :
- 0,750
- 0,250
- 0,472
- 0,528
On appelle $T $ la variable aléatoire suivant la loi exponentielle de paramètres $\lambda=18$.
On calcule donc $$P(T\geq 6)=e^{−6\lambda} \approx 0,472 $$
Réponse c.
La probabilité que la masse d'une baguette soit comprise entre 184 g et 216 g est égale à $0,954$.
La probabilité qu'une baguette prise au hasard ait une masse inférieure à 192 g a pour valeur arrondie au centième :
- 0,16
- 0,32
- 0,84
- 0,48
On appelle $Y$ la variable aléatoire suivant la loi normale $\mathcal{N}(200;\sigma^2).$
D’après le cours on sait que $P(200−2\sigma \leq Y\leq 200+2\sigma )=0,954.$
Or ici on sait que $P(184\leq Y\leq 216)=0,954.$
Par conséquent $2\sigma =16$ soit $\sigma =8$
On en déduit donc que $P(Y\leq 192)=0,5–P(192\leq Y\leq 200) \approx 0,16.$
Réponse a
Exercice 2 4 points
On définit, pour tout entier naturel $n$, les nombres complexes $z$ par : \[\left\{\begin{array}{l c l} z_{0}&=& 16\\ z_{n+1}&=&\dfrac{1 + \text{i}}{2}z_{n},\: \text{pour tout entier naturel} \: n. \end{array}\right.\] On note $r_{n}$ le module du nombre complexe $z_{n}\: : r_{n} =\left|z_{n}\right|$. Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.
- Calculer $z_{1}, z_{2}$ et $z_{3}$.
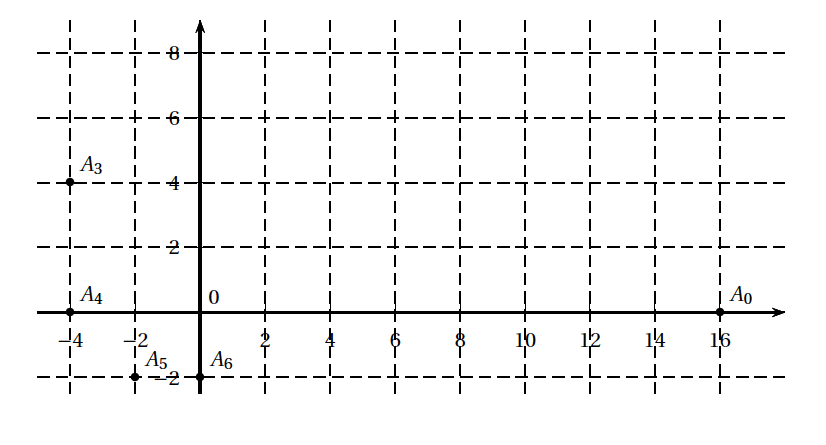
- Placer les points $A_{1}$ et $A_{2}$ sur le graphique de l' annexe, à rendre avec la copie .
- Écrire le nombre complexe $\dfrac{1 + \text{i}}{2}$ sous forme trigonométrique.
- Démontrer que le triangle O$A_{0}A_{1}$ est isocèle rectangle en $A_{1}$.
- Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$. La suite $\left(r_{n}\right)$ est-elle convergente ? Interpréter géométriquement le résultat précédent. On note $L_{n}$ la longueur de la ligne brisée qui relie le point $A_{0}$ au point $A_{n}$ en passant successivement par les points $A_{1}, A_{2}, A_{3}$, etc. Ainsi $L_{n} = \displaystyle\sum_{i=0}^{n-1} A_{i}A_{i+1} = A_{0}A_{1} + A_{1}A_{2} + \ldots + A_{n-1}A_{n}.$
- Démontrer que pour tout entier naturel $n \::\: A_{n}A_{n+1} = r_{n+1}$.
- Donner une expression de $L_{n}$ en fonction de $n$.
- Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$.
Exercice 2 4 points
On note $r_{n}$ le module du nombre complexe $z_{n}\: : r_{n} =\left|z_{n}\right|$. Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points $A_{n}$ d'affixes $z_{n}$.
- Calculer $z_{1}, z_{2}$ et $z_{3}$. $z_2 = \dfrac{1+\text{i}}{2}\times 8(1 + \text{i}) $ $=8i$
- $z_3 = \dfrac{1+\text{i}}{2}\times 8\text{i} = -4 + 4\text{i}$
- Placer les points $A_{1}$ et $A_{2}$ sur le graphique de l' annexe, à rendre avec la copie .
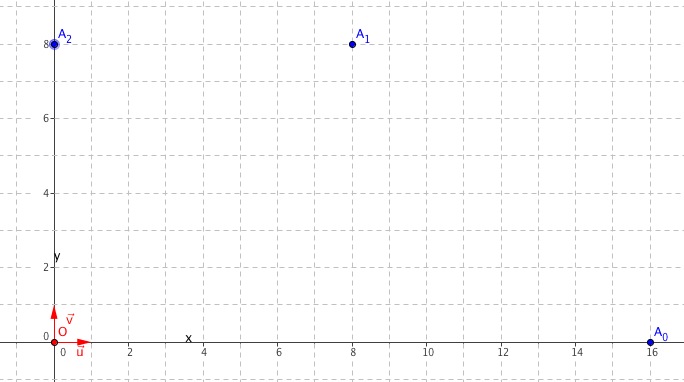
- Écrire le nombre complexe $\dfrac{1 + \text{i}}{2}$ sous forme trigonométrique. $\left| \dfrac{1+\text{i}}{2} \right| = \dfrac{\sqrt{2}}{2}$
- Donc $\dfrac{1+\text{i}}{2} = \dfrac{\sqrt{2}}{2} \left(\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2} \text{i} \right)$ $=\dfrac{\sqrt{2}}{2} \left( \cos \dfrac{\pi}{4} + \text{i} \sin \dfrac{\pi}{4} \right) $ $\quad \left(= \dfrac{\sqrt{2}}{2} \text{e}^{\text{i}\pi/4} \right)$
- Démontrer que le triangle O$A_{0}A_{1}$ est isocèle rectangle en $A_{1}$. $OA_1 = |z_1| = 8\sqrt{2}$
- $A_1A_0 = |z_0 – z_1| $ $=|8 – 8\text{i} | $ $=8\sqrt{2}$
- $OA_0 = |z_0| = 16$
- Le triangle $OA_0A_1$ est bien isocèle en $A_1$.
- De plus $16^2 = 2 \times \left( 8\sqrt{2} \right)^2$ donc $OA_0^2 = OA_1^2+A_1A_0^2$
- D’après la réciproque du théorème de Pythagore, le triangle est également rectangle en $A_1$.
- Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$. La suite $\left(r_{n}\right)$ est-elle convergente ? Interpréter géométriquement le résultat précédent. $$\begin{array}{ll} r_{n+1} &=|z_{n+1}| \\ & = \left| \dfrac{1+\text{i}}{2} \right| \times |z_n| \\ &=\dfrac{\sqrt{2}}{2} r_n\\ \end{array}$$ La suite $(r_n)$ est donc bien géométrique de raison $\dfrac{\sqrt{2}}{2}$.
- $0 < \dfrac{\sqrt{2}}{2}< 1$ donc $\lim\limits_{n \rightarrow +\infty} \left(\dfrac{\sqrt{2}}{2} \right)^n = 0$
- Par conséquent $\lim\limits_{n \rightarrow +\infty} r_n = 0$
- $~$
- Cela signifie donc que la distance $OA_n$ tend vers $0$ et que donc le point $A_n$ « se rapproche » de O.
- Démontrer que pour tout entier naturel $n \::\: A_{n}A_{n+1} = r_{n+1}$. $$ \begin{array} \\A_{n}A_{n+1} &= |z_{n+1}-z_n| \\ & = \left|\dfrac{1+\text{i}}{2}z_n -z_n \right| \\ & = \left|\dfrac{-1+\text{i}}{2}z_n \right| \\ &= \dfrac{\sqrt{2}}{2} |z_n| \\ &= r_{n+1} \end{array}$$
- Donner une expression de $L_{n}$ en fonction de $n$. On a donc :
- $$\begin{array}\\ L_{n}&= \sum_{i=0}^{i=n-1} r_{i+1} \\ & = r_1+r_2+\ldots+r_n \\ & = 8\sqrt{2} \dfrac{1-\left(\dfrac{\sqrt{2}}{2} \right) ^n}{1 - \dfrac{\sqrt{2}}{2}}\\ \end{array}$$
- On utilise la formule donnant la somme d’une suite géométrique :
- $$ 1^\text{er}\text{ terme} \times \dfrac{1 – \text{raison}^\text{nombre de termes}}{1 – \text{raison}}$$
- Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$. On a vu que $\lim\limits_{n \rightarrow +\infty} \left(\dfrac{\sqrt{2}}{2} \right)^n = 0$.
- Par conséquent $\lim\limits_{n \rightarrow +\infty} L_n = \dfrac{8\sqrt{2}}{1 - \dfrac{\sqrt{2}}{2}}$ $=16 + 16\sqrt{2}$
Exercice 3 7 points
Une image numérique en noir et blanc est composée de petits carrés (pixels) dont la couleur va du blanc au noir en passant par toutes les nuances de gris. Chaque nuance est codée par un réel $x$ de la façon suivante :
- $x = 0$ pour le blanc ;
- $x = 1$ pour le noir;
- $x = 0,01 \:;\: x = 0,02$ et ainsi de suite jusqu'à $x = 0,99$ par pas de $0,01$ pour toutes les nuances intermédiaires (du clair au foncé).
L'image A, ci-après, est composée de quatre pixels et donne un échantillon de ces nuances avec leurs codes. Un logiciel de retouche d'image utilise des fonctions numériques dites « fonctions de retouche » . Une fonction $f$ définie sur l'intervalle [0 ; 1] est dite « fonction de retouche » si elle possède les quatre propriétés suivantes :
- $f(0) = 0$ ;
- $f(1) = 1$ ;
- $f$ est continue sur l'intervalle [0 ; 1] ;
- $f$ est croissante sur l'intervalle [0 ; 1].
Une nuance codée $x$ est dite assombrie par la fonction $f$ si $f(x) > x$, et éclaircie, si $f(x) < x$. Ainsi, si $f(x) = x^2$, un pixel de nuance codée $0,2$ prendra la nuance codée $0,2^2 = 0,04$. L'image A sera transformée en l'image B ci-dessous. Si $f(x) = \sqrt{x}$, la nuance codée $0,2$ prendra la nuance codée $\sqrt{0,2} \approx 0,45$. L'image A sera transformée en l'image C ci-dessous.

Partie A
- On considère la fonction $f_{1}$ définie sur l'intervalle [0 ; 1] par : \[f_{1}(x) = 4x^3 - 6x^2 + 3x.\]
- Démontrer que la fonction $f_{1}$ est une fonction de retouche.
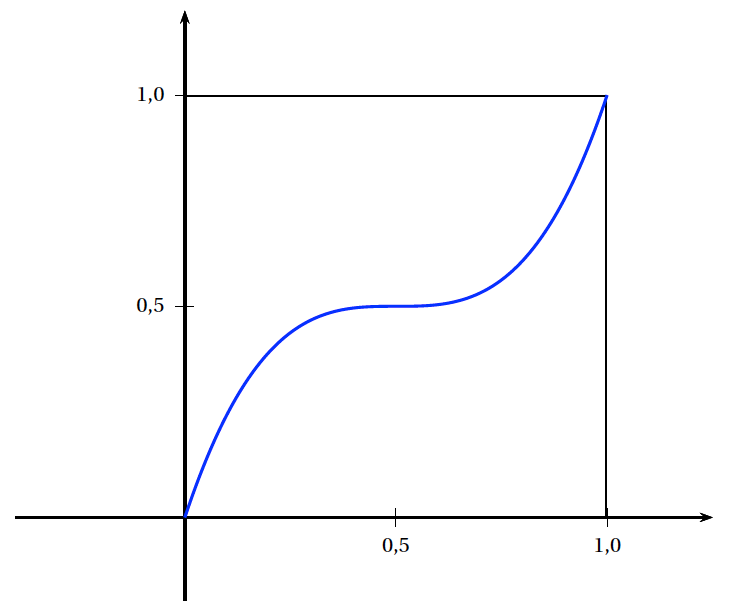
- Résoudre graphiquement l'inéquation $f_{1}(x) \leqslant x$, à l'aide du graphique donné en annexe, à rendre avec la copie, en faisant apparaître les pointillés utiles. Interpréter ce résultat en termes d'éclaircissement ou d'assombrissement.
- On considère la fonction $f_{2}$ définie sur l'intervalle [0 ; 1] par : \[f_{2}(x) = \ln [1 + (\text{e} - 1)x].\] On admet que $f_{2}$ est une fonction de retouche. On définit sur l'intervalle [0 ; 1] la fonction $g$ par : $g(x) = f_{2}(x) - x$.
- Établir que, pour tout $x$ de l'intervalle [0 ; 1] : $g'(x) = \dfrac{(\text{e} - 2) - (\text{e} - 1)x}{1 + (\text{e} - 1)x}$ ;
- Déterminer les variations de la fonction $g$ sur l'intervalle [0 ; 1]. Démontrer que la fonction $g$ admet un maximum en $\dfrac{\text{e} - 2}{\text{e} - 1}$, maximum dont une valeur arrondie au centième est $0,12$.
- Établir que l'équation $g(x) = 0,05$ admet sur l'intervalle [0 ; 1] deux solutions $\alpha$ et $\beta$, avec $\alpha < \beta$. On admettra que : $0,08 < \alpha < 0,09$ et que : $0,85 < \beta < 0,86$.
On remarque qu'une modification de nuance n'est perceptible visuellement que si la valeur absolue de l'écart entre le code de la nuance initiale et le code de la nuance modifiée est supérieure ou égale à $0,05$.
- Dans l'algorithme décrit ci-dessous, $f$ désigne une fonction de retouche. Quel est le rôle de cet algorithme ?
$$\begin{array}{ | l|l|} \hline \text{Variables :}& x \text{ (nuance initiale)}\\ &y \text{ (nuance retouchée) }\\ &E \text{ (écart)}\\ &c \text{ (compteur)}\\ & k\\ \text{Initialisation :}& c \text{ prend la valeur 0 }\\ \text{Traitement :}& \text{ Pour } k \text{ allant de 0 à 100, faire}\\ & \begin{array}{l|l l}\\ &x \text{ prend la valeur } \frac{k}{100}&\\ &y \text{ prend la valeur } f(x)& \\ &E \text{ prend la valeur } |y - x|&\\ &&\begin{array}{l| l } &\text{ Si } E > \text{0,05, faire } \\ & \quad c \text{ prend la valeur } c + 1\\ & \text{ Fin si } \end{array} \end{array} \\ &\text{ Fin pour }\\ \text{Sortie :}& \text{ Afficher } c \\ \hline \end{array}$$
L’algorithme calcule le nombre de nuances pour lesquelles la modification de nuances est perceptible visuellement.
- Quelle valeur affichera cet algorithme si on l'applique à la fonction $f_{2}$ définie dans la deuxième question de la Partie A ?
Partie C
Dans cette partie, on s'intéresse à des fonctions de retouche $f$ dont l'effet est d'éclaircir l'image dans sa globalité, c'est-a-dire telles que, pour tout réel $x$ de l'intervalle [0 ; 1], $f(x) \leqslant x$.
On décide de mesurer l'éclaircissement global de l'image en calculant l'aire $\mathcal{A}_{f}$ de la portion de plan comprise entre l'axe des abscisses, la courbe représentative de la fonction $f$, et les droites d'équations respectives $x = 0$ et $x = 1$. Entre deux fonctions, celle qui aura pour effet d'éclaircir le plus l'image celle correspondant à la plus petite aire.
On désire comparer l'effet des deux fonctions suivantes, dont on admet qu'elles sont des fonctions de retouche :
\[f_{1}(x) = x \text{e}^{\left(x^2 - 1 \right)}\qquad f_{2}(x) = 4x - 15 + \dfrac{60}{x+4}.\]
- Calculer $\mathcal{A}_{f_{1}}$.
- Calculer $\mathcal{A}_{f_{2}}$
- De ces deux fonctions, laquelle a pour effet d'éclaircir le plus l'image ?
Exercice 3 7 points
- $x = 0$ pour le blanc ;
- $x = 1$ pour le noir;
- $x = 0,01 \:;\: x = 0,02$ et ainsi de suite jusqu'à $x = 0,99$ par pas de $0,01$ pour toutes les nuances intermédiaires (du clair au foncé).
L'image A, ci-après, est composée de quatre pixels et donne un échantillon de ces nuances avec leurs codes. Un logiciel de retouche d'image utilise des fonctions numériques dites « fonctions de retouche » . Une fonction $f$ définie sur l'intervalle [0 ; 1] est dite « fonction de retouche » si elle possède les quatre propriétés suivantes :
- $f(0) = 0$ ;
- $f(1) = 1$ ;
- $f$ est continue sur l'intervalle [0 ; 1] ;
- $f$ est croissante sur l'intervalle [0 ; 1].
Une nuance codée $x$ est dite assombrie par la fonction $f$ si $f(x) > x$, et éclaircie, si $f(x) < x$. Ainsi, si $f(x) = x^2$, un pixel de nuance codée $0,2$ prendra la nuance codée $0,2^2 = 0,04$. L'image A sera transformée en l'image B ci-dessous. Si $f(x) = \sqrt{x}$, la nuance codée $0,2$ prendra la nuance codée $\sqrt{0,2} \approx 0,45$. L'image A sera transformée en l'image C ci-dessous.

Partie A
- On considère la fonction $f_{1}$ définie sur l'intervalle [0 ; 1] par : \[f_{1}(x) = 4x^3 - 6x^2 + 3x.\]
- Démontrer que la fonction $f_{1}$ est une fonction de retouche. $f_1(0) = 4\times 0^3 – 6\times 0^2 + 3\times 0 = 0$
- $f_1(1) = 4 – 6 + 3 = 1$
- $f_1$ est un polynôme. Elle est donc continue et dérivable sur $[0;1]$.
- $f_1′(x) = 12x^2-12x+3 = 3(4^2-4x+1)$ $=3(2x-1)^2 \ge 0$
- Donc $f_1$ est croissante sur $[0;1]$.
- $f_1$ est bien une fonction de retouche.
- Résoudre graphiquement l'inéquation $f_{1}(x) \leqslant x$, à l'aide du graphique donné en annexe, à rendre avec la copie, en faisant apparaître les pointillés utiles. Interpréter ce résultat en termes d'éclaircissement ou d'assombrissement.

- L'ensemble des solutions de $f_1(x) \le x$ est donc, graphiquement, $[0,5;1]\cup{0}$.
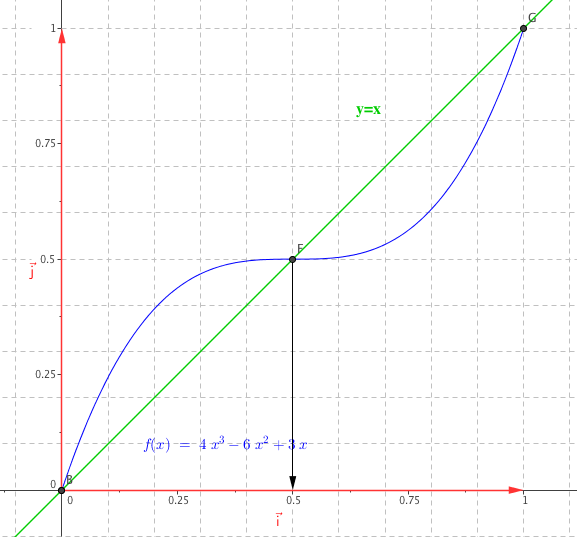
- Cela signifie donc que la fonction $f_1$ assombrit les nuances inférieures à $0,5$ et éclaircit celles supérieures à $0,5$.
- On considère la fonction $f_{2}$ définie sur l'intervalle [0 ; 1] par : \[f_{2}(x) = \ln [1 + (\text{e} - 1)x].\] On admet que $f_{2}$ est une fonction de retouche. On définit sur l'intervalle [0 ; 1] la fonction $g$ par : $g(x) = f_{2}(x) - x$.
- Établir que, pour tout $x$ de l'intervalle [0 ; 1] : $g'(x) = \dfrac{(\text{e} - 2) - (\text{e} - 1)x}{1 + (\text{e} - 1)x}$ ; $$\begin{array}\\ g’(x) &= f_2′(x) – 1 \\ &=\dfrac{\text{e} – 1}{1 + (\text{e} – 1)x} – 1 \\ &=\dfrac{\text{e} – 1 – 1 – (\text{e} – 1)x}{1 + (\text{e} – 1)x} \\ &=\dfrac{(\text{e} – 2) - (\text{e} – 1)x}{1 + (\text{e} – 1)x} \end{array}$$
- Déterminer les variations de la fonction $g$ sur l'intervalle [0 ; 1]. Démontrer que la fonction $g$ admet un maximum en $\dfrac{\text{e} - 2}{\text{e} - 1}$, maximum dont une valeur arrondie au centième est $0,12$. Pour tout $x \in [0;1] 0 \le 1 + (\text{e}-1)x$
- Donc le signe de $g’(x)$ ne dépend que de celui du numérateur.
- $$\begin{array} (\text{e} – 2) - (\text{e} – 1)x \ge 0 & \Leftrightarrow (\text{e} – 2) \ge (\text{e} – 1)x \\ & \Leftrightarrow x \le \dfrac{(\text{e} – 2)}{(\text{e} – 1)} = \alpha \end{array}$$
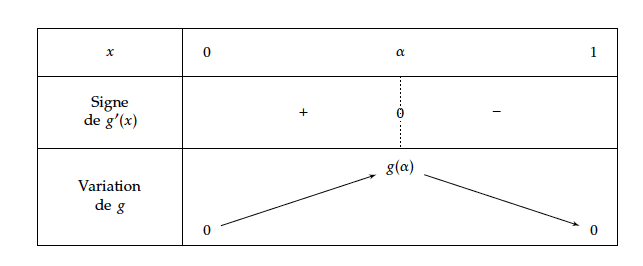
- et $g(\alpha) \approx 0,12$
- La fonction $g$ admet donc un maximum en $\alpha$
- Établir que l'équation $g(x) = 0,05$ admet sur l'intervalle [0 ; 1] deux solutions $\alpha$ et $\beta$, avec $\alpha < \beta$. On admettra que : $0,08 < \alpha < 0,09$ et que : $0,85 < \beta < 0,86$.
La fonction $g$ est continue et strictement croissante sur $[0;\alpha]$.
- $g(0) = 0$ et $g(\alpha) \approx 0,12$
- Par conséquent $0,05 \in [0;0,12]$.
- D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $g(x) = 0,05$ possède une unique solution sur $[0;\alpha]$.$~$
- La fonction $g$ est continue et strictement décroissante sur $[\alpha;1]$.
- $g(1) = 0$ et $g(\alpha) \approx 0,12$
- Par conséquent $0,05 \in [0;0,12]$.
- D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $g(x) = 0,05$ possède une unique solution sur $[0;\alpha]$.$~$
- Par conséquent l’équation $g(x) = 0$ possède bien deux solutions
- $g(0,08) \approx 0,049$ et $g(0,09) \approx 0,054$
- Donc la première solution est bien comprise entre $0,08$ et $0,09$.
- $~$
- $g(0,85) \approx 0,0504$ et $g(0,86) \approx 0,0473$
- donc la deuxième solution est bien comprise entre $0,85$ et $0,86$.
On remarque qu'une modification de nuance n'est perceptible visuellement que si la valeur absolue de l'écart entre le code de la nuance initiale et le code de la nuance modifiée est supérieure ou égale à $0,05$.
- Dans l'algorithme décrit ci-dessous, $f$ désigne une fonction de retouche. Quel est le rôle de cet algorithme ? $$\begin{array}{ | l|l|} \hline \text{Variables :}& x \text{ (nuance initiale)}\\ &y \text{ (nuance retouchée) }\\ &E \text{ (écart)}\\ &c \text{ (compteur)}\\ & k\\ \text{Initialisation :}& c \text{ prend la valeur 0 }\\ \text{Traitement :}& \text{ Pour } k \text{ allant de 0 à 100, faire}\\ & \begin{array}{l|l l}\\ &x \text{ prend la valeur } \frac{k}{100}&\\ &y \text{ prend la valeur } f(x)& \\ &E \text{ prend la valeur } |y - x|&\\ &&\begin{array}{l| l } &\text{ Si } E > \text{0,05, faire } \\ & \quad c \text{ prend la valeur } c + 1\\ & \text{ Fin si } \end{array} \end{array} \\ &\text{ Fin pour }\\ \text{Sortie :}& \text{ Afficher } c \\ \hline \end{array}$$
- Quelle valeur affichera cet algorithme si on l'applique à la fonction $f_{2}$ définie dans la deuxième question de la Partie A ? On cherche donc les valeurs de $x$ telles que $f_2(x) – x \ge 0,05$ c’est-à-dire $g(x) \ge 0,05$.
- Ce sont donc toutes les nuances comprises entre les $2$ solutions $\alpha$ et $\beta$ de la partie précédente.
- On va donc prendre toutes les nuances comprises entre $0,09$ et $0,85$. Il y en a par conséquent $85 – 9 + 1 = 77$.
- $~$
- L’algorithme affichera donc $77$.
Dans cette partie, on s'intéresse à des fonctions de retouche $f$ dont l'effet est d'éclaircir l'image dans sa globalité, c'est-a-dire telles que, pour tout réel $x$ de l'intervalle [0 ; 1], $f(x) \leqslant x$.
On décide de mesurer l'éclaircissement global de l'image en calculant l'aire $\mathcal{A}_{f}$ de la portion de plan comprise entre l'axe des abscisses, la courbe représentative de la fonction $f$, et les droites d'équations respectives $x = 0$ et $x = 1$. Entre deux fonctions, celle qui aura pour effet d'éclaircir le plus l'image celle correspondant à la plus petite aire.
On désire comparer l'effet des deux fonctions suivantes, dont on admet qu'elles sont des fonctions de retouche :

\[f_{1}(x) = x \text{e}^{\left(x^2 - 1 \right)}\qquad f_{2}(x) = 4x - 15 + \dfrac{60}{x+4}.\]
- Calculer $\mathcal{A}_{f_{1}}$. $\mathcal{A_{f_1}} = \displaystyle \int_0^1 f_1(x)\text{d}x $.
- Une primitive de $f_1$ est $F_1$ définie par $F_1(x) = 0,5\text{e}^{x^2-1}$
- Donc $\mathcal{A_{f_1}} = F_1(1) – F_1(0) = 0,5 – 0,5\text{e}^{-1}$ u.a. $\approx 0,316$
- Calculer $\mathcal{A}_{f_{2}}$ $\mathcal{A_{f_2}} = \displaystyle \int_0^1 f_2(x)\text{d}x $.
- Une primitive de $f_2$ est $F_2$ définie par $F_2(x) =2x^2-15x+60\ln (x+4)$
- Donc $\mathcal{A_{f_2}} = F_2(1) – F_2(0) = -13 +60 \ln 5 – 60 \ln(4) $ u.a. $\approx 0,389$
- De ces deux fonctions, laquelle a pour effet d'éclaircir le plus l'image ? La fonction $f_1$ a donc l’aire la plus petite. C’est elle qui aura pour effet d’éclaircir le plus l’image.
Exercice 4 5 points
Dans l'espace muni d'un repère orthonormé, on considère les points : \[\text{A}(1 ; 2 ; 7),\quad \text{B}(2 ; 0 ; 2),\quad \text{C}(3 ; 1 ; 3),\quad \text{D}(3 ; -6 ; 1) \:\:\text{et E}(4 ; -8 ; -4).\]
- Montrer que les points A, B et C ne sont pas alignés.
- Soit $\vec{u}(1 ; b ; c)$ un vecteur de l'espace, où $b$ et $c$ désignent deux nombres réels.
- Déterminer les valeurs de $b$ et $c$ telles que $\vec{u}$ soit un vecteur normal au plan (ABC).
- En déduire qu'une équation cartésienne du plan (ABC) est : $x - 2 y + z - 4 = 0$.
- Le point D appartient-il au plan (ABC) ?
- On considère la droite $\mathcal{D}$ de l'espace dont une représentation paramétrique est : \[\left\{\begin{array}{l c l} x& =& \phantom{-}2t+3\\ y& =& - 4t + 5\\ z& =&\phantom{-}2t-1 \end{array}\right. \: \text{où}\: t\: \text{est un nombre réel.}\]
- La droite $\mathcal{D}$ est-elle orthogonale au plan (ABC) ?
- Déterminer les coordonnées du point H, intersection de la droite $\mathcal{D}$ et du plan (ABC).
- Étudier la position de la droite (DE) par rapport au plan (ABC).
Exercice 4 5 points
\[\text{A}(1 ; 2 ; 7),\quad \text{B}(2 ; 0 ; 2),\quad \text{C}(3 ; 1 ; 3),\quad \text{D}(3 ; -6 ; 1) \:\:\text{et E}(4 ; -8 ; -4).\]
- Montrer que les points A, B et C ne sont pas alignés. $\vec{AB} = (1;-2;-5)$ et $\vec{AC}(2;-1;-4)$.
- Les $2$ vecteurs ne sont pas colinéaires par conséquent les points $A$, $B$ et$ C$ ne sont pas alignés.
- Soit $\vec{u}(1 ; b ; c)$ un vecteur de l'espace, où $b$ et $c$ désignent deux nombres réels.
- Déterminer les valeurs de $b$ et $c$ telles que $\vec{u}$ soit un vecteur normal au plan (ABC). On veut donc que :
- $$\begin {array}{ll} \begin{cases} \vec{u}.\vec{AB} = 0 \\ \vec{u}.\vec{AC} = 0 \end{cases} & \Leftrightarrow \begin{cases} 1- 2b- 5c = 0 \\2 -b-4c = 0 \end{cases} \\ & \Leftrightarrow \begin{cases} b= 2-4c \\-2(2-4c)-5c=-1 \end{cases}\\ & \Leftrightarrow \begin{cases} b=2-4c \\3c=3 \end{cases} \\ & \Leftrightarrow \begin{cases} c=1 \\b= -2 \end{cases} \end{array}$$ Donc $\vec{u}(1,-2,1)$.
- En déduire qu'une équation cartésienne du plan (ABC) est : $x - 2 y + z - 4 = 0$. Une équation cartésienne du plan $(ABC)$ est alors de la forme :
- $$x-2y+z+d=0$$
- Or $A$ appartient au plan $ABC$ donc :
- $$1 -4 + 7 +d = 0 \Leftrightarrow d = -4$$
- Une équation cartésienne de $(ABC)$ est donc bien $x-2y+z-4=0$
- Le point D appartient-il au plan (ABC) ? Regardons si les coordonnées du point $D$ vérifient l’équation précédente :
- $$3 + 12 + 1 – 4 = 12 \ne 0$$
- Donc $D$ n’appartient pas à $(ABC)$.
- On considère la droite $\mathcal{D}$ de l'espace dont une représentation paramétrique est : \[\left\{\begin{array}{l c l} x& =& \phantom{-}2t+3\\ y& =& - 4t + 5\\ z& =&\phantom{-}2t-1 \end{array}\right. \: \text{où}\: t\: \text{est un nombre réel.}\]
- La droite $\mathcal{D}$ est-elle orthogonale au plan (ABC) ? Un vecteur directeur de $\mathscr{D}$ est $\vec{v}(2;-4;2) = 2\vec{u}$.
- Donc $\mathscr{D}$ est orthogonale au plan $(ABC)$.
- Déterminer les coordonnées du point H, intersection de la droite $\mathcal{D}$ et du plan (ABC). Pour trouver les coordonnées du point d’intersection de la droite et du plan on va injecter dans l’équation du plan les équations paramétriques de la droite.
- $$\begin{array} 2t+3 -2(-4t+5)+(2t-1)-4 = 0 &\Leftrightarrow 2t+3+8t-10+2t-1-4=0 \\\\
- & \Leftrightarrow 12t-12=0 \\ &\Leftrightarrow t = 1 \end{array}$$ Le point $H$ a donc pour coordonnées $(5;1;1)$
- Étudier la position de la droite (DE) par rapport au plan (ABC). $\vec{DE}(1;-2;-5)$. Ce vecteur n’est pas colinéaire $ \vec{u}$ donc la droite $(DE)$ n’est pas orthogonale au plan $(ABC)$.
- $\vec{DE}.\vec{u} = 1 +4 – 5 = 0$.
- Donc la droite $(DE)$ est pas parallèle au plan $(ABC)$.
- Puisque $D$ n’appartient pas à $(ABC)$ alors la droite est strictement parallèle au plan.
Spécialité 5 points
Partie A : préliminaires
- Soient $n$ et $N$ deux entiers naturels supérieurs ou égaux à 2, tels que : \[n^2 \equiv N -1\quad \text{modulo}\: N.\] Montrer que : $n \times n^3 \equiv 1 \quad \text{modulo}\:\: N$.
- Déduire de la question précédente un entier $k_{1}$ tel que: $5k_{1} \equiv 1\quad \text{modulo}\:\: 26$. On admettra que l'unique entier $k$ tel que : $ 0 \leqslant k \leqslant 25$ et $5k \equiv 1 \quad \text{modulo}\:\: 26$ vaut 21.
- On donne les matrices : $A = \begin{pmatrix}4&1\\3&2\end{pmatrix},\: B = \begin{pmatrix}2&- 1\\- 3&4\end{pmatrix},\: X = \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ et $Y = \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$.
- Calculer la matrice $6A - A^2$.
- En déduire que $A$ est inversible et que sa matrice inverse, notée $A^{- 1}$, peut s'écrire sous la forme $A^{-1} = \alpha I + \beta A$, ou $\alpha$ et $\beta$ sont deux réels que l'on déterminera.
- Vérifier que : $B = 5A^{-1}$.
- Démontrer que si $A X = Y$, alors $5X = B Y$.
Partie B : procédure de codage
Coder le mot « ET » , en utilisant la procédure de codage décrite ci-dessous.
- Le mot à coder est remplacé par la matrice $X = \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$, où $x_{1}$ est l'entier représentant la première lettre du mot et $x_{2}$ l'entier représentant la deuxième, selon le tableau de correspondance ci-dessous : $$\begin{array}{}\hline A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12\\ \hline \hline N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\ \hline 13&14&15&16&17&18&19&20&21&22&23&24&25\\ \hline \end{array}$$
- La matrice $X$ est transformée en la matrice $Y = \begin{pmatrix}y_{1}\\ y_{2} \end{pmatrix}$ telle que : $Y = AX$.
- La matrice $Y$ est transformée en la matrice $R = \begin{pmatrix}r_{1}\\r_{2}\end{pmatrix}$, où $r_{1}$ est le reste de la division euclidienne de $y_{1}$ par 26 et $r_{2}$ le reste de la division euclidienne de $y_{2}$ par 26.
- Les entiers $r_{1}$ et $r_{2}$ donnent les lettres du mot codé, selon le tableau de correspondance ci-dessus.
Exemple : « OU » (mot à coder) $\to X \begin{pmatrix}14\\20\end{pmatrix} \to Y = \begin{pmatrix}76\\82\end{pmatrix} \to R = \begin{pmatrix}24\\4 \end{pmatrix} \to $ « YE » (mot codé).
Partie C : procédure de décodage
(on conserve les mêmes notations que pour le codage) Lors du codage, la matrice $X$ a été transformée en la matrice $Y = \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ telle que : $Y = A X$.
- Démontrer que : $\left\{\begin{array}{l c l} 5x_{1} &=& \phantom{-}2y_{1} - y_{2}\\ 5x_{2} &=&- 3y_{1} + 4y_{2} \end{array}\right..$
- En utilisant la question 1. b. de la \textbf{partie A}, établir que: \[\left\{\begin{array}{l c l} x_{1}&\equiv&16y_{1} + 5y_{2}\\ x_{2}&\equiv&15y_{1} + 6y_{2} \end{array}\right. \quad \text{modulo}\:\: 26\]
- Décoder le mot « QP » .
Spécialité 5 points
Partie A : préliminaires
- Soient $n$ et $N$ deux entiers naturels supérieurs ou égaux à 2, tels que : \[n^2 \equiv N -1\quad \text{modulo}\: N.\] Montrer que : $n \times n^3 \equiv 1 \quad \text{modulo}\:\: N$. $n \times n^3 = \left(n^2 \right)^2 \equiv (N-1)^2 [N]$
- Or $(N-1)^2 = N^2 - 2N + 1 \equiv 1 [N]$
- Donc $n \times n^3 \equiv 1 [N]$
- Déduire de la question précédente un entier $k_{1}$ tel que: $5k_{1} \equiv 1\quad \text{modulo}\:\: 26$. On admettra que l'unique entier $k$ tel que : $ 0 \leqslant k \leqslant 25$ et $5k \equiv 1 \quad \text{modulo}\:\: 26$ vaut 21. $5^2 = 25 \equiv 26 - 1 [26]$
- Donc $5 \times 5^3\equiv 1 [26]$
- par conséquent $k_1 = 5^3= 125$
- On donne les matrices : $A = \begin{pmatrix}4&1\\3&2\end{pmatrix},\: B = \begin{pmatrix}2&- 1\\- 3&4\end{pmatrix},\: X = \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$ et $Y = \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$.
- Calculer la matrice $6A - A^2$. $A^2 = \begin{pmatrix}19&6 \\18&7 \end{pmatrix}$
- Donc $6A - A^2 = \begin{pmatrix} 5&0 \\0&5 \end{pmatrix}$ $=5I$
- En déduire que $A$ est inversible et que sa matrice inverse, notée $A^{- 1}$, peut s'écrire sous la forme $A^{-1} = \alpha I + \beta A$, ou $\alpha$ et $\beta$ sont deux réels que l'on déterminera. On a donc $ A(6I - A) = 5I$
- La matrice $A$ est donc inversible, d’inverse $A^{-1} =\dfrac{1}{5}(6I - A)$
- Vérifier que : $B = 5A^{-1}$. $6I - A = \begin{pmatrix} 2&-1\\-3&4 \end{pmatrix}$
- Donc $B = 5A^{-1}$.
- Démontrer que si $A X = Y$, alors $5X = B Y$. $$ \begin{array} AX=Y & \Leftrightarrow X=A^{-1}Y\\ & \Leftrightarrow X = \dfrac{1}{5}BY\\ &\Leftrightarrow 5X = BY \end{array} $$
Coder le mot « ET » , en utilisant la procédure de codage décrite ci-dessous.
- Le mot à coder est remplacé par la matrice $X = \begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$, où $x_{1}$ est l'entier représentant la première lettre du mot et $x_{2}$ l'entier représentant la deuxième, selon le tableau de correspondance ci-dessous : $$\begin{array}{}\hline A&B&C&D&E&F&G&H&I&J&K&L&M\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12\\ \hline \hline N&O&P&Q&R&S&T&U&V&W&X&Y&Z\\ \hline 13&14&15&16&17&18&19&20&21&22&23&24&25\\ \hline \end{array}$$
- La matrice $X$ est transformée en la matrice $Y = \begin{pmatrix}y_{1}\\ y_{2} \end{pmatrix}$ telle que : $Y = AX$.
- La matrice $Y$ est transformée en la matrice $R = \begin{pmatrix}r_{1}\\r_{2}\end{pmatrix}$, où $r_{1}$ est le reste de la division euclidienne de $y_{1}$ par 26 et $r_{2}$ le reste de la division euclidienne de $y_{2}$ par 26.
- Les entiers $r_{1}$ et $r_{2}$ donnent les lettres du mot codé, selon le tableau de correspondance ci-dessus.
Exemple : « OU » (mot à coder) $\to X \begin{pmatrix}14\\20\end{pmatrix} \to Y = \begin{pmatrix}76\\82\end{pmatrix} \to R = \begin{pmatrix}24\\4 \end{pmatrix} \to $ « YE » (mot codé).
« ET » est remplacé par $X = \begin{pmatrix} 4\\19 \end{pmatrix} $
Donc $Y = AX = \begin{pmatrix} 35\\50 \end{pmatrix}$
Par conséquent $R = \begin{pmatrix} 9\\24 \end{pmatrix}$
Donc « ET » est codé par « JY »
Partie C : procédure de décodage
(on conserve les mêmes notations que pour le codage) Lors du codage, la matrice $X$ a été transformée en la matrice $Y = \begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}$ telle que : $Y = A X$.
- Démontrer que : $\left\{\begin{array}{l c l} 5x_{1} &=& \phantom{-}2y_{1} - y_{2}\\ 5x_{2} &=&- 3y_{1} + 4y_{2} \end{array}\right..$
- En utilisant la question 1. b. de la \textbf{partie A}, établir que: \[\left\{\begin{array}{l c l} x_{1}&\equiv&16y_{1} + 5y_{2}\\ x_{2}&\equiv&15y_{1} + 6y_{2} \end{array}\right. \quad \text{modulo}\:\: 26\] D’après la question 1.b de la partie A on a $5 \times 21 \equiv 1 [26]$
- $$\begin{array} Y = AX & \Leftrightarrow X = A^{-1}Y\\ &\Leftrightarrow 5X = BY\\ &\Leftrightarrow \begin{cases} 5x_1=2y_1-y_2\\5x_2=-3y_1+4y_2 \end{cases} \end{array}$$
- Donc en multipliant les $2$ lignes du système précédent par $21$ on obtient :
- $$\begin{cases} 21 \times 5x_1=42y_1- 21y_2\\21 \times 5x_2=-63y_1+84y_2 \end{cases} \Leftrightarrow \begin{cases} x_1 \equiv 16y_1+5y_2 [26]\\x_2 \equiv 15y_1+6y_2 [26] \end{cases}$$
- Décoder le mot « QP » . « QP » est associé à $\begin{pmatrix} 16\\15 \end{pmatrix}$
- Donc $$\begin{cases} x_1 \equiv 16y_1+5y_2 [26]\\x_2 \equiv 15y_1+6y_2 [26] \end{cases} \Leftrightarrow \begin{cases} x_1 \equiv 331 [26]\\x_2 \equiv 330 [26] \end{cases} \Leftrightarrow \begin{cases} x_1 = 19\\x_2 = 18 \end{cases}$$
- Le mot de départ est donc « TS »
Spécialité 5 points
Annexe relative à l'exercice 2
Annexe relative à l'exercice 3
- Vues: 40611
