Baccalauréat STI2D–STL spécialité SPCL Polynésie - 11 juin 2015 - Correction Exercice 3

Page 6 sur 8: Correction Exercice 3

Correction de l'exercice 3 (6 points)

Fonctions

Exercice 3 6 points

Fonctions

Un pont à une seule arche d'une longueur de 16 m enjambe une route à double circulation. La figure ci-dessous donne une vue de l'une des deux façades de ce pont (1 unité représente 1 mètre). La partie supérieure du pont est à une hauteur de 5 m au-dessus de la route.
La partie de l'axe des abscisses comprise entre -8 et 8 représente la chaussée sur laquelle sont délimitées les zones de circulation des piétons, des cyclistes et des véhicules motorisés.

A-- Étude de la fonction représentée par la courbe $(\mathcal{C})$

Soit la fonction $f$ définie, pour tout réel $x$ de l'intervalle $[-8~;~8]$, par \[f(x) = k - 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\quad \text{où $k$ désigne un entier naturel fixé.}\] On note $(\mathcal{C})$ sa courbe représentative, donnée ci-dessus dans le repère orthonormé (O, A, B).

1. Déterminer graphiquement $f(0)$. En déduire que pour tout réel $x$ de l'intervalle $[-8~;~8]$ : \[f(x) = 5 - 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right).\]
On lit $f(0)=5$ puisque le point $(0,5)$ est un point de la courbe $(\mathcal{C})$.
$$\begin{array}{rl} f(0)=4 & \iff k-0,5(e^0+e^0)=4\\ & \iff k-0,5(1+1)=4\\ & \iff k-1=4\\ & \iff k=5\\ \end{array}$$
Ainsi pour tout réel $x$ de l'intervalle $[-8~;~8]$ : \[f(x) = 5 - 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right).\]
2. En tenant compte du fait que l'on doit laisser une hauteur de sécurité de 50 cm, quelle doit être la hauteur maximale exprimée en mètre d'un véhicule motorisé pour qu'il puisse passer sous le pont ? On arrondira le résultat à $10^{-1}$.
Avec le graphique, on voit que les véhicules motorisés évoluent dans l'intervalle $[-4;4]$, graphiquement, on voit que la hauteur minimale sur $[-4;4]$ est réalisée en $x=4$ et vaut $f(4)= 5-0,5\left(\text{e}^{0,2\times 4} + \text{e}^{-0,2\times 4}\right)= 5 -0,5\left(\text{e}^{0,8} + \text{e}^{-0,8}\right)\approx 3,66$$ Comme $3,66-0,5=3,16 $
La hauteur maximale exprimée en mètre d'un véhicule motorisé pour qu'il puisse passer sous le pont est de 3,10m$
3. Montrer que la fonction $f'$ dérivée de la fonction $f$ est définie, pour tout réel $x$ de l'intervalle $[-8~;~8]$, par $f'(x) = 0,1\text{e}^{-0,2x}\left(1 - \text{e}^{0,4x}\right)$.
$$\begin{array}{rl} f(x) & = 5 - 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\\ f'(x)& = - 0,5\left(0,2\text{e}^{0,2x} -0,2 \text{e}^{-0,2x}\right)\\ & = -0,5\times 0,2 \text{e}^{0,2x} + 0,5\times 0,2 \text{e}^{-0,2x}\\ & = -0,1 \text{e}^{0,2x} + 0,1 \text{e}^{-0,2x}\\ & = 0,1 \text{e}^{-0,2x} \left(1 - \dfrac{\text{e}^{0,2x}}{\text{e}^{-0,2x} }\right)\\ & = 0,1 \text{e}^{-0,2x} \left(1 - \text{e}^{0,4x} \right)\\ \end{array}$$
4. Étudier le signe de $f'(x)$ sur $[-8~;~8]$. En déduire le tableau de variation de $f$ sur $[-8~;~8]$.
La fonction exponentielle étant strictement positive sur $\mathbb R$, on déduit que $f'(x)$ a le signe de $1 - \text{e}^{0,4x}$. $$\begin{array}{rl} f'(x) =0& \iff 1 - \text{e}^{0,4x} =0\\ & \iff \text{e}^{0,4x} =1\\ & \iff \ln\left ( \text{e}^{0,4x}\right ) =\ln 1\\ & \iff 0,4x =0\\ &\iff x=0\\ \end{array}$$ $$\begin{array}{rl} f'(x) >0& \iff 1 - \text{e}^{0,4x} >0\\ & \iff -\text{e}^{0,4x} > -1\\ & \iff \text{e}^{0,4x} < 1\\ & \iff \ln\left ( \text{e}^{0,4x}\right ) < \ln 1\\ & \iff 0,4x < 0\\ &\iff x < 0\\ \end{array}$$ Tableau de variation :
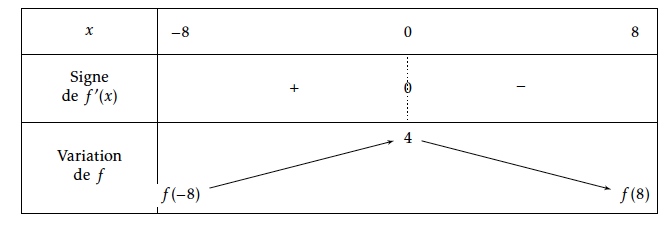$$f(-8)=f(8)=5- 0,5\left(\text{e}^{1,6} + \text{e}^{-1,6}\right)\approx 2,42$$

B-- Calculs d'aires

La façade du pont est la partie grisée représentée sur la figure précédente.

1. Calculer la valeur exacte de l'intégrale $I = \displaystyle\int_{-8}^8 \left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\:\text{d}x$.
$$\begin{array}{rl} \displaystyle\int_{-8}^8 \left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\:\text{d}x =\left [ \dfrac{\text{e}^{0,2x}}{0,2}+ \dfrac{\text{e}^{-0,2x}}{-0,2}\right ]_{-8}^{8}\\ & =\left [ 5\text{e}^{0,2x}-5\text{e}^{-0,2x} \right ]_{-8}^{8}\\ & =\left [ 5\left (\text{e}^{0,2x}- \text{e}^{-0,2x} \right)\right ]_{-8}^{8}\\ & 5\text{e}^{1,6}-5\text{e}^{-1,6}-\left (5\text{e}^{-1,6}-5\text{e}^{1,6}\right )\\ &=10\left (\text{e}^{1,6}- \text{e}^{-1,6}\right )\\ & \approx 47,51\\ \end{array}$$
$I = \displaystyle\int_{-8}^8 \left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\:\text{d}x =10\left (\text{e}^{1,6}- \text{e}^{-1,6}\right ) $
2. Vérifier que l'aire de la façade exprimée en m$^2$ vaut $5\left(\text{e}^{1,6} - \text{e}^{- 1,6}\right)$.
L'aire d'une façade est laire du domaine délimité par la droite d'équation $y=5$, la courbe $\mathcal{C}_f$ et les droites d'équation $x=-8$ et $x=8$. $$\begin{array}{rl} A &= \displaystyle\int_{-8}^8 \left(5-f(x)\right)\:\text{d}x\\ 5-f(x)&= 5-\left (5 - 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\right )\\ & = 0,5\left(\text{e}^{0,2x} + \text{e}^{-0,2x}\right)\\ A & =0,5 I\\ & \\ &=5\left (\text{e}^{1,6}- \text{e}^{-1,6}\right )\\ \end{array}$$
3. On veut peindre les deux façades du pont. En déduire l'aire $S$ exprimée en m$^2$ de la surface totale à peindre ; en donner une valeur en m$^2$ approchée à $10^{-2}$ près.
L'aire des deux façades vaut donc $$S= 2A =I=10\left (\text{e}^{1,6}- \text{e}^{-1,6}\right )u.a.\approx 47,51 m^2$$
4. La peinture utilisée pour peindre les façades du pont est vendue par bidon de 5 litres. Sachant que cette peinture a une propriété de recouvrement de 3 m$^2$ par litre, combien de bidons sont nécessaires pour recouvrir les deux faces de cette construction ?
Il faut donc environ $\dfrac{47,51}{3}\approx 15,84 L$ de peinture.
et donc comme $\dfrac{15,84}{3}\approx 3,2 L$
4 pots de peinture de 5 litres seront nécessaires pour peindre les deux façades de ce pont.