Baccalauréat STI2D–STL spécialité SPCL Polynésie - 11 juin 2015 - Correction Exercice 1

Page 2 sur 8: Correction Exercice 1

Correction de l'exercice 1 (4 points)

QCM

Cet exercice est un Q. C. M. Pour chacune des questions posées, une seule des quatre réponses est exacte. Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse choisie.
Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Dans cet exercice, on note $\mathbb R$ l'ensemble des nombres réels.
Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.

1. Le plan est rapporté à un repère orthonormé (O, A, B). L'ensemble $E$ des images des nombres complexes $z$ vérifiant la relation $|z| = 1$ est représenté en gras par :
   
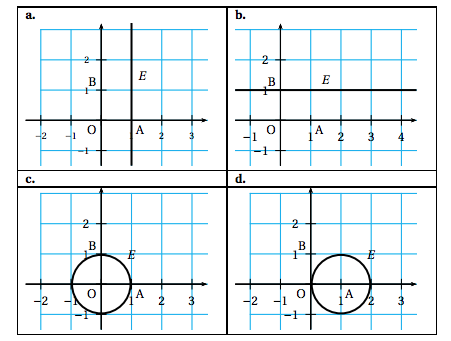$|z| = 1 \iff OM = 1$
L'ensemble $E$ est donc le cercle de centre $O$ de rayon 1.
Bonne réponse c.
2. Considérons les deux nombres complexes $$z_1 = \sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}\quad \text{et} \quad z_2 = - \sqrt{3} + \text{i}$$ où i est le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$. Le produit $z_1 \times z_2$ est égal à :
   
   1. $2\sqrt{2}\text{e}^{\text{i}\frac{11\pi}{12}}$
   2. $\left(1 + \sqrt{3}\right)(- 1 + \text{i})$
   3. $2\sqrt{2}\text{e}^{\text{i}\frac{13\pi}{12}}$
   4. $1 - \sqrt{3} + 2\text{i}$
L'écriture exponentielle d'un nombre complexe est $\rho e^{i\theta}$ où $\rho$ est son module et $\theta$ son argument.
• Module : $|z_2|=\sqrt{a^2+b^2}=\sqrt{\sqrt 3^2+1^2}=\sqrt{4}=2$
• Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= -\dfrac{\sqrt 3}{2 }\\ \sin(\theta)=\dfrac{b}{r} = \dfrac{1}{ 2} \end{array} \right.$$
Ainsi $\theta= \dfrac{5\pi}{6}$ convient; on a donc: $$z_2=\left[2 ; \dfrac{5\pi}{6}\right] \text{ ou } z_2=2 \left [\cos\left ( \dfrac{5\pi}{6}\right )+\text{i}\sin\left ( \dfrac{5\pi}{6}\right )\right ]= 2e^{ \text{i}\frac{ 5\pi}{6}}$$ On a alors $$\begin{array}{rl}z_1 \times z_2&=\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}} \times 2e^{ \text{i}\frac{ 5\pi}{6}} \\ &= 2\sqrt 2 \text{e}^{\text{i}\left(\frac{\pi}{4}+\frac{ 5\pi}{6}\right) }\\ &= 2\sqrt 2 \text{e}^{\text{i}\left(\frac{3\pi}{12}+\frac{ 10\pi}{12}\right) }\\ &= 2\sqrt 2 \text{e}^{\text{i}\left(\frac{13\pi}{12} \right) }\\ \end{array}$$
Bonne réponse c.
Bonne réponse c.
3. Voici la représentation graphique d'une fonction $f$. Cette courbe admet les quatre asymptotes suivantes :
   • deux asymptotes horizontales d'équations respectives $y = -1$ et $y = 0$ ;
   • deux asymptotes verticales d'équations respectives $x = 0$ et $x = 2$.
   
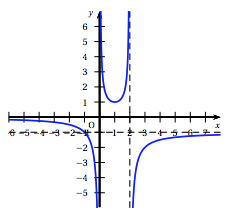
   Choisissez la bonne égalité :
   
   1. $\displaystyle\lim_{x \to + \infty} f(x) = 0$
   2. $\displaystyle\lim_{x \to 0^{-}} f(x) = - \infty$
   3. $\displaystyle\lim_{x \to 2^{+}} f(x) = + \infty$
   4. $\displaystyle\lim_{x \to - \infty} f(x) = - 1$
Bonne réponse b.
4. On considère l'équation différentielle $y' + 2y = 5$, où $y$ désigne une fonction de la variable réelle $x$ dérivable sur $\mathbb R$ et de dérivée notée $y'$. Une solution de cette équation est :
   
   1. $x \longmapsto \dfrac{5 - \text{e}^{- 2x}}{2}$
   2. $x \longmapsto \text{e}^{- 2x} - 5$
   3. $x \longmapsto \dfrac{\text{e}^{2x} - 5}{2}$
   4. $x \longmapsto \text{e}^{2x} + 2,5$
$y' + 2y = 5$ s'écrit $y'=-2y+5$; elle est donc du type $y'=ay+b$ où $a=-2$ et $b=5$;
la solution générale est $y=-\dfrac{b}{a}+ C \text{e}^{ax}$ où $C$ désigne une constante réelle quelconque.
Ici la solution générale de $y'=-2y+5$ est $y= \dfrac{5}{2}+ C \text{e}^{-2x}$ où $C$ désigne une constante réelle quelconque. $x \longmapsto \dfrac{5 - \text{e}^{- 2x}}{2}= \dfrac{5}{2}-\dfrac{1}{2} \text{e}^{-2x}$
Bonne réponse a.
Page suivante
Exercice 2
Page
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• Toutes les pages