Baccalauréat STI 2D/STL spécialité SPCL Métropole--La Réunion 7 septembre 2015
Exercice 1 4 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
- On considère le nombre complexe $z = 3\text{e}^{\text{i}\frac{\pi}{3}}$. Le nombre complexe conjugué de $z$ est égal à :
- a.$\overline{z} = - 3\text{e}^{\text{i}\frac{\pi}{3}}$
- b. $\overline{z} =3\text{e}^{-\text{i}\frac{\pi}{3}}$
- c. $\overline{z} = - 3\text{e}^{-\text{i}\frac{\pi}{3}}$
- d.$\overline{z} = 3\text{e}^{-\text{i}\frac{2\pi}{3}}$
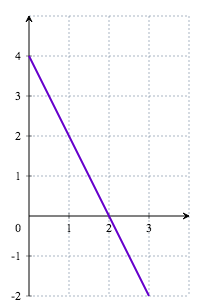
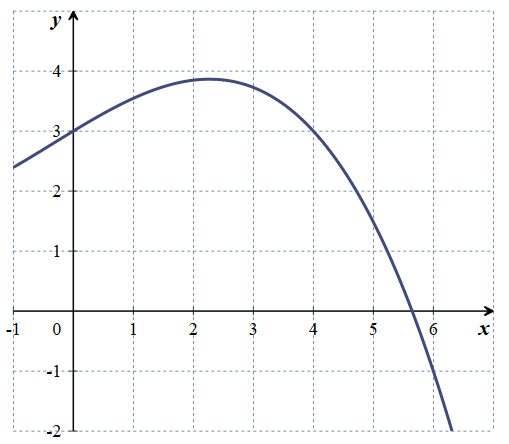
- La figure ci-dessous donne la courbe représentative d'une fonction! définie sur $\mathbb R$. En notant $I$ l'intégrale $\displaystyle\int_0^3 f(x)\:\text{d}x$, on a alors, en unités d'aire :
- a. $1< I < 3$
- b. $0 < I < 9$
- c. $9 < I < 12$
- d. $12 < I < 22$
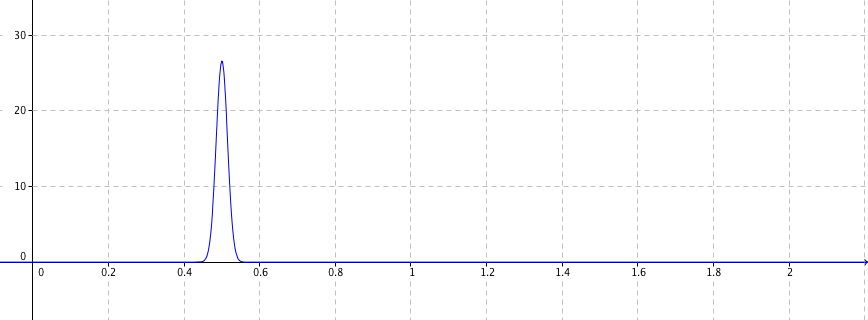
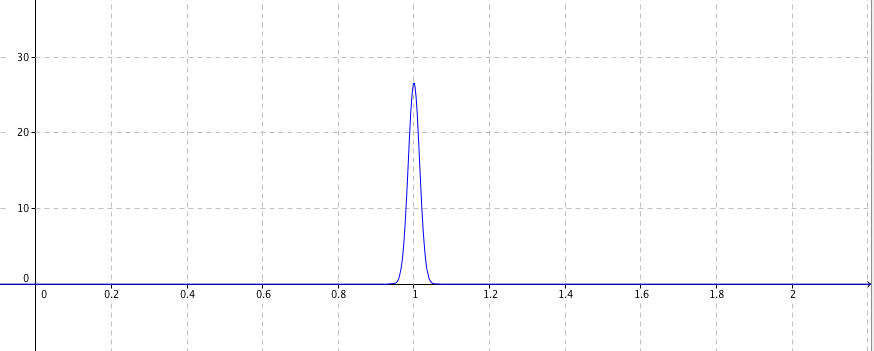
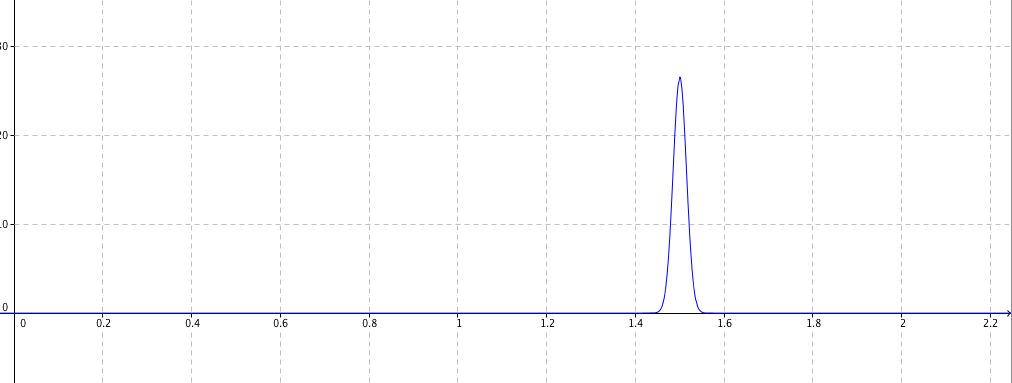
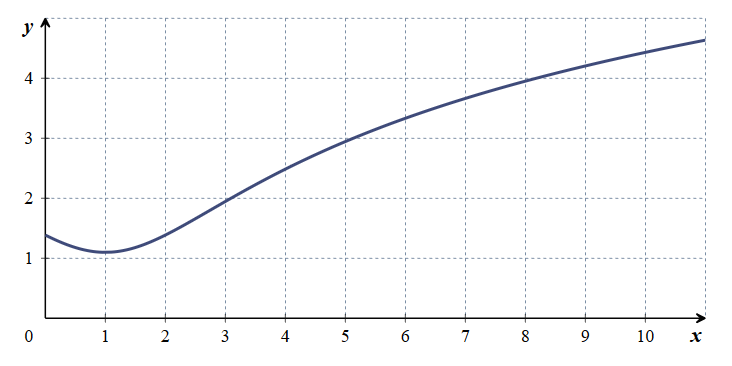
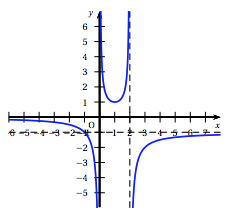
- La figure ci-dessous donne la courbe représentative de la fonction $g$ définie sur $[0~;~ +\infty[$ par \[g(x) = \ln \left(x^2 - 2x + 4\right).\]
- La courbe de la fonction dérivée de la fonction $g$ est :
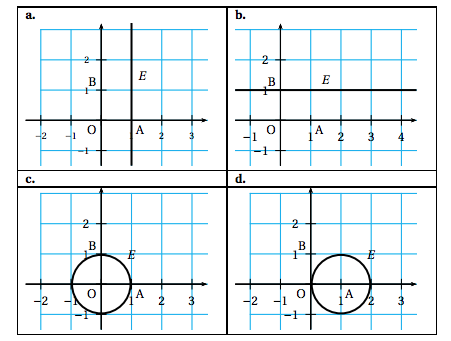
- a.
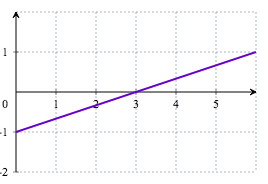
- b.
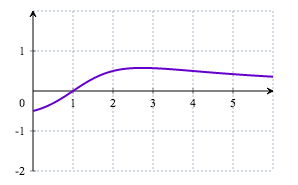
- c.
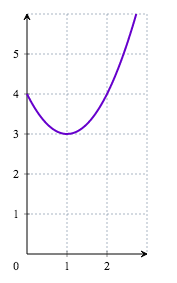
- d.
- a.
- La variable $X$ suit la loi normale d'espérance $3$ et d'écart type $6$. La probabilité $P(X < 3)$ vaut :
- a. $0,5$
- b.$0,997$
- c.$3$
- d.$0$
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse.
- On considère le nombre complexe $z = 3\text{e}^{\text{i}\frac{\pi}{3}}$. Le nombre complexe conjugué de $z$ est égal à :
- La bonne réponse est b. $\overline{z} =3\text{e}^{-\text{i}\frac{\pi}{3}}$
Le conjugugué de $z=re^{i\theta}$ est $re^{-i\theta}$
- La figure ci-dessous donne la courbe représentative d'une fonction! définie sur $\mathbb R$. En notant $I$ l'intégrale $\displaystyle\int_0^3 f(x)\:\text{d}x$, on a alors, en unités d'aire :
- a. $1< I < 3$
- b. $0 < I < 9$
- c. $9 < I < 12$
- d. $12 < I < 22$
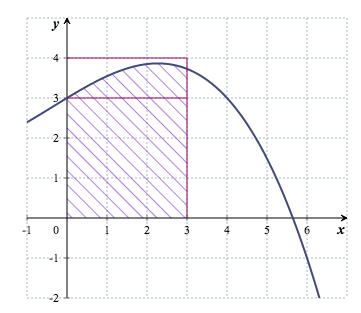
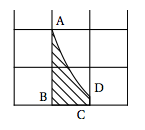
- La courbe représentative de la fonction $f$ est située au dessus de l'axe des abscisses, donc l'intégrale $\displaystyle\int_0^3 f(x)dx $ est égale à l'aire, exprimée en unités d'aire, du domaine hachuré compris entre la courbe, l'axe des abscisses, l'axe des ordonnées et la droite d'équation $x=3$. Or cette aire peut être encadrée par l'aire d'un carré de côté 3 et l'aire d'un rectangle de longueur 4 et de largeur 3. D'où $$3^2<\displaystyle\int_0^3 f(x)dx <3\times 4 $$ $$9<\displaystyle\int_0^3 f(x)dx <12$$
- La figure ci-dessous donne la courbe représentative de la fonction $g$ définie sur $[0~;~ +\infty[$ par $$g(x) = \ln \left(x^2 - 2x + 4\right).$$
- La courbe de la fonction dérivée de la fonction $g$ est :
- a.

- b.

- c.

- d.

Par lecture graphique : Sur l'intervalle $[0;1]$ la fonction $g$ est décroissante - a.
- La variable $X$ suit la loi normale d'espérance $3$ et d'écart type $6$. La probabilité $P(X < 3)$ vaut :
- a. $0,5$
- b.$0,997$
- c.$3$
- d.$0$
La variable $X$ suit la loi normale d'espérance 3 alors, $P(X < 3)= 0,5$
donc pour tout réel $x$ de l'intervalle $[0;1], g’(x)\leq 0$.
Sur l'intervalle $[0;+\infty[$ la fonction $g$ est croissante donc pour tout réel $x\geq 1, g’(x)\geq 0$.
La courbe 2 est la seule des quatre courbes qui peut convenir.
Exercice 2 6 points
Dans cet exercice, tous les résultats seront arrondis à $10^{-2}$ près.
Un smartphone est équipé d'une batterie Li-ion qui débite en usage normal un courant d'intensité moyenne $I$ de 0,03 ampère (A). La capacité $C$ de cette batterie, exprimée en ampères-heures (Ah), est la quantité maximale d'électricité qu'elle peut emmagasiner. On dit que la batterie a effectué un cycle de charge lorsque la quantité d'électricité absorbée, éventuellement en plusieurs fois, est égale à sa capacité. Lors des 300 premiers cycles de charge de la batterie, sa capacité reste égale à 1,8 Ah.
- L'autonomie $T$ de ce smartphone, en heures, est fonction de la capacité $C$ de sa batterie et de l'intensité moyenne $I$ du courant qu'elle débite en usage normal. On estime que $T = 0,7 \times \dfrac{C}{I}$. Calculer l'autonomie $T$, en heures, de ce smartphone au cours de l'un des $300$ premiers cycles de charge.
- On considère qu'après $300$ cycles de charge, l'autonomie de la batterie diminue de 1 % à chaque nouveau cycle de charge. Pour tout entier naturel $n$, on note $T_n$ l'autonomie, en heures, de la batterie au bout de " $300 + n$ " cycles de charge. On admet que $T_0 = 42$.
- Calculer $T_1$ et $T_2$. Interpréter les résultats.
- Exprimer $T_{n+1}$ en fonction de $T_n$ ;
- Justifier que $T_n = 42 \times 0,99^n$.
- Un utilisateur souhaite déterminer à partir de combien de cycles de charge l'autonomie de la batterie aura diminué de moitié par rapport à son état initial.
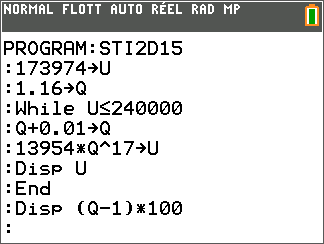
- On propose l'algorithme suivant pour déterminer le nombre de cycles de charge correspondant. $$\begin{array}{|c|}\hline \text{Variables}\\ \hspace{0.4cm}n : \text{nombre entier naturel}\\ \hspace{0.4cm}T : \text{nombre réel}\\ \hspace{0.4cm}q : \text{nombre réel}\\ \text{Initialisation}\\ \hspace{0.4cm}n \text{prend la valeur }a\\ \hspace{0.4cm}T \text{prend la valeur } 42\\ \hspace{0.4cm}q \text{ prend la valeur } 0,99\\ \text{Traitement}\\ \hspace{0.4cm}\text{Tant que } \ldots \ldots\\ \hspace{0.7cm}T \text{ prend la valeur } \ldots \ldots\\ \hspace{0.7cm}n\text{ prend la valeur } \ldots \ldots\\ \hspace{0.4cm}\text{Fin Tant que }\\ \text{Sortie}\\ \hspace{0.4cm}\text{Afficher } n + 300\\ \hline \end{array}$$ Recopier et compléter la partie relative au traitement.
- Déterminer à partir de combien de cycles de charge l'autonomie de la batterie aura diminué de moitié par rapport à son état initial.
- Lorsque l'autonomie de la batterie devient inférieure à $5$ heures, on estime qu'elle ne permet plus un usage normal du smartphone. Le nombre de cycles de charge correspondant est alors appelé durée de vie de la batterie. Déterminer la durée de vie de cette batterie.
Correction de l'exercice 2 (5 points)
Dans cet exercice, tous les résultats seront arrondis à $10^{-2}$ près.
Un smartphone est équipé d'une batterie Li-ion qui débite en usage normal un courant d'intensité moyenne $I$ de 0,03 ampère (A). La capacité $C$ de cette batterie, exprimée en ampères-heures (Ah), est la quantité maximale d'électricité qu'elle peut emmagasiner. On dit que la batterie a effectué un cycle de charge lorsque la quantité d'électricité absorbée, éventuellement en plusieurs fois, est égale à sa capacité. Lors des 300 premiers cycles de charge de la batterie, sa capacité reste égale à 1,8 Ah.
- L'autonomie $T$ de ce smartphone, en heures, est fonction de la capacité $C$ de sa batterie et de l'intensité moyenne $I$ du courant qu'elle débite en usage normal. On estime que $T = 0,7 \times \dfrac{C}{I}$. Calculer l'autonomie $T$, en heures, de ce smartphone au cours de l'un des $300$ premiers cycles de charge. $$T=0,7\times \dfrac{1,8}{0,03}=42$$ Au cours de l'un des 300 premiers cycles de charge l'autonomie de ce smartphone est de 42 heures.
- On considère qu'après $300$ cycles de charge, l'autonomie de la batterie diminue de 1 % à chaque nouveau cycle de charge. Pour tout entier naturel $n$, on note $T_n$ l'autonomie, en heures, de la batterie au bout de " $300 + n$ " cycles de charge. On admet que $T_0 = 42$.
- Calculer $T_1$ et $T_2$. Interpréter les résultats. Le coefficient multiplicateur associé à une baisse de 1 % est $1-\dfrac{1}{100}=0,99$. D'où : $T_1=T_0\times 0,99 $ soit $T_1=42\times 0,99=41,58 $ et $T_2=T_1×0,99 $ soit $ T_2=41,58\times 0,99=41,1642$
- $T_1=41,58$ et $T_2\approx 41,16$. L'autonomie de la batterie au bout de 301 et 302 cycles de charge est respectivement de 41,58 heures et 41,16 heures.
- Exprimer $T_{n+1}$ en fonction de $T_n$ ; $T_{n+1}=0,99 T_n$
- Justifier que $T_n = 42 \times 0,99^n$. $(T_n)$ est une suite géométrique de raison $q=0,99$ et de premier terme $T_0=42$ alors, pour tout entier $n, T_n=42\times 0,99^n.$
- On propose l'algorithme suivant pour déterminer le nombre de cycles de charge correspondant. $$\begin{array}{|c|}\hline \text{Variables}\\ \hspace{0.4cm}n : \text{nombre entier naturel}\\ \hspace{0.4cm}T : \text{nombre réel}\\ \hspace{0.4cm}q : \text{nombre réel}\\ \text{Initialisation}\\ \hspace{0.4cm}n \text{prend la valeur }a\\ \hspace{0.4cm}T \text{prend la valeur } 42\\ \hspace{0.4cm}q \text{ prend la valeur } 0,99\\ \text{Traitement}\\ \hspace{0.4cm}\text{Tant que } \ldots \ldots\\ \hspace{0.7cm}T \text{ prend la valeur } \ldots \ldots\\ \hspace{0.7cm}n\text{ prend la valeur } \ldots \ldots\\ \hspace{0.4cm}\text{Fin Tant que }\\ \text{Sortie}\\ \hspace{0.4cm}\text{Afficher } n + 300\\ \hline \end{array}$$ Recopier et compléter la partie relative au traitement. $$\begin{array}{|c|}\hline \text{Variables}\\ \hspace{0.4cm}n : \text{nombre entier naturel}\\ \hspace{0.4cm}T : \text{nombre réel}\\ \hspace{0.4cm}q : \text{nombre réel}\\ \text{Initialisation}\\ \hspace{0.4cm}n \text{prend la valeur }a\\ \hspace{0.4cm}T \text{prend la valeur } 42\\ \hspace{0.4cm}q \text{ prend la valeur } 0,99\\ \text{Traitement}\\ \hspace{0.4cm}\text{Tant que } T> 21\\ \hspace{0.7cm}T \text{ prend la valeur }T\times q\\ \hspace{0.7cm}n\text{ prend la valeur } n+1\\ \hspace{0.4cm}\text{Fin Tant que }\\ \text{Sortie}\\ \hspace{0.4cm}\text{Afficher } n + 300\\ \hline \end{array}$$
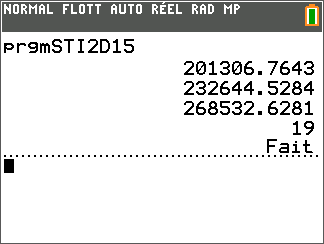
- Déterminer à partir de combien de cycles de charge l'autonomie de la batterie aura diminué de moitié par rapport à son état initial. méthode 1 On programme l'algorithme sur la calculatrice : L'autonomie de la batterie aura diminué de moitié par rapport à son état initial au bout de 369 cycles de charge.
- Lorsque l'autonomie de la batterie devient inférieure à 5 heures, on estime qu'elle ne permet plus un usage normal du smartphone. Le nombre de cycles de charge correspondant est alors appelé durée de vie de la batterie. Déterminer la durée de vie de cette batterie. $$\begin{array}{rl} 42 \times 0,99^n \leq 5&\iff 0,99^n \leq \dfrac{5}{42}\\ & \iff \ln\left( 0,99^n \right )\leq \ln\left(\dfrac{5}{42}\right) \\ &\iff n\ln\left( 0,99 \right )\leq \ln\left(\dfrac{5}{42}\right) \\ &\iff n\geq \dfrac{\ln\left(\dfrac{5}{42}\right)}{\ln\left( 0,99 \right )} \text{ car } \ln\left( 0,99 \right ) < 0 \\ \end{array}$$ Or $$ \dfrac{\ln\left(\dfrac{5}{42}\right)}{\ln\left( 0,99 \right )} \approx 212 $$ alors le nombre de cycles est 369. La durée de vie de cette batterie est de 512 cycles de charge.
- si la concentration est supérieure à 30 ppm pendant au moins 120 minutes ;
- si la concentration est supérieure à 50 ppm pendant au moins 60 minutes ;
- si la concentration est supérieure à 100 ppm pendant au moins la minutes ;
- si la concentration est supérieure à 300 ppm pendant au moins 3 minutes.
- Estimer au bout de combien de temps devrait retentir un signal d'alarme.
- Une personne présente dans la pièce depuis le début d'un tel accident risquerait-elle de présenter des symptômes? Si oui, lesquels?
- Calculer la concentration de monoxyde de carbone en ppm dans la pièce:
- au moment de l'accident;
- 30 minutes après.
- À l'aide du graphique de la partie A, conjecturer les variations de la concentration de monoxyde de carbone dans la pièce en fonction du temps.
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0~;~8]$.
- Montrer que pour tout réel $t$ de l'intervalle $[0~;~8]$, $f'(t) = 200(1 - t)\text{e}^{-t}$.
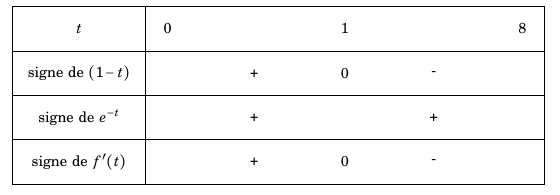
- Étudier le signe de $f'(t)$ sur l'intervalle $[0~;~8]$.
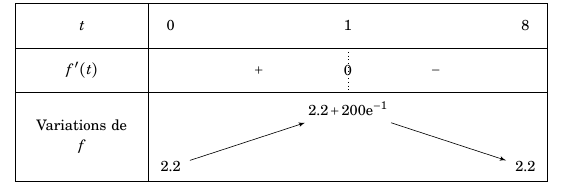
- Valider ou invalider la conjecture émise à la question 2.
- On note $F$ la fonction définie sur l'intervalle $[0~;~8]$ par \[F(t) = 2,2 t - 200(t + 1)\text{e}^{-t}.\] On admet que $F$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~8]$.
- On rappelle que la valeur moyenne d'une fonction continue sur un intervalle $[a~;b]$ est le nombre réel défini par : $\dfrac{1}{b-a} \displaystyle\int_a^b f(t)\:\text{d}t$. Calculer la valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident.
- Pour des raisons de sécurité, le ministère du travail fixe un seuil pour la concentration moyenne de monoxyde de carbone. Ce seuil est de $50$~ppm pour une période de 8 heures. La sécurité des personnes présentes dans la pièce aurait-elle été remise en cause lors de l'accident simulé ?
- si la concentration est supérieure à 30 ppm pendant au moins 120 minutes ;
- si la concentration est supérieure à 50 ppm pendant au moins 60 minutes ;
- si la concentration est supérieure à 100 ppm pendant au moins la minutes ;
- si la concentration est supérieure à 300 ppm pendant au moins 3 minutes.
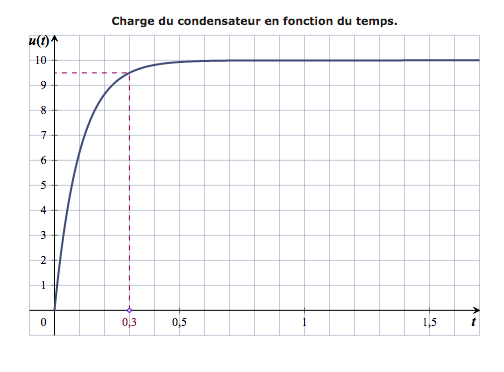
- Estimer au bout de combien de temps devrait retentir un signal d'alarme. Par lecture graphique, on constate que la condition «la concentration est supérieure à 50 ppm pendant au moins 60 minutes» est la premiére a être réalisée d'où :
- Une personne présente dans la pièce depuis le début d'un tel accident risquerait-elle de présenter des symptômes? Si oui, lesquels? La concentration de monoxyde de carbone dépasse 20 ppm et est inférieure à 80 ppm d'après le document 2 :
- Calculer la concentration de monoxyde de carbone en ppm dans la pièce:
- au moment de l'accident; $f(0)=2,2$ par conséquent, au moment de l'accident, la concentration de monoxyde de carbone en ppm dans la pièce est de 2,2 ppm.
- 30 minutes après. $$f(0,5)=2,2+200\times0,5\times \text{e}^{-0,5}=2,2+100\times \text{e}^{-0,5}\approx 62,85$$ Une demi-heure après le début de l'accident, la concentration de monoxyde de carbone en ppm dans la pièce est de 62,85 ppm.
- À l'aide du graphique de la partie A, conjecturer les variations de la concentration de monoxyde de carbone dans la pièce en fonction du temps. Par lecture graphique,on obtient :
- On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0~;~8]$.
- Montrer que pour tout réel $t$ de l'intervalle $[0~;~8]$, $f'(t) = 200(1 - t)\text{e}^{-t}$. $f$ est dérivable comme somme de deux fonctions dérivables. $f=u v + 2,2$ d'où $f'=u'v+v'u $ avec pour tout réel $t$, dans $[0; 8]$ : $\left\{ \begin{array}{l} u(t)~ =200 t\\ v(t)~ =\text{e}^{-t} \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(t)~ =200 \\ v'(t)~ =-\text{e}^{-t} \end{array}\right.$ $$ \begin{array}{cl} f'(t)&=200\text{e}^{-t}+ \left (-\text{e}^{-t}\right )\times 200 t \\ & =200\text{e}^{-t}(1-t) \\ &=200(1 - t)\text{e}^{-t} \end{array} $$
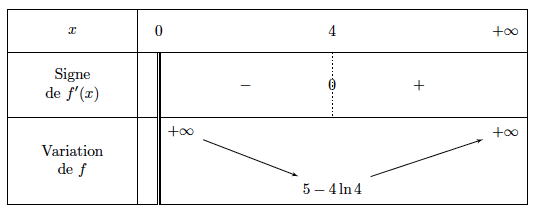
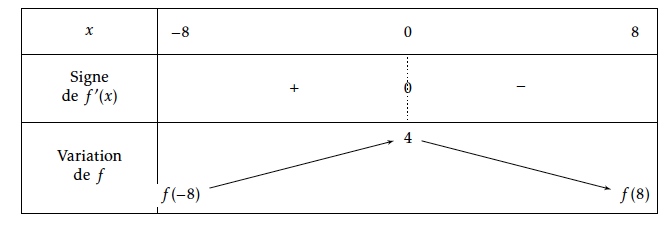
- Étudier le signe de $f'(t)$ sur l'intervalle $[0~;~8]$. Comme pour tout réel $t, e^{-t}>0$ alors, $f′(t)$ est du même signe que $1-t$ sur l'intervalle $[0;8]$. Or $$1-t\geq 0 0\iff -t\geq -1\iff t \leq 1$$ D'où le tableau du signe de $f′(t)$:
- Valider ou invalider la conjecture émise à la question 2. Les variations de la fonction $f$ se déduisent du signe de sa dérivée. D'où le tableau de variation de la fonction :
- On note $F$ la fonction définie sur l'intervalle $[0~;~8]$ par \[F(t) = 2,2 t - 200(t + 1)\text{e}^{-t}.\] On admet que $F$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~8]$.
- On rappelle que la valeur moyenne d'une fonction continue sur un intervalle $[a~;b]$ est le nombre réel défini par : $\dfrac{1}{b-a} \displaystyle\int_a^b f(t)\:\text{d}t$. Calculer la valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident. $$\begin{array}{rl} \dfrac{1}{8-0}\displaystyle\int_0^8f(t)\;\text{d}t & = \dfrac{1}{8-0}\left [F(8)-F(0)\right] \\ & \dfrac{1}{8-0}\left [(2,2\times 8-200\times 9\times e^{-8})-(2,2\times 0-200\times 9\times e^{0})\right] \\ &\dfrac{1}{8-0}\left [(17,6-1800\times e^{-8})+1800\right]\\ &= 27,2-225\times e^{-8} \\ &\approx 27,12 \end{array}$$
- Pour des raisons de sécurité, le ministère du travail fixe un seuil pour la concentration moyenne de monoxyde de carbone. Ce seuil est de $50$~ppm pour une période de 8 heures. La sécurité des personnes présentes dans la pièce aurait-elle été remise en cause lors de l'accident simulé ?
La valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident est d'environ 27,12 ppm.La valeur moyenne de la concentration de monoxyde de carbone lors des 8 heures qui ont suivi l'accident est inférieure à 50 ppm par conséquent, la sécurité des personnes présentes dans la pièce n'a pas été remise en cause lors de l'accident simulé. - $\lambda$ est un nombre réel strictement positif. Une variable aléatoire suit la loi exponentielle de paramètre $\lambda$ si sa densité de probabilité est définie sur $[0~;~+\infty[$ par $f(x) = \lambda\text{e}^{-\lambda x}$.
- L'espérance d'une variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda$ est $E(X) = \dfrac{1}{\lambda}$.
-
- Pour illustrer la situation un élève utilise un tableur. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline &A &B &C &D &E &F &G &H &I &J &K &L &M &N &O &P &Q &R &S &T\\ \hline 1 &\text{Année }&1769 &1800 &1808 &1857 &1865 &1868 &1906 &1925 &1927 &1933 &1952 &1957 &1971 &1989 &2004 &2008 &2010 &2014 & \text{Total}\\ \hline 2 & & &31 &8 &49 &8 &3 &38 &19 &2 &6 &19 &5 &14 &18 &15 &4 &2 &4 &245\\ \hline \end{array}\normalsize $$
Proposer un titre pour la cellule A2 grisée. - Quelle formule a saisi l'élève dans la cellule C2 afin de compléter ce tableau jusqu'à la colonne S par " recopie automatique vers la droite " ?
- Pour illustrer la situation un élève utilise un tableur. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline &A &B &C &D &E &F &G &H &I &J &K &L &M &N &O &P &Q &R &S &T\\ \hline 1 &\text{Année }&1769 &1800 &1808 &1857 &1865 &1868 &1906 &1925 &1927 &1933 &1952 &1957 &1971 &1989 &2004 &2008 &2010 &2014 & \text{Total}\\ \hline 2 & & &31 &8 &49 &8 &3 &38 &19 &2 &6 &19 &5 &14 &18 &15 &4 &2 &4 &245\\ \hline \end{array}\normalsize $$
-
- Calculer en années la moyenne m, arrondie à $10^{-2}$ près, du temps écoulé entre deux séismes majeurs le long de la faille de San Andreas en Californie.
- Justifier qu'une approximation du paramètre $\lambda$ de la loi exponentielle suivie par la variable aléatoire $X$ est 0,0694 .
-
- Calculer $P(X \leqslant 20)$ à $10^{-2}$ près.
- L'affirmation du sismologue paraît -elle cohérente avec cette modélisation par une loi exponentielle?
- Le dernier séisme majeur a eu lieu en 2014 à Napa. Calculer la probabilité qu'il n'y ait pas d'autres séismes majeurs le long de la faille de San Andreas, en Californie, avant 2050. On arrondira à $10^{-2}$ près.
-
- Résoudre l'équation $1 - \text{e}^{-0,0694t} = 0,95$.
- Interpréter ce résultat.
- $\lambda$ est un nombre réel strictement positif. Une variable aléatoire suit la loi exponentielle de paramètre $\lambda$ si sa densité de probabilité est définie sur $[0~;~+\infty[$ par $f(x) = \lambda\text{e}^{-\lambda x}$.
- L'espérance d'une variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda$ est $E(X) = \dfrac{1}{\lambda}$.
-
- Pour illustrer la situation un élève utilise un tableur. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline &A &B &C &D &E &F &G &H &I &J &K &L &M &N &O &P &Q &R &S &T\\ \hline 1 &\text{Année }&1769 &1800 &1808 &1857 &1865 &1868 &1906 &1925 &1927 &1933 &1952 &1957 &1971 &1989 &2004 &2008 &2010 &2014 & \text{Total}\\ \hline 2 & & &31 &8 &49 &8 &3 &38 &19 &2 &6 &19 &5 &14 &18 &15 &4 &2 &4 &245\\ \hline \end{array}\normalsize $$
Proposer un titre pour la cellule A2 grisée. Le titre suggéré pour la cellule A2 est « Temps écoulé entre deux seismes majeurs » - Quelle formule a saisi l'élève dans la cellule C2 afin de compléter ce tableau jusqu'à la colonne S par " recopie automatique vers la droite " ?
La formule saisie dans la cellule C2 est : « = C1 - B1 » - Pour illustrer la situation un élève utilise un tableur. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline &A &B &C &D &E &F &G &H &I &J &K &L &M &N &O &P &Q &R &S &T\\ \hline 1 &\text{Année }&1769 &1800 &1808 &1857 &1865 &1868 &1906 &1925 &1927 &1933 &1952 &1957 &1971 &1989 &2004 &2008 &2010 &2014 & \text{Total}\\ \hline 2 & & &31 &8 &49 &8 &3 &38 &19 &2 &6 &19 &5 &14 &18 &15 &4 &2 &4 &245\\ \hline \end{array}\normalsize $$
-
- Calculer en années la moyenne m, arrondie à $10^{-2}$ près, du temps écoulé entre deux séismes majeurs le long de la faille de San Andreas en Californie. Il y a 17 périodes de temps écoulé d'où $$m=\dfrac{245}{17}\approx 14,41$$ La moyenne du temps écoulé entre deux séismes majeurs le long de la faille de San Andreas est de 14,41 années.
- Justifier qu'une approximation du paramètre $\lambda$ de la loi exponentielle suivie par la variable aléatoire $X$ est 0,0694 .
L'espérance d'une variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda$ est $E(X)=\dfrac{1}{\lambda}$ d'où $$\dfrac{1}{\lambda}=14,41\iff\lambda= \dfrac{1}{14,41}\approx 0,0694$$ Une approximation du paramètre $\lambda$ de la loi exponentielle suivie par la variable aléatoire X est 0,0694.
-
- Calculer $P(X \leqslant 20)$ à $10^{-2}$ près.
- L'affirmation du sismologue paraît -elle cohérente avec cette modélisation par une loi exponentielle?
$$\begin{array}{rl} P(X\leq 20)&=\displaystyle\int_0^{20} 0,0694 e^{-0,0694 t } \;\text{d}t \\ &= \left [ -e^{-0,0694 t }\right ]_0^{20}\\ & = \left [F(20)-F(0)\right] \\ & -e^{-0,0694 \times 20 } -(-e^{0})\\ &=1- e^{-1,388}\\ &\approx 0,75 \end{array}$$ $$P(X\leq 20) \approx 0,75$$
$P(X\leq 20) \approx 0,75$ donc l'affirmation du sismologue est cohérente avec cette modélisation.
- Le dernier séisme majeur a eu lieu en 2014 à Napa. Calculer la probabilité qu'il n'y ait pas d'autres séismes majeurs le long de la faille de San Andreas, en Californie, avant 2050. On arrondira à $10^{-2}$ près.
-
- Résoudre l'équation $1 - \text{e}^{-0,0694t} = 0,95$. $$\begin{array}{rl} 1-e^{-0,0694 t } =0,95&\iff e^{-0,0694 t } = 0,05 \\ &\iff \ln \left (e^{-0,0694 t }\right )=\ln(0,05)\\ & \iff -0,0694 t= \ln(0,05)\\ & \iff t = -\dfrac{\ln(0,05)}{0,0694}\\ &t\approx 43,166 \text{ soit } 43,17 \text{ au centième près. } \end{array}$$ L'équation $1 - \text{e}^{-0,0694t} = 0,95$ admet pour solution $t = -\dfrac{\ln(0,05)}{0,0694}\approx 43,17$.
- Interpréter ce résultat. $$\begin{array}{rl} P(X\leq t)&=\displaystyle\int_0^{t} 0,0694 e^{-0,0694 x } \;\text{d}x \\ &= \left [ -e^{-0,0694 x }\right ]_0^{x}\\ & = \left [F(x)-F(0)\right] \\ & 1-e^{-0,0694 t } \\ \end{array}$$ on a donc :$1-e^{-0,0694 t } =0,95 $ si $t\approx 43,17$, donc $P(X\leq 43,17)=0,95 $: la probabilité qu'il y ait un séisme majeur dans les 44 prochaines années est supérieur à 95%.
Selon ce modèle, Le risque d'un séisme majeur le long de la faille de San Andreas dans les 44 prochaines années est supérieur à 95 %.
méthode 2 On cherche le plus petit entier n qu'il faut ajouter à 300, solution de l'inéquation : $$\begin{array}{rl} 42 \times 0,99^n \leq 42 \times 0,5&\iff 0,99^n \leq 0,5\\ & \iff \ln\left( 0,99^n \right )\leq \ln(0,5) \\ &\iff n\ln\left( 0,99 \right )\leq \ln(0,5) \\ &\iff n\geq \dfrac{\ln(0,5)}{\ln\left( 0,99 \right )} \text{ car } \ln\left( 0,99 \right ) < 0 \\ \end{array}$$ Or $$ \dfrac{\ln(0,5)}{\ln\left( 0,99 \right )} \approx 69 $$ alors le nombre de cycles est 369. L' autonomie de la batterie aura diminué de moitié par rapport à son état initial au bout de 369 cycles de charge.
Exercice 3 6 points
" Avec une centaine de décès en moyenne par an, le monoxyde de carbone (CO) est la première cause de mortalité accidentelle par intoxication en France. Pourtant certains symptômes annonciateurs d'une intoxication au monoxyde de carbone existent. Maux de tête, nausées et vomissements sont notamment les premiers signes qui doivent alerter. Bien identifiés, ils permettent de réagir rapidement et d'éviter le pire."
Source Ministère des Affaires Sociales et de la Santé. (octobre 2012)
Document 1
La société COalerte fabrique un modèle de détecteurs qui enregistre en temps réel la concentration de monoxyde de carbone en parties par million (ppm). Un tel détecteur produit un signal d'alarme respectant les modalités fixées par la norme européenne EN 50 291 ci-dessous. Il déclenche un signal d'alarme :
Document 2 
Un laboratoire d'essais procède à des tests sur un détecteur produit par la société COalerte en simulant un accident qui provoque une concentration anormale de monoxyde de carbone dans une pièce.
Partie A
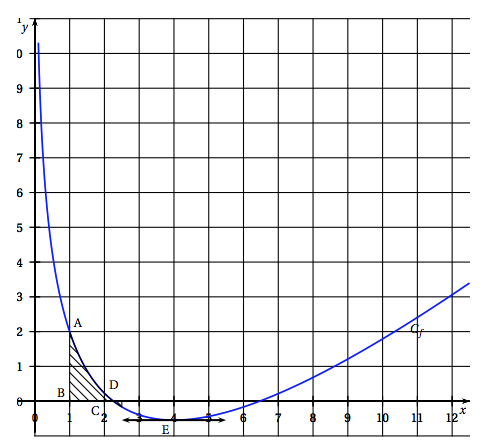
Le laboratoire relève la concentration de monoxyde de carbone en fonction du temps, exprimé en heures. Les enregistrements effectués sur une période de 8 heures se traduisent par la représentation graphique ci-dessous.
Partie B
Dans cette partie, tous les résultats seront arrondis à $10^{-2}$ près.
La concentration de monoxyde de carbone exprimée en ppm dans la pièce en fonction du temps, exprimé en heures, est modélisée par la fonction $f$ définie sur $[0~;~8]$ par \[f(t) = 2,2 + 200t\text{e}^{-t}.\]
Correction de l'exercice 3 (5 points)
" Avec une centaine de décès en moyenne par an, le monoxyde de carbone (CO) est la première cause de mortalité accidentelle par intoxication en France. Pourtant certains symptômes annonciateurs d'une intoxication au monoxyde de carbone existent. Maux de tête, nausées et vomissements sont notamment les premiers signes qui doivent alerter. Bien identifiés, ils permettent de réagir rapidement et d'éviter le pire."
Source Ministère des Affaires Sociales et de la Santé. (octobre 2012)
Document 1
La société COalerte fabrique un modèle de détecteurs qui enregistre en temps réel la concentration de monoxyde de carbone en parties par million (ppm). Un tel détecteur produit un signal d'alarme respectant les modalités fixées par la norme européenne EN 50 291 ci-dessous. Il déclenche un signal d'alarme :
Document 2 
Un laboratoire d'essais procède à des tests sur un détecteur produit par la société COalerte en simulant un accident qui provoque une concentration anormale de monoxyde de carbone dans une pièce.
Partie A
Le laboratoire relève la concentration de monoxyde de carbone en fonction du temps, exprimé en heures. Les enregistrements effectués sur une période de 8 heures se traduisent par la représentation graphique ci-dessous.
avec la précision permise par le graphique, un signal d'alarme devrait retentir au bout de 80 minutes.
Une personne présente dans la pièce depuis le début d'un tel accident risque de présenter les symptômes suivants : «Troubles du rythme cardiaque ressentis chez les personnes les plus sensibles, souffrant de coronaropathie» et «Céphalées et nausées chez les enfants».
Partie B
Dans cette partie, tous les résultats seront arrondis à $10^{-2}$ près.
La concentration de monoxyde de carbone exprimée en ppm dans la pièce en fonction du temps, exprimé en heures, est modélisée par la fonction $f$ définie sur $[0~;~8]$ par \[f(t) = 2,2 + 200t\text{e}^{-t}.\]
$f$ est croissante sur $[0;1]$.
$f$ est décroissante sur $[1;8]$.
Exercice 4 4 points
Un sismologue déclare en janvier 2014 : "Le risque d'un séisme majeur le long de la faille de San Andreas, en Californie, dans les vingt prochaines années est supérieur à 70 % ".
On s'intéresse au temps, exprimé en années, écoulé entre deux séismes majeurs le long de cette faille en Californie. On admet que ce temps est une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$.
Document 1
La faille de San Andreas, en Californie : séismes majeurs de magnitude supérieure ou égale à 5. $$\begin{array}{|c|c|c|}\hline \text{Ville} & \text{Année} &\text{Magnitude}\\ \hline\hline \text{Comté d'Orange} & 1769 & 6\\ \hline \text{San Diego } &1800 & 6,5\\ \hline \text{San Francisco }&1808 &6\\ \hline \text{Fort Tejon } &1857 &8,3\\ \hline \text{Monts Santa Cruz}&1865 &6,5\\ \hline \text{Hayward } &1868 &6,9\\ \hline \text{San Francisco } &1906 &8,2\\ \hline \text{Santa Barbara } &1925 &6,3\\ \hline \text{Santa Barbara } &1927 &7,3\\ \hline \text{Long Beach } &1933 &6,3\\ \hline \text{Comté de Kern } &1952 &7,7\\ \hline \text{San Francisco } &1957 &5,3\\ \hline \text{San Fernando } &1971 &6,6\\ \hline \text{LomaPrieta } &1989 &7,1\\ \hline \text{Parkfield } &2004 &6,0\\ \hline \text{Los Angeles } &2008 &5,5\\ \hline \text{Mexicali } &2010 &7,2\\ \hline \text{Napa } &2014 &6,0\\ \hline \end{array} $$ Document 2
Rappels sur la loi exponentielle
Exercice 4 5 points
Un sismologue déclare en janvier 2014 : "Le risque d'un séisme majeur le long de la faille de San Andreas, en Californie, dans les vingt prochaines années est supérieur à 70 % ".
On s'intéresse au temps, exprimé en années, écoulé entre deux séismes majeurs le long de cette faille en Californie. On admet que ce temps est une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$.
Document 1
La faille de San Andreas, en Californie : séismes majeurs de magnitude supérieure ou égale à 5. $$\begin{array}{|c|c|c|}\hline \text{Ville} & \text{Année} &\text{Magnitude}\\ \hline\hline \text{Comté d'Orange} & 1769 & 6\\ \hline \text{San Diego } &1800 & 6,5\\ \hline \text{San Francisco }&1808 &6\\ \hline \text{Fort Tejon } &1857 &8,3\\ \hline \text{Monts Santa Cruz}&1865 &6,5\\ \hline \text{Hayward } &1868 &6,9\\ \hline \text{San Francisco } &1906 &8,2\\ \hline \text{Santa Barbara } &1925 &6,3\\ \hline \text{Santa Barbara } &1927 &7,3\\ \hline \text{Long Beach } &1933 &6,3\\ \hline \text{Comté de Kern } &1952 &7,7\\ \hline \text{San Francisco } &1957 &5,3\\ \hline \text{San Fernando } &1971 &6,6\\ \hline \text{LomaPrieta } &1989 &7,1\\ \hline \text{Parkfield } &2004 &6,0\\ \hline \text{Los Angeles } &2008 &5,5\\ \hline \text{Mexicali } &2010 &7,2\\ \hline \text{Napa } &2014 &6,0\\ \hline \end{array} $$ Document 2
Rappels sur la loi exponentielle
$$\begin{array}{rl} P(X\leq 36)&= 1-P(X<36)\\ & =1- \displaystyle\int_0^{36} 0,0694 e^{-0,0694 t } \;\text{d}t \\ &= \left [ -e^{-0,0694 t }\right ]_0^{36}\\ & = 1- \left [F(36)-F(0)\right] \\ & -e^{-0,0694 \times 36 } -(-e^{0})\\ &= e^{-2,4984}\\ &\approx 0,08 \end{array}$$ La probabilité qu'il n'y ait pas d'autres séismes majeurs le long de la faille de San Andreas avant 2050 est environ 0,08.
- Vues: 23396


 $$f(-8)=f(8)=5- 0,5\left(\text{e}^{1,6} + \text{e}^{-1,6}\right)\approx 2,42$$
$$f(-8)=f(8)=5- 0,5\left(\text{e}^{1,6} + \text{e}^{-1,6}\right)\approx 2,42$$