Baccalauréat S Amérique du Sud 21 novembre 2017 - Correction Spécialité
Correction de l'exercice de Spécialité 5 points
Dans un jeu vidéo en ligne, les joueurs peuvent décider de rejoindre l'équipe A (statut noté A) ou l'équipe B (statut noté B) ou bien de n'en rejoindre aucune et rester ainsi solitaire (statut noté S). Chaque jour, chaque joueur peut changer de statut mais ne peut pas se retirer du jeu. Les données recueillies sur les premières semaines après le lancement du jeu ont permis de dégager les tendances suivantes :
- un joueur de l'équipe A y reste le jour suivant avec une probabilité de $0,6$ ; il devient joueur solitaire avec une probabilité de $0,25$. Sinon, il rejoint l'équipe B ;
- un joueur de l'équipe B y reste le jour suivant avec une probabilité de $0,6$ ; sinon, il devient joueur solitaire avec une probabilité identique à celle de rejoindre l'équipe A ;
- un joueur solitaire garde ce statut le jour suivant avec une probabilité de $\dfrac{1}{7}$ ; il rejoint l'équipe B avec une probabilité 3 fois plus élevée que celle de rejoindre l'équipe A.
Au début du jeu, à la clôture des inscriptions, tous les joueurs sont solitaires. On note $U_n = \begin{pmatrix}a_n& b_n& s_n\end{pmatrix}$ l'état probabiliste des statuts d'un joueur au bout de $n$ jours. Ainsi $a_n$ est la probabilité d'être dans l'équipe A, $b_n$ celle d'être dans l'équipe B et $s_n$ celle d'être un joueur solitaire, après $n$ jours de jeu. On a donc : $a_0 = 0$, $b_0 = 0$ et $s_0 = 1$.
- On note $p$ la probabilité qu'un joueur solitaire un jour donné passe dans l'équipe A le jour suivant. Justifier que $p = \dfrac{3}{14}$. Un joueur solitaire garde ce statut le jour suivant avec une probabilité de $\dfrac{1}{7}$;il rejoint l’équipe B avec une probabilité $3$ fois plus élevée que celle de rejoindre l’équipe A.
-
- Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.
- On admet que la matrice de transition est $T = \begin{pmatrix} \frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\ \frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix}$. Pour tout entier naturel $n$, on a donc $U_{n+1} = U_n T$. Montrer alors que, pour tout entier naturel $n$, on a $U_n = U_0T^n$. Montrons par récurrence cette propriété.
- Déterminer l'état probabiliste au bout d'une semaine, en arrondissant au millième. On a $U_1=U_0T=\begin{pmatrix} \dfrac{3}{14}&\dfrac{9}{14}&\dfrac{1}{7}\end{pmatrix}$
Initialisation : Si $n=0$ on a $U_0=U_0=U_0T^0$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $U_n=U_0T^n$
Montrons que la propriété est vraie au rang suivant, c’est-à-dire que $U_{n+1}=U_0T^{n+1}$
$\begin{align*} U_{n+1}&=U_nT\\
&=U_0TT^n\\
&=U_0T^{n+1}
\end{align*}$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a : $U_n=U_0T^n$.
$\quad$
Au bout d’une semaine on a : $a_1 \approx 0,214$, $b_1\approx 0,643$ et $s_1\approx 0,143$.
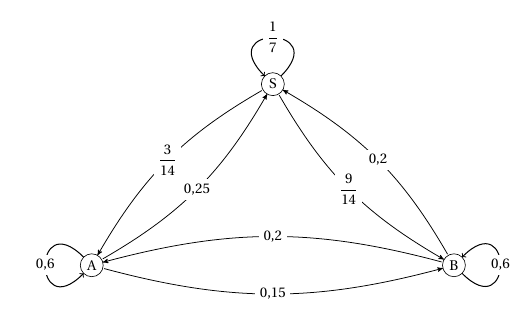
$\quad$ - Recopier et compléter le graphe probabiliste ci-dessous représentant la situation.
- On pose $V = \begin{pmatrix}300 &405 &182\end{pmatrix}$.
- Donner, sans détailler les calculs, le produit matriciel $VT$. Que constate-t-on ? On a $VT=\begin{pmatrix}300&405&182\end{pmatrix}=V$
- En déduire un état probabiliste qui reste stable d'un jour sur l'autre. L’état $V$ est donc stable d’un jour sur l’autre.
$\quad$
- On donne l'algorithme suivant, où la commande « $U[i]$ » renvoie le coefficient de la $i$-ème colonne d'une matrice ligne $U$. $$ \begin{array}{ |l|l|}\hline \text{Variables } & k \text{un entier naturel}\\ & U \text{ une matrice de taille } 1 \times 3 \\ & T \text{ une matrice carrée d'ordre } 3\\ \hline \text{Traitement } & U \text{ prend la valeur }\begin{pmatrix}0 &0 &1\end{pmatrix} \\ & T \text{ prend la valeur }\begin{pmatrix}\frac{3}{5}&\frac{3}{20}&\frac{1}{4}\\ \frac{1}{5}&\frac{3}{5}&\frac{1}{5}\\\frac{3}{14}&\frac{9}{14}&\frac{1}{7}\end{pmatrix} \\ &\text{ Pour } k \text{allant de 1 à 7}\\ &\hspace{1cm} U \text{ prend la valeur } UT \\ &\text{Fin Pour}\\ \hline \text{ Sortie }&\text{Afficher }U[1] \\ \hline \end{array} $$
- Quelle est la valeur numérique arrondie au millième de la sortie de cet algorithme ? L'interpréter dans le contexte de l'exercice. L’algorithme affiche donc $a_7 \approx 0,338$.
- Recopier et modifier cet algorithme pour qu'il affiche la fréquence de joueurs solitaires au bout de $13$ jours. On peut utilise l’algorithme suivant :
Au bout de $7$ jours, environ $33,8\%$ des joueurs sont dans l’équipe A.
$\quad$
Variables :
$\quad$ $k$ un entier naturel
$\quad$ $U$ une matrice de taille $1\times 3$
$\quad$ $T$ une matrice carrée d’ordre $3$
Traitement :
$\quad$ $U$ prend la valeur $\begin{pmatrix}0&0&1\end{pmatrix}$
$\quad$ $T$ prend la valeur $\begin{pmatrix} \dfrac{3}{5}&\dfrac{3}{20}&\dfrac{1}{4}\\
\dfrac{1}{5}&\dfrac{3}{5}&\dfrac{1}{5}\\
\dfrac{3}{14}&\dfrac{9}{14}&\dfrac{1}{7}\end{pmatrix}$
$\quad$ Pour $k$ allant de $1$ à $13$
$\qquad$ $U$ prend la valeur $UT$
$\quad$ Fin Pour
Sortie :
$\quad$ Afficher $U[3]$.
$\quad$
Cela signifie donc que :
$\begin{align*} \dfrac{1}{7}+3p+p=1 &\iff 4p=\dfrac{6}{7} \\
&\iff p=\dfrac{3}{14}
\end{align*}$
$\quad$
- Vues: 78393
