Baccalauréat S Amérique du Sud 21 novembre 2017 - Correction Exercice 1

Page 2 sur 12: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d'eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins $80$ avec $1$ litre de pâte liquide au chocolat.

Partie A : modélisation par une fonction

Le demi contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = \dfrac{x^2 - 2x - 2 - 3\ln x}{x}.\] La représentation graphique de la fonction $f$ est donnée ci-dessous.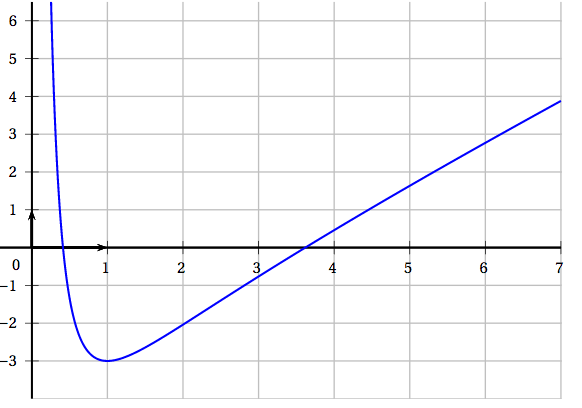

Le repère est orthogonal d'unité $2$ cm en abscisses et $1$ cm en ordonnées.

1. Soit $\varphi$ la fonction définie sur $]0~;~+ \infty[$ par : \[\varphi(x) = x^2 - 1 + 3\ln x.\]
   1. Calculer $\varphi(1)$ et la limite de $\varphi$ en $0$.
   $\varphi(1)=1^2-1+3\ln(1)=0$
   $\lim\limits_{x \to 0^+}x^2-1=-1$ et $\lim\limits_{x \to 0^+} \ln(x)=-\infty$
   Donc $\lim\limits_{x \to 0^+}\varphi(x)=-\infty$
   $\quad$
   
   2. Étudier les variations de $\varphi$ sur $]0~;~+ \infty[$. En déduire le signe de $\varphi(x)$ selon les valeurs de $x$.
   La fonction $\varphi$ est dérivable sur $]0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
   $\varphi'(x)=2x+\dfrac{3}{x} >0$ sur $]0;+\infty[$.
   La fonction $\varphi$ est donc strictement croissante sur $]0;+\infty[$.
   $\quad$
   Puisque $\varphi(1)=0$ cela signifie donc que :
   – $\varphi(x)<0$ sur l’intervalle $]0;1[$
   – $\varphi(1)=0$
   – $\varphi(x)>0$ sur l’intervalle $]1;+\infty[$
   $\quad$
2. 1. Calculer les limites de $f$ aux bornes de son ensemble de définition.
   $f(x)=\dfrac{x^2-2x-2-3\ln(x)}{x}$
   $\lim\limits_{x \to 0^+}x^2-2x-2=-2$ et $\lim\limits_{x \to 0^+} -3\ln(x)=+\infty$
   Donc $\lim\limits_{x \to 0^+} x^2-2x-2-3\ln(x)=+\infty$
   $\lim\limits_{x \to 0^+} \dfrac{1}{x}=+\infty$
   Par conséquent $\lim\limits_{x \to 0^+} f(x)=+\infty$
   $\quad$
   $f(x)=x-2-\dfrac{2}{x}-3\dfrac{\ln(x)}{x}$
   $\lim\limits_{x \to +\infty}x-2=+\infty$, $\lim\limits_{x \to +\infty} \dfrac{2}{x}=0$ et $\lim\limits_{x \to +\infty} \dfrac{\ln(x)}{x}=0$
   Donc $\lim\limits_{x \to +\infty} f(x)=+\infty$
   $\quad$
   
   2. Montrer que sur $]0~;~+ \infty[$ : $f'(x) = \dfrac{\varphi(x)}{x^2}$. En déduire le tableau de variation de $f$.
   La fonction $f$ est dérivable sur l’intervalle $]0;+\infty[$ en tant que somme et quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
   $\begin{align*} f'(x)&=\dfrac{\left(2x-2-\dfrac{3}{x}\right)x-\left(x^2-2x-2-3\ln(x)\right)}{x^2} \\
   &=\dfrac{2x^2-2x-3-x^2+2x+2+3\ln(x)}{x^2}\\
   &=\dfrac{x^2-1+3\ln(x)}{x^2}\\
   &=\dfrac{\varphi(x)}{x^2}
   \end{align*}$
   $\quad$
   
   • Signe de la dérivée :
     
   • Tableau de variations :
     
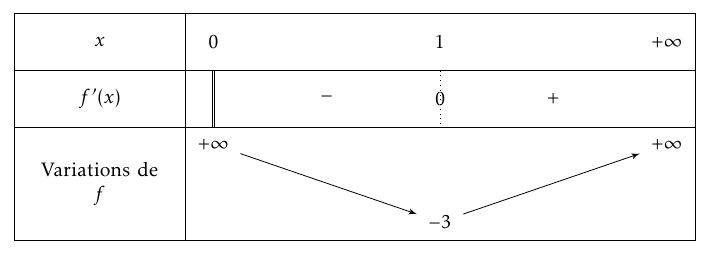
   3. Prouver que l'équation $f(x) = 0$ admet une unique solution $\alpha$ sur $]0~;~1]$. Déterminer à la calculatrice une valeur approchée de $\alpha$ à $10^{-2}$ près. On admettra que l'équation $f(x) = 0$ a également une unique solution $\beta$ sur $[1~;~+ \infty[$ avec $\beta \approx 3,61$ à $10^{-2}$ près.
   La fonction $f$ est continue (car dérivable) et strictement décroissante sur l’intervalle $]0;1]$.
   $\lim\limits_{x \to 0^+} f(x)=+\infty$ et $f(1)=-3$
   Donc $0\in[-3;+\infty[$.
   D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=0$ possède une unique solution $\alpha$ sur l’intervalle $]0;1]$.
   À l’aide de la calculatrice on trouve $\alpha\approx 0,41$
   $\quad$
   
   4. Soit $F$ la fonction définie sur $]0~;~+ \infty[$ par : \[F(x) = \dfrac{1}{2}x^2 - 2x - 2\ln x - \dfrac{3}{2}(\ln x)^2.\] Montrer que $F$ est une primitive de $f$ sur $]0~;~+ \infty[$.
   $F$ est dérivable sur l’intervalle $]0;+\infty[$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
   $\begin{align*} F'(x)&=\dfrac{1}{2}\times 2x-2-\dfrac{2}{x}-\dfrac{3}{2}\times 2\times \dfrac{1}{x}\times \ln(x) \\
   &=x-2-\dfrac{2}{x}-\dfrac{3\ln(x)}{x} \\
   &=\dfrac{x^2-2x-2-3\ln(x)}{x}\\
   &=f(x)
   \end{align*}$
   La fonction $F$ est donc une primitive de la fonction $f$ sur l’intervalle $]0;1[$.
   $\quad$

Partie B : résolution du problème

Dans cette partie, les calculs seront effectués avec les valeurs approchées à $10^{-2}$ près de $\alpha$ et $\beta$ de la partie .

La fonction $-f$ est positive sur l’intervalle $[\alpha;\beta]$.
Calculons l’aire $I$ du domaine compris entre la courbe $C’$, l’axe des abscisses et les droites d’équation $x=\alpha$ et $x=\beta$.
$\begin{align*} I&=\displaystyle \int_{\alpha}^{\beta} -f(x)\;dx \\
&=-\left(F(\beta)-F(\alpha)\right) \\
&\approx 5,598
\end{align*}$

L’aire $\mathscr{A}$ de la face supérieure est donc $2I\approx 11,196$ u.a.
Or $1$u.a. = 2 cm$^2$
Donc $\mathscr{A}\approx 22,392$ cm$^2$.

Le volume du palet est $V=\mathscr{A} \times 0,5\approx 11,196$ cm$^2$.

Par conséquent $80$ palets ont un volume de $80V\approx 895,68$ cm$^3$ (qui est bien inférieur à $1$ litre $=1~000$ cm$^3$) .

La contrainte de rentabilité est donc respectée.

$\quad$