Baccalauréat S Antilles-Guyane 11 septembre 2014 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

Partie A

---

On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~; + \infty[$ par \[f(x) = x\text{e}^{- x}.\]

1. Déterminer la limite de la fonction $f$ en $+ \infty$.
$f(x) = -\left(-x\text{e}^{-x}\right)$.
Or $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{x \to -\infty} x\text{e}^{x} = 0$.
Par conséquent $\lim\limits_{x \to +\infty} f(x) = 0$.

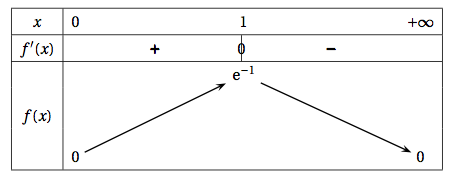
2. Déterminer la dérivée $f'$ de la fonction $f$ sur $[0~; + \infty[$ et en déduire le tableau de variations de $f$ sur $[0~; + \infty[$.
$f$ est dérivable sur $[0;+\infty[$.
$f'(x) = \text{e}^{-x} – x\text{e}^{-x} = (1-x)\text{e}^{-x}$.
La fonction exponentielle est toujours positive. Par conséquent le signe de $f'(x)$ ne dépend que de celui de $1-x$.
Or $1-x \ge 0$ $\Leftrightarrow x <1$.
On obtient ainsi le tableau de variations suivant :

---

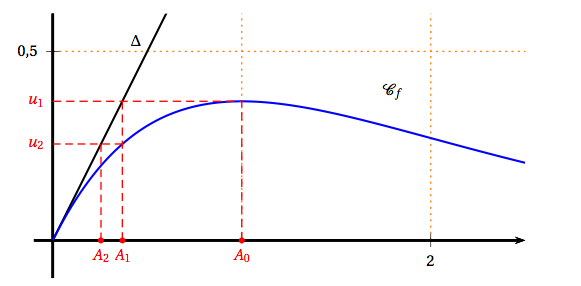
On donne en annexe la courbe $\mathcal{C}_{f}$ représentative de la fonction $f$ dans un repère du plan. La droite $\Delta$ d'équation $y = x$ a aussi été tracée.

---

Partie B

Soit la suite $\left(u_{n}\right)$ définie par $u_{0} = 1$ et, pour tout entier naturel $n,\: u_{n+1} = f\left(u_{n}\right)$.

1. Placer sur le graphique donné en annexe, en utilisant la courbe $\mathcal{C}_{f}$ et la droite $\Delta$, les points $A_{0},\, A_{1}$ et $A_{2}$ d'ordonnées nulles et d'abscisses respectives $u_{0},\, u_{1}$ et $u_{2}$. Laisser les tracés explicatifs apparents.

2. Démontrer par récurrence que pour tout entier naturel $n,\: u_{n} > 0$.
Initialisation : $u_0=1 > 0$. La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n > 0$.
On a $u_{n+1} = f(u_n) = u_n \text{e}^{-u_n}$.
La fonction exponentielle est toujours strictement positive.
Un produit de nombre strictement positif est strictement positif.
Par conséquent $u_{n+1} >0$.
$\quad$
Conclusion : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang suivant.
Par conséquent, pour tout entier naturel $n$ on a $u_n > 0$.

3. Montrer que la suite $\left(u_{n}\right)$ est décroissante.
$u_{n+1} – u_n $ $= u_n \text{-u_n} – u_n $ $= u_n\left(\text{e}^{-u_n} – 1\right)$.
D’après la question précédente, $u_n > 0$ donc $\text{e}^{-u_n}-1 <0$.
Par conséquent $u_{n+1}-u_n <0$.
La suite $(u_n)$ est donc décroissante.

4. 1. Montrer que la suite $\left(u_{n}\right)$ est convergente.
   La suite $(u_n)$ est décroissante et minorée par $0$. Elle est donc convergente.
   
   2. On admet que la limite de la suite $\left(u_{n}\right)$ est solution de l'équation $x\text{e}^{- x} = x$. Résoudre cette équation pour déterminer la valeur de cette limite.
   $x\text{e}^{-x} = x $ $\Leftrightarrow x\text{e}^{-x}-x = 0$ $ \Leftrightarrow x\left(\text{e}^{-x} -1\right) = 0$ $\Leftrightarrow x= 0$ ou $ \text{e}^{-x} – 1 = 0$ $\Leftrightarrow x=0$
   La limite de la suite $(u_n)$ est donc $0$.

---

Partie C

Déclaration des variables :
$\quad$ $S$ et $u$ sont des nombres réels
$\quad$ $k$ est un nombre entier
Initialisation :
$\quad$ $u$ prend la valeur $1$
$\quad$ $S$ prend la valeur $1$
Traitement :
$\quad$ Pour $k$ variant de $1$ à $100$
$\qquad$ $u$ prend la valeur $u\times \text{e}^{-u}$
$\qquad$ $S$ prend la valeur $S+u$
$\quad$ Fin Pour
$\quad$ Afficher $S$

$\quad$