Baccalauréat S Antilles-Guyane 11 septembre 2014
Exercice 1 6 points
Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue divers tests permettant de rejeter les peluches ne répondant pas aux normes en vigueur. D'expérience, le concepteur sait que 9$\,\%$ des nouveaux jouets ne répondent pas aux normes. A l'issue des tests, il est noté que
- 96$\,\%$ des peluches répondant aux normes sont acceptées par les tests ;
- 97$\,\%$ des peluches ne répondant pas aux normes ne sont pas acceptées à l'issue des tests.
On prélève une peluche au hasard dans la production de l'entreprise. On note
- $N$ l'évènement : « la peluche répond aux normes en vigueur » ;
- $A$ l'évènement : « la peluche est acceptée à l'issue des tests ».
Partie A
- Construire un arbre pondéré représentant la situation exposée précédemment.
- Démontrer que la probabilité qu'une peluche soit acceptée à l'issue des tests est 0,8763 .
- Calculer la probabilité qu'une peluche qui a été acceptée à l'issue des tests soit véritablement aux normes en vigueur. Arrondir le résultat au dix-millième.
Partie B
On considère que la vie d'une peluche se termine lorsqu'elle subit un dommage majeur (déchirure, arrachage ... ). On admet que la durée de vie en années d'une peluche, notée $D$, suit une loi exponentielle de paramètre $\lambda$.
- On sait que $P(D \leqslant 4) = 0,5$. Interpréter ce résultat dans le contexte de cet exercice. Calculer la valeur exacte de $\lambda$.
- On prendra ici $\lambda = 0,1733 $. Le jour de ses trois ans, un enfant qui joue avec cette peluche depuis sa naissance décide, voyant qu'elle est encore en parfait état, de la donner à sa soeur qui vient de naître. Calculer la probabilité pour que sa soeur la garde sans dommage majeur au moins cinq années supplémentaires. Arrondir le résultat au dix-millième.
Partie C
Un cabinet de sondages et d'expertise souhaite savoir quel est le réel intér êt des enfants pour ce jouet. A la suite d'une étude, il apparaît que pour un enfant de quatre ans, le nombre de jours, noté $J$, où la peluche est son jouet préféré suit une loi normale de paramètres $\mu$ et $\sigma$. Il apparaît que $\mu = 358$ jours.
- Soit $X = \frac{J - 358}{\sigma}$. Quelle est la loi suivie par $X$ ?
- On sait que $P(J \leqslant 385) = 0,975$. Déterminer la valeur de $\sigma$ arrondie à l'entier le plus proche.
Correction de l'exercice 1 (6 points)
Une entreprise de jouets en peluche souhaite commercialiser un nouveau produit et à cette fin, effectue divers tests permettant de rejeter les peluches ne répondant pas aux normes en vigueur. D'expérience, le concepteur sait que 9$\,\%$ des nouveaux jouets ne répondent pas aux normes. A l'issue des tests, il est noté que
- 96$\,\%$ des peluches répondant aux normes sont acceptées par les tests ;
- 97$\,\%$ des peluches ne répondant pas aux normes ne sont pas acceptées à l'issue des tests.
On prélève une peluche au hasard dans la production de l'entreprise. On note
- $N$ l'évènement : « la peluche répond aux normes en vigueur » ;
- $A$ l'évènement : « la peluche est acceptée à l'issue des tests ».
Partie A
- Construire un arbre pondéré représentant la situation exposée précédemment.
- Démontrer que la probabilité qu'une peluche soit acceptée à l'issue des tests est 0,8763 . D’après la formule des probabilités totales, on a :
- Calculer la probabilité qu'une peluche qui a été acceptée à l'issue des tests soit véritablement aux normes en vigueur. Arrondir le résultat au dix-millième. On veut calculer $p_A(N) = \dfrac{p(A\cap N)}{p(A)}$ $=\dfrac{0,91 \times 0,96}{0,8763}$ $\approx 0,9969$
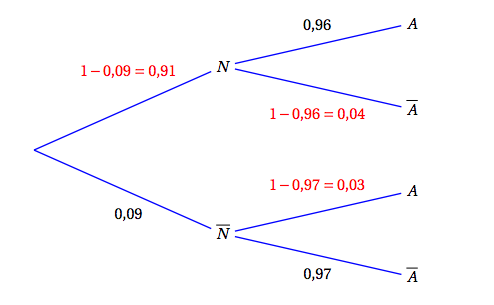
$$\begin{array} {ll}p(A) &= p(N \cap A) + p\left(\overline{N} \cap A \right) \\ &= 0,91 \times 0,96 + 0,09 \times 0,03 \\ &= 0,8763 \end{array}$$
Partie B
On considère que la vie d'une peluche se termine lorsqu'elle subit un dommage majeur (déchirure, arrachage ... ). On admet que la durée de vie en années d'une peluche, notée $D$, suit une loi exponentielle de paramètre $\lambda$.
- On sait que $P(D \leqslant 4) = 0,5$. Interpréter ce résultat dans le contexte de cet exercice. Calculer la valeur exacte de $\lambda$. $P(D \le 4) = 0,5$ signifie que la probabilité qu’une peluche « vive » moins de $4$ ans est de $0,5$.
- On prendra ici $\lambda = 0,1733 $. Le jour de ses trois ans, un enfant qui joue avec cette peluche depuis sa naissance décide, voyant qu'elle est encore en parfait état, de la donner à sa soeur qui vient de naître. Calculer la probabilité pour que sa soeur la garde sans dommage majeur au moins cinq années supplémentaires. Arrondir le résultat au dix-millième. On veut calculer $P_{D\ge 3}(D \ge 8) $ $=P_{D \ge 3}(D \ge 3 + 5)$ $=P(D \ge 5)$ $= \text{e}^{-5\lambda}$ $\approx 0,4204$ (durée de vie sans vieillissement).
$\quad$
On a ainsi $1- \text{e}^{-4\lambda} = 0,5$ $\Leftrightarrow -4\lambda = \ln 0,5$ $\Leftrightarrow \lambda = -\dfrac{ \ln 0,5}{4}$
Partie C
- Soit $X = \frac{J - 358}{\sigma}$. Quelle est la loi suivie par $X$ ? Puisque $X=\dfrac{J-\mu}{\sigma}$, $X$ suit la loi normale centrée réduite.
- On sait que $P(J \leqslant 385) = 0,975$. Déterminer la valeur de $\sigma$ arrondie à l'entier le plus proche. $$\begin{array}{ll} P(J \le 385) = 0,975 & \Leftrightarrow P(J – 358 \le 27) = 0,975 \\ & P\left(\dfrac{J – 385}{\sigma} \le \dfrac{27}{\sigma}\right) = 0,975 \\ \end{array}$$
Par conséquent, en utilisant la calculatrice, on obtient $\dfrac{27}{\sigma} \approx 1,96$ et $\sigma \approx 14$.
Exercice 2 6 points
Partie A
On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~; + \infty[$ par \[f(x) = x\text{e}^{- x}.\]
- Déterminer la limite de la fonction $f$ en $+ \infty$.
- Déterminer la dérivée $f'$ de la fonction $f$ sur $[0~; + \infty[$ et en déduire le tableau de variations de $f$ sur $[0~; + \infty[$.
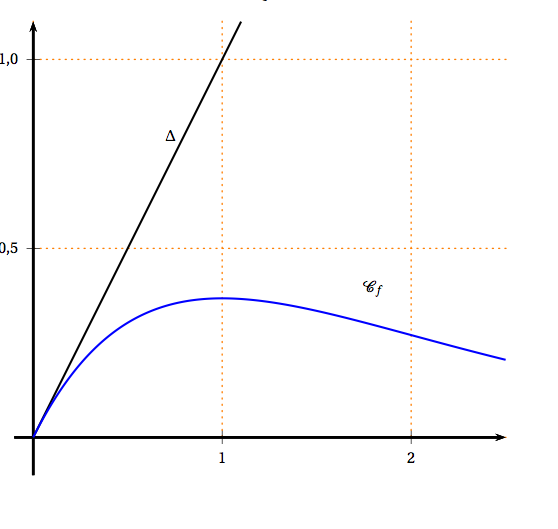
On donne en annexe la courbe $\mathcal{C}_{f}$ représentative de la fonction $f$ dans un repère du plan. La droite $\Delta$ d'équation $y = x$ a aussi été tracée.
Partie B
Soit la suite $\left(u_{n}\right)$ définie par $u_{0} = 1$ et, pour tout entier naturel $n,\: u_{n+1} = f\left(u_{n}\right)$.
- Placer sur le graphique donné en annexe, en utilisant la courbe $\mathcal{C}_{f}$ et la droite $\Delta$, les points $A_{0},\, A_{1}$ et $A_{2}$ d'ordonnées nulles et d'abscisses respectives $u_{0},\, u_{1}$ et $u_{2}$. Laisser les tracés explicatifs apparents.
- Démontrer par récurrence que pour tout entier naturel $n,\: u_{n} > 0$.
- Montrer que la suite $\left(u_{n}\right)$ est décroissante.
-
- Montrer que la suite $\left(u_{n}\right)$ est convergente.
- On admet que la limite de la suite $\left(u_{n}\right)$ est solution de l'équation $x\text{e}^{- x} = x$. Résoudre cette équation pour déterminer la valeur de cette limite.
Partie C
On considère la suite $\left(S_{n}\right)$ définie pour tout entier naturel $n$ par \[S_{n} = \displaystyle\sum_{k= 0}^{k=n} u_{k} = u_{0} + u_{1} + \cdots + u_{n}.\] Compléter l'algorithme donné en annexe afin qu'il calcule $S_{100}$.
Annexe 1 Exercice 2 Partie B , question 1
Annexe 2 Exercice 2 Partie C
$$\begin{array}{|l|}\hline \text{ Déclaration des variables :}\\ \hspace{1cm}\begin{array}{l} S \text{ et } u \text{ sont des nombres réels}\\ k \text{ est un nombre entier} \end{array}\\ \text{Initialisation : }\\ \hspace{1cm}\begin{array}{l} u \text{ prend la valeur } \ldots \ldots\\ S \text{ prend la valeur }\ldots \ldots\\ \end{array}\\ \text{ Traitement : }\\\hspace{1cm} \begin{array}{l} \text{Pour } k \text{ variant de 1 à } \ldots.\\\hspace{1cm} \begin{array}{l} u \text{ prend la valeur } u \times \text{e}^{- u}\\ S \text{ prend la valeur } \ldots.\\ \end{array}\\ \text{Fin Pour }\\ \text{ Afficher } \ldots \ldots\\ \end{array}\\ \hline \end{array}$$
Correction de l'exercice 2 (6 points)
Partie A
On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~; + \infty[$ par \[f(x) = x\text{e}^{- x}.\]
- Déterminer la limite de la fonction $f$ en $+ \infty$. $f(x) = -\left(-x\text{e}^{-x}\right)$.
- Déterminer la dérivée $f'$ de la fonction $f$ sur $[0~; + \infty[$ et en déduire le tableau de variations de $f$ sur $[0~; + \infty[$. $f$ est dérivable sur $[0;+\infty[$.
Or $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{x \to -\infty} x\text{e}^{x} = 0$.
Par conséquent $\lim\limits_{x \to +\infty} f(x) = 0$.
$f'(x) = \text{e}^{-x} – x\text{e}^{-x} = (1-x)\text{e}^{-x}$.
La fonction exponentielle est toujours positive. Par conséquent le signe de $f'(x)$ ne dépend que de celui de $1-x$.
Or $1-x \ge 0$ $\Leftrightarrow x <1$.
On obtient ainsi le tableau de variations suivant :
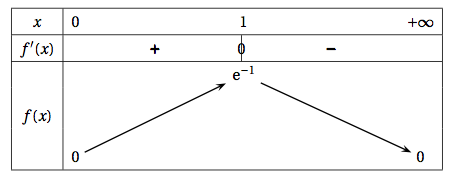
On donne en annexe la courbe $\mathcal{C}_{f}$ représentative de la fonction $f$ dans un repère du plan. La droite $\Delta$ d'équation $y = x$ a aussi été tracée.
Partie B
Soit la suite $\left(u_{n}\right)$ définie par $u_{0} = 1$ et, pour tout entier naturel $n,\: u_{n+1} = f\left(u_{n}\right)$.
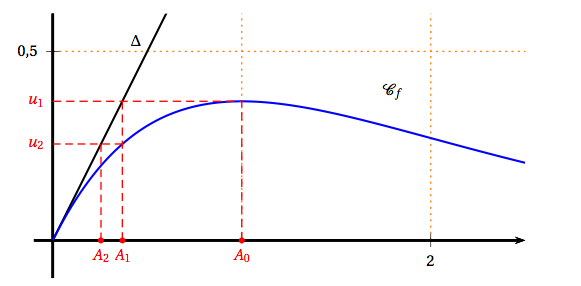
- Placer sur le graphique donné en annexe, en utilisant la courbe $\mathcal{C}_{f}$ et la droite $\Delta$, les points $A_{0},\, A_{1}$ et $A_{2}$ d'ordonnées nulles et d'abscisses respectives $u_{0},\, u_{1}$ et $u_{2}$. Laisser les tracés explicatifs apparents.
- Démontrer par récurrence que pour tout entier naturel $n,\: u_{n} > 0$. Initialisation : $u_0=1 > 0$. La propriété est donc vraie au rang $0$.
- Montrer que la suite $\left(u_{n}\right)$ est décroissante. $u_{n+1} – u_n $ $= u_n \text{-u_n} – u_n $ $= u_n\left(\text{e}^{-u_n} – 1\right)$.
-
- Montrer que la suite $\left(u_{n}\right)$ est convergente. La suite $(u_n)$ est décroissante et minorée par $0$. Elle est donc convergente.
- On admet que la limite de la suite $\left(u_{n}\right)$ est solution de l'équation $x\text{e}^{- x} = x$. Résoudre cette équation pour déterminer la valeur de cette limite. $x\text{e}^{-x} = x $ $\Leftrightarrow x\text{e}^{-x}-x = 0$ $ \Leftrightarrow x\left(\text{e}^{-x} -1\right) = 0$ $\Leftrightarrow x= 0$ ou $ \text{e}^{-x} – 1 = 0$ $\Leftrightarrow x=0$
La limite de la suite $(u_n)$ est donc $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n > 0$.
On a $u_{n+1} = f(u_n) = u_n \text{e}^{-u_n}$.
La fonction exponentielle est toujours strictement positive.
Un produit de nombre strictement positif est strictement positif.
Par conséquent $u_{n+1} >0$.
$\quad$
Conclusion : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang suivant.
Par conséquent, pour tout entier naturel $n$ on a $u_n > 0$.
D’après la question précédente, $u_n > 0$ donc $\text{e}^{-u_n}-1 <0$.
Par conséquent $u_{n+1}-u_n <0$.
La suite $(u_n)$ est donc décroissante.
Partie C
On considère la suite $\left(S_{n}\right)$ définie pour tout entier naturel $n$ par \[S_{n} = \displaystyle\sum_{k= 0}^{k=n} u_{k} = u_{0} + u_{1} + \cdots + u_{n}.\] Compléter l'algorithme donné en annexe afin qu'il calcule $S_{100}$.
Annexe 2 Exercice 2 Partie C
$$\begin{array}{|l|}\hline \text{ Déclaration des variables :}\\ \hspace{1cm}\begin{array}{l} S \text{ et } u \text{ sont des nombres réels}\\ k \text{ est un nombre entier} \end{array}\\ \text{Initialisation : }\\ \hspace{1cm}\begin{array}{l} u \text{ prend la valeur } \ldots \ldots\\ S \text{ prend la valeur }\ldots \ldots\\ \end{array}\\ \text{ Traitement : }\\\hspace{1cm} \begin{array}{l} \text{Pour } k \text{ variant de 1 à } \ldots.\\\hspace{1cm} \begin{array}{l} u \text{ prend la valeur } u \times \text{e}^{- u}\\ S \text{ prend la valeur } \ldots.\\ \end{array}\\ \text{Fin Pour }\\ \text{ Afficher } \ldots \ldots\\ \end{array}\\ \hline \end{array}$$
Déclaration des variables :
$\quad$ $S$ et $u$ sont des nombres réels
$\quad$ $k$ est un nombre entier
Initialisation :
$\quad$ $u$ prend la valeur $1$
$\quad$ $S$ prend la valeur $1$
Traitement :
$\quad$ Pour $k$ variant de $1$ à $100$
$\qquad$ $u$ prend la valeur $u\times \text{e}^{-u}$
$\qquad$ $S$ prend la valeur $S+u$
$\quad$ Fin Pour
$\quad$ Afficher $S$
$\quad$
Exercice 3 3 points
On considère l'équation $\left(E_{1}\right)$ : \[\text{e}^x - x^n = 0\] où $x$ est un réel strictement positif et $n$ un entier naturel non nul.
- Montrer que l'équation $\left(E_{1}\right)$ est équivalente à l'équation $\left(E_{2}\right)$ : \[\ln (x) - \dfrac{x}{n} = 0.\]
- Pour quelles valeurs de $n$ l'équation $\left(E_{1}\right)$ admet-elle deux solutions ?
Correction de l'exercice 3 (3 points)
On considère l'équation $\left(E_{1}\right)$ : \[\text{e}^x - x^n = 0\] où $x$ est un réel strictement positif et $n$ un entier naturel non nul.
- Montrer que l'équation $\left(E_{1}\right)$ est équivalente à l'équation $\left(E_{2}\right)$ : \[\ln (x) - \dfrac{x}{n} = 0.\] $$\begin{array} {ll}\text{e}^x – x^n = 0 &\Leftrightarrow \text{e}^x=x^n \\ &\Leftrightarrow x = n \ln (x) \\ &\Leftrightarrow \ln(x) = \dfrac{x}{n} \\ &\Leftrightarrow \ln(x) – \dfrac{x}{n} = 0 \end{array}$$
- Pour quelles valeurs de $n$ l'équation $\left(E_{1}\right)$ admet-elle deux solutions ? Soit $f_n$ la fonction définie sur $]0;+\infty[$ par $f_n(x)=\ln(x) – \dfrac{x}{n}$.
Cette fonction est dérivable sur $]0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
$f_n'(x) = \dfrac{1}{x} – \dfrac{1}{n}= \dfrac{n}{nx} – \dfrac{x}{nx}=\dfrac{n-x}{nx}$.
On travaille sur $]0; +\infty[$, donc $x>0$, par ailleurs $n$ est un entier strictement positif;
Ainsi $f_n'(x)$ a le signe de $n-x$. $f_n'(x) >0 \Leftrightarrow x < n$.
On obtient ainsi le tableau de variations suivant :
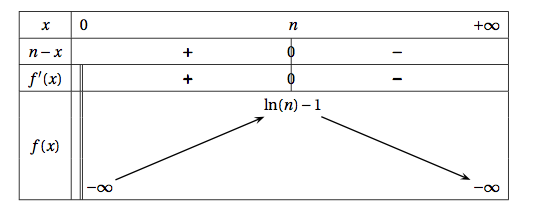
$\lim\limits_{x \to 0} \ln(x) = -\infty$ donc $\lim\limits_{x \to 0} f_n(x) = -\infty$
$f(x) = x\left(\dfrac{\ln(x)}{x} – \dfrac{1}{n} \right)$.
Or $\lim\limits_{x \to +\infty} \dfrac{\ln(x)}{x} = 0$ donc $\lim\limits_{x \to +\infty} f_n(x) = -\infty$.
$\quad$
$\ln n -1 > 0 \Leftrightarrow n > \text{e}$.
Par conséquent si $n \le 2$, $f_n(x) < 0$ et l’équation $(E_2)$ n’aura pas de solution.
Si $n \ge 3$, la fonction $f_n$ est dérivable sur $]0;+\infty[$ donc continue .
Sur $]0;n[$ la fonction est strictement croissante.
$\lim\limits_{x \to 0} f_n(x) =-\infty$ et $f_n(n) >0$.
D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $f_n(x) = 0$ possède une unique solution.
$\quad$
Sur $]n;+\infty[$, la fonction $f_n$ est strictement décroissante.
$f_n(n) >0$ et $\lim\limits_{x \to +\infty} f_n(x) = -\infty$.
D’après le théorème de la bijection l’équation $f_n(x)=0$ possède une unique solution.
$\quad$
Par conséquent l’équation $(E_2)$, et donc $(E_1)$ possède deux solutions si, et seulement si, $n \ge 3$
Exercice 4 5 points
On note $\mathbb C$ l'ensemble des nombres complexes. Le plan complexe est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. On prendra comme unité 2 cm sur chaque axe.
Le graphique sera fait sur une feuille de papier millimétré et complété au fur et à mesure des questions.
On considère la fonction $f$ qui à tout nombre complexe $z$ associe \[f(z) = z^2 + 2z + 9.\]
- Calculer l'image de $- 1 + \text{i}\sqrt{3}$ par la fonction $f$.
- Résoudre dans $\mathbb C$ l'équation $f(z) = 5$. Ecrire sous forme exponentielle les solutions de cette équation. Construire alors sur le graphique, à la règle et au compas, les points A et B dont l'affixe est solution de l'équation (A étant le point dont l'affixe a une partie imaginaire positive). On laissera les traits de construction apparents.
- Soit $\lambda$ un nombre réel. On considère l'équation $f(z) = \lambda$ d'inconnue $z$. Déterminer l'ensemble des valeurs de $\lambda$ pour lesquelles l'équation $f(z) = \lambda$ admet deux solutions complexes conjuguées.
- Soit (F) l'ensemble des points du plan complexe dont l'affixe $z$ vérifie \[|f(z) - 8| = 3.\] Prouver que (F) est le cercle de centre $\Omega(-1~;~0)$ et de rayon $\sqrt{3}$. Tracer (F) sur le graphique.
- Soit $z$ un nombre complexe, tel que $z = x + \text{i}y$ où $x$ et $y$ sont des nombres réels.
- Montrer que la forme algébrique de $f(z)$ est \[x^2 - y^2 + 2x + 9 + \text{i}(2xy + 2y).\]
- On note (E) l'ensemble des points du plan complexe dont l'affixe $z$ est telle que $f(z)$ soit un nombre réel. Montrer que (E) est la réunion de deux droites $D_{1}$ et $D_{2}$ dont on précisera les équations. Compléter le graphique de l'annexe en traà§ant ces droites.
- Déterminer les coordonnées des points d'intersection des ensembles (E) et (F).
Correction de l'exercice 4 5 points
On note $\mathbb C$ l'ensemble des nombres complexes. Le plan complexe est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. On prendra comme unité 2 cm sur chaque axe.
Le graphique sera fait sur une feuille de papier millimétré et complété au fur et à mesure des questions.
On considère la fonction $f$ qui à tout nombre complexe $z$ associe \[f(z) = z^2 + 2z + 9.\]
- Calculer l'image de $- 1 + \text{i}\sqrt{3}$ par la fonction $f$. $$\begin{array}{ll} f\left(-1+\text{i}\sqrt{3}\right) &= \left(-1 + \text{i}\sqrt{3}\right)^2 + 2\left(-1 + \text{i}\sqrt{3}\right) + 9 \\ &=1 -2\sqrt{3}\text{i} – 3 – 2 +\sqrt{3}\text{i} + 9 \\ &= 5 \end{array}$$
- Résoudre dans $\mathbb C$ l'équation $f(z) = 5$. Ecrire sous forme exponentielle les solutions de cette équation. Construire alors sur le graphique, à la règle et au compas, les points A et B dont l'affixe est solution de l'équation (A étant le point dont l'affixe a une partie imaginaire positive). On laissera les traits de construction apparents. $f(x) = 5 \Leftrightarrow z^2+2z+4 = 0$
- Soit $\lambda$ un nombre réel. On considère l'équation $f(z) = \lambda$ d'inconnue $z$. Déterminer l'ensemble des valeurs de $\lambda$ pour lesquelles l'équation $f(z) = \lambda$ admet deux solutions complexes conjuguées. $f(z)=\lambda$ $\Leftrightarrow z^2+2z+9-\lambda$
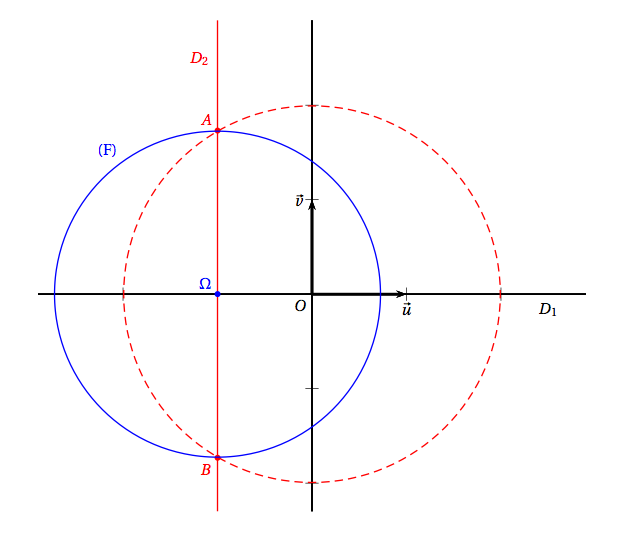
- Soit (F) l'ensemble des points du plan complexe dont l'affixe $z$ vérifie \[|f(z) - 8| = 3.\] Prouver que (F) est le cercle de centre $\Omega(-1~;~0)$ et de rayon $\sqrt{3}$. Tracer (F) sur le graphique. $|f(z)-8|=|z^2 + 2z + 1| $ $= \left|(z+1)^2\right|$ $ = |z+1|^2$.
- Soit $z$ un nombre complexe, tel que $z = x + \text{i}y$ où $x$ et $y$ sont des nombres réels.
- Montrer que la forme algébrique de $f(z)$ est \[x^2 - y^2 + 2x + 9 + \text{i}(2xy + 2y).\] $$\begin{array}{ll} f(x+\text{i}y) &= \left(x+\text{i}y\right)^2+2(x+\text{i}y) + 9 \\ &= x^2+2xy\text{i} – y^2 + 2x + 2y\text{i} + 9 \\ &= x^2-y^2+2x + 9 + \text{i}(2xy+2y) \end{array}$$
- On note (E) l'ensemble des points du plan complexe dont l'affixe $z$ est telle que $f(z)$ soit un nombre réel. Montrer que (E) est la réunion de deux droites $D_{1}$ et $D_{2}$ dont on précisera les équations. Compléter le graphique de l'annexe en traà§ant ces droites. $f(z)$ est nombre réel si, et seulement si, $2xy+2y=0$ $\Leftrightarrow 2y(x+1)=0$ $\Leftrightarrow y = 0$ ou $x=-1$.
$(E)$ est donc la réunion des droites d’équation $y=0$ et $x=-1$. - Déterminer les coordonnées des points d'intersection des ensembles (E) et (F). Regardons dans un premier temps l’intersection de $(F)$ avec $D_1$ d’équation $y=0$.
$\Delta = 2^- 4 \times 4 = -12$
Il y a donc deux racines complexes : $z_1 = \dfrac{-2 -\text{i}\sqrt{12}}{2} = -1 – \text{i}\sqrt{3}$ et $z_2 = \overline{z_1} = -1 + \text{i}\sqrt{3}$
$|z_1| = \sqrt{1 + 3} = 2$.
Donc $z_1 = 2\left(-\dfrac{1}{2} – \dfrac{\sqrt{3}}{2}\text{i}\right) = 2\text{e}^{-2\text{i}\pi/3}$ et $z_2 = 2\text{e}^{2\text{i}\pi/3}$
$\quad$
$\Delta = 2^2 – 4(9-\lambda) $ $= 4 – 36 + 4\lambda$ $=4(-8 + \lambda)$.
L’équation $f(z)=\lambda$ possède donc deux solutions complexes conjuguées si, et seulement si, $\lambda <8$.
Par conséquent $|f(z)-8|3 \Leftrightarrow |z+1| = \sqrt{3}$.
$(F)$ est donc bien le cercle de centre $\Omega(-1;0)$ et de rayon $\sqrt{3}$.
Il s’agit donc de deux points d’abscisse respective $-1 – \sqrt{3}$ et $1+\sqrt{3}$. On a donc $C\left(-1-\sqrt{3};0\right)$ et $D\left(-1+\sqrt{3};0\right)$.
$\quad$
Regardons maintenant l’intersection de $(F)$ avec la droite $D_2$ d’équation $x=-1$.
Il s’agit de deux points d’ordonnée respective $0+\sqrt{3}$ et $0-\sqrt{3}$. On a donc $G\left(-1;\sqrt{3}\right)$ et $H\left(-1;-\sqrt{3}\right)$.
Spécialité 5 points
Dans une ville, une enseigne de banque nationale possède deux agences, appelées X et Y. D'une année sur l'autre, une partie des fonds de l'agence X est transférée à l'agence Y, et réciproquement. De plus, chaque année, le siège de la banque transfère une certaine somme à chaque agence.
Soit $n$ un entier naturel. On note $x_{n}$ la quantité de fonds détenue par l'agence X, et $y_{n}$ la quantité de fonds détenue par l'agence Y au 1er janvier de l'année $2014 + n$, exprimées en millions d'euros. On note $U_{n}$ la matrice $\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix}$ et on note $I = \begin{pmatrix}1&0\\0&1\end{pmatrix}$. On suppose que le 1er janvier de l'année 2014, l'agence X possède 50 millions d'euros et l'agence Y possède 10 millions d'euros. L'évolution de la quantité de fonds est régie par la relation suivante : \[U_{n+1} = AU_{n} + B,\: \text{où}\:\: A = \begin{pmatrix}0,6&0,15\\0,2&0,4\end{pmatrix} \:\:\text{et}\:\ B = \begin{pmatrix}1\\3\end{pmatrix}.\]
- Interpréter dans le contexte de l'exercice le coefficient 0,6 de la matrice $A$ et le coefficient 3 de la matrice $B$.
- Donner la matrice $U_{0}$ puis calculer la quantité de fonds détenue par chacune des agences X et Y en 2015, exprimée en millions d'euros.
- On note $D = \begin{pmatrix}0,3&0\\0&0,7\end{pmatrix},\: P = \begin{pmatrix}1&3\\- 2&2\end{pmatrix}$ et $Q = \begin{pmatrix}0,25&- 0,375\\0,25 &0,125\end{pmatrix}$.
- Donner sans détailler le calcul, la matrice $P DQ$.
- Expliciter le calcul du coefficient de la première ligne et de la deuxième colonne du produit matriciel $QP$. Dans la suite, on admettra que $QP = I$.
On admettra dans la suite de cet exercice que pour tout entier naturel non nul $n,$ $A^n = P D^nQ$. - On pose pour tout entier naturel $n,\: V_{n} = U_{n} - \begin{pmatrix}5\\20/3\end{pmatrix}$.
- Démontrer que pour tout entier naturel $n,\: V_{n+1} = AV_{n}$.
- Déterminer $V_{0}$ puis pour tout entier naturel $n$, donner l'expression de $V_{n}$ en fonction de $A,\, n$ et $V_{0}$.
- Soit $n$ un entier naturel. On admet que \[A^n = \begin{pmatrix}0,25 \times 0,3^n + 0,75 \times 0,7^n&0,375\left(- 0,3^n + 0,7^n\right)\\ 0,5\left(- 0,3^n + 0,7^n\right)& 0,75 \times 0,3^n + 0,25 \times 0,7^n\end{pmatrix}.\]
- Déterminer le coefficient de la première ligne de la matrice $V_{n}$ en détaillant les calculs.
- En déduire l'expression de $x_{n}$ en fonction de $n$.
- Déterminer la limite de $x_{n}$ quand $n$ tend vers $+ \infty$ et interpréter ce résultat dans le cadre du problème.
Correction de l'exercice de Spécialité 5 points
Dans une ville, une enseigne de banque nationale possède deux agences, appelées X et Y. D'une année sur l'autre, une partie des fonds de l'agence X est transférée à l'agence Y, et réciproquement. De plus, chaque année, le siège de la banque transfère une certaine somme à chaque agence.
Soit $n$ un entier naturel. On note $x_{n}$ la quantité de fonds détenue par l'agence X, et $y_{n}$ la quantité de fonds détenue par l'agence Y au 1er janvier de l'année $2014 + n$, exprimées en millions d'euros. On note $U_{n}$ la matrice $\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix}$ et on note $I = \begin{pmatrix}1&0\\0&1\end{pmatrix}$. On suppose que le 1er janvier de l'année 2014, l'agence X possède 50 millions d'euros et l'agence Y possède 10 millions d'euros. L'évolution de la quantité de fonds est régie par la relation suivante : \[U_{n+1} = AU_{n} + B,\: \text{où}\:\: A = \begin{pmatrix}0,6&0,15\\0,2&0,4\end{pmatrix} \:\:\text{et}\:\ B = \begin{pmatrix}1\\3\end{pmatrix}.\]
- Interpréter dans le contexte de l'exercice le coefficient 0,6 de la matrice $A$ et le coefficient 3 de la matrice $B$. L’agence $X$ conserve $60\%$ de ses fonds d’une année sur l’autre.
- Donner la matrice $U_{0}$ puis calculer la quantité de fonds détenue par chacune des agences X et Y en 2015, exprimée en millions d'euros. $U_0=\begin{pmatrix} 50 \\\\10 \end{pmatrix}$.
- On note $D = \begin{pmatrix}0,3&0\\0&0,7\end{pmatrix},\: P = \begin{pmatrix}1&3\\- 2&2\end{pmatrix}$ et $Q = \begin{pmatrix}0,25&- 0,375\\0,25 &0,125\end{pmatrix}$.
- Donner sans détailler le calcul, la matrice $P DQ$. $PDQ = \begin{pmatrix} 0,6&0,15 \\\\0,2&0,4 \end{pmatrix} = A$.
- Expliciter le calcul du coefficient de la première ligne et de la deuxième colonne du produit matriciel $QP$. Dans la suite, on admettra que $QP = I$. Ce coefficient est obtenu à partir du calcul suivant : $0,25 \times 3 – 0,375 \times (2) = 0$
On admettra dans la suite de cet exercice que pour tout entier naturel non nul $n,$ $A^n = P D^nQ$. - On pose pour tout entier naturel $n,\: V_{n} = U_{n} - \begin{pmatrix}5\\20/3\end{pmatrix}$.
- Démontrer que pour tout entier naturel $n,\: V_{n+1} = AV_{n}$. $$\begin{array}{ll} V_{n+1} &= U_{n+1} – \begin{pmatrix} 5 \\ 20/3 \end{pmatrix} \\ &= AU_n+B – \begin{pmatrix} 5 \\ 20/3 \end{pmatrix} \\ &=AU_n + \begin{pmatrix} -4 \\ -11/3 \end{pmatrix} \end{array}$$
- Déterminer $V_{0}$ puis pour tout entier naturel $n$, donner l'expression de $V_{n}$ en fonction de $A,\, n$ et $V_{0}$. $V_0 = \begin{pmatrix} = 45 \\ 10/3 \end{pmatrix}$.
Or $A\begin{pmatrix} -5 \\-20/3 \end{pmatrix} = \begin{pmatrix} -4 \\-11/3 \end{pmatrix}$
Donc $V_{n+1}=AV_n$.
On a ainsi $V_n = A^nV_0$ pour tout $n \in \mathbb N$. - Soit $n$ un entier naturel. On admet que \[A^n = \begin{pmatrix}0,25 \times 0,3^n + 0,75 \times 0,7^n&0,375\left(- 0,3^n + 0,7^n\right)\\ 0,5\left(- 0,3^n + 0,7^n\right)& 0,75 \times 0,3^n + 0,25 \times 0,7^n\end{pmatrix}.\]
- Déterminer le coefficient de la première ligne de la matrice $V_{n}$ en détaillant les calculs. Ce coefficient est donné par :
- En déduire l'expression de $x_{n}$ en fonction de $n$. On a ainsi $x_n = 10 \times 0,3^n+35\times 0,7^n + 5$
- Déterminer la limite de $x_{n}$ quand $n$ tend vers $+ \infty$ et interpréter ce résultat dans le cadre du problème. $-1<0,3<1$ et $-1<0,7<1$.
$$\begin{array}{ll} v &= 45(0,25\times 0,3^n+0,75 \times 0,7^n) + \dfrac{10}{3}\left[0,375(-0,3^n+0,7^n)\right] \\ &= 10 \times 0,3^n+35\times 0,7^n \end{array}$$
Par conséquent $\lim\limits_{n \to +\infty} 0,3^n = \lim\limits_{n \to +\infty} 0,7^n = 0$.
Donc $\lim\limits_{n \to +\infty} x_n = 5$.
Au bout d’un grand nombre d’année, les fonds disponibles de l’agence X seront de $5$ millions d’euros.
$\quad$
Chaque année le siège de la banque transfère $3$ millions d’euros à l’agence $Y$.
- Vues: 35763
