Baccalauréat S Amérique du Nord 30 mai 2014 - Correction Exercice 3

Page 6 sur 11: Correction Exercice 3

Exercice 3 4 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Partie A : Section du cube par le plan (MNP)

1. Justifier que les droites (MP) et (FG) sont sécantes en un point L.Construire le point L

Dans le plan $(EFG)$, les droites $(PM)$ et $(FG)$ ne sont pas parallèles, elles sont donc sécantes; on appelle $L$ leur point d'intersection.
2. On admet que les droites (LN) et (CG) sont sécantes et on note T leur point d'intersection.
   On admet que les droites (LN) et (BF) sont sécantes et on note Q leur point d'intersection.
   Construire les points T et Q en laissant apparents les traits de construction.

Les droites $(LN)$, $(BF)$ et $(CG)$ sont coplanaires dans le plan $(BCG)$ d'où les constructions de $T$ et $Q$.
3. Construire l'intersection des plans (MNP) et (ABF).
$$ \left. \begin{array}{r} \left. \begin{array}{r} \left. \begin{array}{r} L \in (MP) \Longrightarrow L \in (MNP)\\ N \in (MNP) \end{array} \right\rbrace \Longrightarrow (LN) \subset (MNP)\\ Q \in (LN) \end{array} \right\rbrace \Longrightarrow Q \in (MNP)\\[15pt] Q \in [BF] \Longrightarrow Q \in (ABF) \end{array} \right\rbrace \Longrightarrow Q \in (MNP) \cap (ABF) $$ Les droites $(MP)$ et $(EF)$ du plan $(EFG)$ ne sont pas parallèles, donc elles sont sécantes; on appelle $R$ leur point d'intersection. $$ \left. \begin{array}{r} R \in (MP) \Longrightarrow R \in (MNP)\\ R \in (EF) \Longrightarrow R \in (ABF) \end{array} \right\rbrace \Longrightarrow R \in (MNP) \cap (ABF) $$ Les plans $(MNP)$ et $(ABF)$ ont deux points en commun, $Q$ et $R$; ils ne sont pas confondus car $P \in (MNP)$ et $P \not\in (ABF)$. Ces deux plans sont donc sécants et comme $Q$ et $R$ appartiennent aux deux plans, l'intersection des deux plans $(MNP)$ et $(ABF)$ est la droite $(QR)$.


4. En déduire une construction de la section du cube par le plan (MNP).

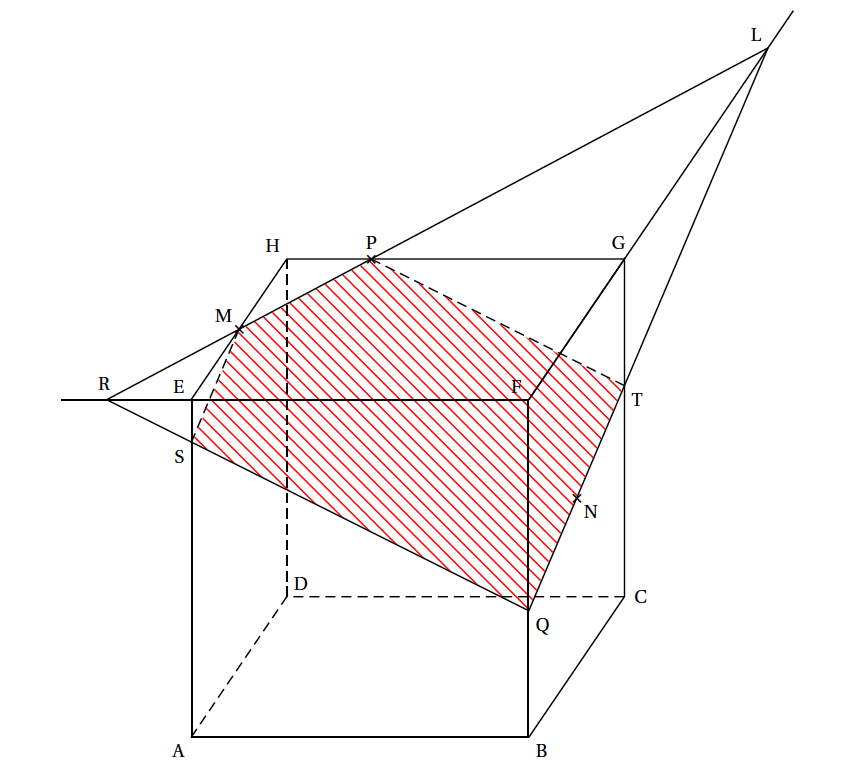
Notons $S$ le point d'intersection de $(AE)$ et $(QR)$. La section du cube par le plan $(MNP)$ est le pentagone $MPTQS$.

  Partie B

L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.

1. Donner les coordonnées des points M, N et P dans ce repère.

Coordonnées: $M$ est le milieu du segment $[EH]$ donc $M$ a pour coordonnées $\left (\dfrac{0+0}{2}~;~\dfrac{0+1}{2}~;~\dfrac{1+1}{2}\right ) =\left (0~;~\dfrac{1}{2}~;~1\right )$;
$N$ est le milieu du segment $[FC]$ donc $n$ a pour coordonnées $\left (\dfrac{1+1}{2}~;~\dfrac{0+1}{2}~;~\dfrac{1+0}{2}\right ) = \left (1~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$ ;
$P(x~;~y~;~z)$ vérifie $\overrightarrow{HP}=\dfrac{1}{4} \overrightarrow{HG}$, on a donc: $ \left\lbrace \begin{array}{l l} x-0 =& \dfrac{1}{4}\\ y-1 =& 0\\ z-1= & 0 \end{array} \right. \iff \left\lbrace \begin{array}{l l} x=& \dfrac{1}{4}\\ y=& 1\\ z=& 1 \end{array} \right.$ Donc $P \left (\dfrac{1}{4}\,;\, 1 \,;\, 1\right )$.
2. Déterminer les coordonnées du point L.

Pour calculer les coordonnées du point $L$, on écrit les systèmes de représentations paramétriques des droites $(MP)$ et $(FG)$.
$(MP)$ passe par $M \left(0~;~\dfrac{1}{2}~;~1 \right) $ et a pour vecteur directeur $ \vec{MP} \left(\dfrac{1}{4}~;~\dfrac{1}{2}~;~0 \right) $.
Une représentation paramétrique de cette droite est donc : $\left\lbrace \begin{array}{l l l} x =& \dfrac{1}{4}k &\\[8pt] y =& \dfrac{1}{2} + \dfrac{1}{2} k & \text{où } k \in \mathbb{R} \\[8pt] z= & 1 & \end{array} \right. $
$(FG)$ passe par $F \left(1~;~0~;~1 \right) $ et a pour vecteur directeur $ \vec{FG} \left(0~;~1~;~0 \right)$.
Une représentation paramétrique de cette droite est donc : $ \left\lbrace \begin{array}{l l l} x =& 1 &\\ y= & k' & \text{où } k' \in \mathbb{R} \\ z =& 1 & \end{array} \right.$
On détermine l'intersection de ces deux droites: $$ \left\lbrace\begin{array}{l l} \dfrac{1}{4}k &=& 1\\[8pt] \dfrac{1}{2}+\dfrac{1}{2}k &=& k'\\[5pt] 1 &=& 1 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l l l} k =& 4\\[5pt] k'= & \dfrac{5}{2} \end{array}\right. $$
Donc le point $L$ a pour coordonnées $\left (1\,;\,\dfrac{5}{2}\,;\,1\right )$.
3. On admet que le point T a pour coordonnées $\left(1~;~1~;~\frac{5}{8}\right)$.
   Le triangle TPN est-il rectangle en T ?

On calcule le produit scalaire $\overrightarrow{TP}.\overrightarrow{TN}$ $$ \overrightarrow{TP}\begin{pmatrix}-\dfrac{3}{4}\\0\\\dfrac{3}{8}\end{pmatrix}.\overrightarrow{TN}\begin{pmatrix}0\\-\dfrac{1}{2}\\-\dfrac{1}{8}\end{pmatrix}= -\dfrac{3}{4}\times 0+0\times \left(-\dfrac{1}{2}\right)+\dfrac{3}{8}\times \left(-\dfrac{1}{8}\right)\not= 0 $$
Le triangle $TPN$ n'est pas rectangle en $T$.