Baccalauréat S Amérique du Nord 30 mai 2014

Exercice 1 5 points

Commun à  tous les candidats
 
Dans cet exercice, tous les résultats demandés seront arrondis à $10^{-3}$  près.
  Une grande enseigne de cosmétiques lance une nouvelle crème hydratante.
  Partie A : Conditionnement des pots
  Cette enseigne souhaite vendre la nouvelle crème sous un conditionnement de 50 mL et dispose pour ceci de pots de contenance maximale 55 mL. On dit qu'un pot de crème est non conforme s'il contient moins de 49 mL de crème.

1. Plusieurs séries de tests conduisent à modéliser la quantité de crème, exprimée en mL, contenue dans chaque pot par une variable aléatoire $X$ qui suit la loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma = 1,2$. Calculer la probabilité qu'un pot de crème soit non conforme.
2. La proportion de pots de crème non conformes est jugée trop importante. En modifiant la viscosité de la crème, on peut changer la valeur de l'écart-type de la variable aléatoire $X$, sans modifier son espérance $\mu = 50$.
   On veut réduire à $0,06$ la probabilité qu'un pot choisi au hasard soit non conforme. On note $\sigma'$ le nouvel écart-type, et $Z$ la variable aléatoire égale à $\dfrac{X - 50}{\sigma'}$
   1. Préciser la loi que suit la variable aléatoire $Z$.
   2. Déterminer une valeur approchée du réel $u$ tel que $p(Z \leqslant u) = 0, 06$.
   3. En déduire la valeur attendue de $\sigma'$.
3. Une boutique commande à son fournisseur 50 pots de cette nouvelle crème. On considère que le travail sur la viscosité de la crème a permis d'atteindre l'objectif fixé et donc que la proportion de pots non conformes dans l'échantillon est $0,06$. Soit $Y$ la variable aléatoire égale au nombre de pots non conformes parmi les 50 pots reçus.
   1. On admet que $Y$ suit une loi binomiale. En donner les paramètres.
   2. Calculer la probabilité que la boutique reçoive deux pots non conformes ou moins de deux pots non conformes.

  Partie B : Campagne publicitaire
  Une association de consommateurs décide d'estimer la proportion de personnes satisfaites par l'utilisation de cette crème. Elle réalise un sondage parmi les personnes utilisant ce produit. Sur $140$ personnes interrogées, $99$ se déclarent satisfaites. Estimer, par intervalle de confiance au seuil de $95$ %, la proportion de personnes satisfaites parmi les utilisateurs de la crème.

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

1. Plusieurs séries de tests conduisent à modéliser la quantité de crème, exprimée en mL, contenue dans chaque pot par une variable aléatoire $X$ qui suit la loi normale d'espérance $\mu = 50$ et d'écart-type $\sigma = 1,2$. Calculer la probabilité qu'un pot de crème soit non conforme.

On veut $p(X \leqslant 49) $. Avec la calculatrice $p(X \leqslant 49) \approx 0.202 $.
2nd   DISTR   2 NormalFRép( $-10^{99}$  , 49,50,1.2)EXE 
2. La proportion de pots de crème non conformes est jugée trop importante. En modifiant la viscosité de la crème, on peut changer la valeur de l'écart-type de la variable aléatoire $X$, sans modifier son espérance $\mu = 50$.
   
   On veut réduire à $0,06$ la probabilité qu'un pot choisi au hasard soit non conforme. On note $\sigma'$ le nouvel écart-type, et $Z$ la variable aléatoire égale à $\dfrac{X - 50}{\sigma'}$
   1. Préciser la loi que suit la variable aléatoire $Z$.
   
   La variable aléatoire $Z$ suit la loi normale centrée réduite. En effet si $X$ suit $\mathcal{N}(\mu,\sigma)$ alors $Z= \dfrac{X - \mu}{\sigma}$ suit $\mathcal{N}(0,1)$
   $Z$ suit la loi normale centrée réduite.
   2. Déterminer une valeur approchée du réel $u$ tel que $p(Z \leqslant u) = 0, 06$.
   
   Une valeur approchée du réel $u$ tel que $p(Z \leqslant u) = 0, 06$ est $u \approx -1.555$.
   $p(Z \leqslant u) = 0, 06 \Longleftrightarrow \pi(u)=0, 06 \Longleftrightarrow u= \pi^{-1}(0, 06)$
   2nd   DISTR   3 FracNormale( 0.06 ) EXE 
   3. En déduire la valeur attendue de $\sigma'$.
   
   
   • Première méthode :
     $ Z = \dfrac{X - 50}{\sigma'} \Leftrightarrow X = \sigma' Z + 50 $ $ p(X \leqslant 49) =0,06 \Leftrightarrow p\left(\sigma' Z + 50 \leqslant 49 \right) =0,06 \Leftrightarrow p \left( Z \leqslant -\dfrac{1}{\sigma'} \right) =0,06 $ On doit donc avoir $ -\dfrac{1}{\sigma'} = -1,555 \Leftrightarrow \sigma' = \dfrac{1}{1,555} \approx 0,643$ La valeur attendue de $\sigma'$ est donc $ 0,643 $.
   • Deuxième méthode :
     $ p(X \leqslant 49) =0,06 \Leftrightarrow p\left(\dfrac{X - 50}{\sigma'}\leqslant \dfrac{49 - 50}{\sigma'} \right) =0,06  (1) $
     $(1) \Leftrightarrow p\left(Z\leqslant -\dfrac{1}{\sigma'} \right) =0,06 \Leftrightarrow \pi\left(-\dfrac{1}{\sigma'}\right)=0, 06 \Longleftrightarrow -\dfrac{1}{\sigma'}= \pi^{-1}(0, 06)\Leftrightarrow \sigma' =-\dfrac{1}{\pi^{-1}(0, 06)} $
     La valeur attendue de $\sigma'$ est donc $ 0,643 $.
     
3. Une boutique commande à son fournisseur 50 pots de cette nouvelle crème. On considère que le travail sur la viscosité de la crème a permis d'atteindre l'objectif fixé et donc que la proportion de pots non conformes dans l'échantillon est $0,06$. Soit $Y$ la variable aléatoire égale au nombre de pots non conformes parmi les 50 pots reçus.
   1. On admet que $Y$ suit une loi binomiale. En donner les paramètres.
   
   Ici, l'épreuve de Bernoulli consiste à tester si un pot est non conforme considéré comme succès de probabilité $0,06$,... ou pas. On répète $50$ fois cette épreuve de façon indépendante. $Y$ suit donc la loi binomiale de paramètres $50$ et $0,06$.
   $Y$ suit donc la loi binomiale $\mathcal{B}(50;0,06)$
   2. Calculer la probabilité que la boutique reçoive deux pots non conformes ou moins de deux pots non conformes.
   
   On calcule $ p(Y \leqslant 2) $ :
   • avec la calculatrice:
   • On a pour tout $k \in [0;50]; p(Y=k)=\binom{50}{k}\times 0,06^k \times 0,94^{50-k}$
     $ p(Y \leqslant 2) =p(Y=0)+p(Y=1)+p(Y=2) \approx 0,416$
   La probabilité que la boutique reçoive deux pots non conformes ou moins de deux pots non conformes est d'environ $ 0,416 $.

  Partie B : Campagne publicitaire
  Une association de consommateurs décide d'estimer la proportion de personnes satisfaites par l'utilisation de cette crème. Elle réalise un sondage parmi les personnes utilisant ce produit. Sur $140$ personnes interrogées, $99$ se déclarent satisfaites.

On a $ n= 140 > 30, \quad f = \dfrac{99}{140} $ donc $ nf = 99 > 5 $ et $ n(1-f) = 41 > 5 $. Ainsi, $ \left[f - \dfrac{1}{\sqrt{n}} ; f + \dfrac{1}{\sqrt{n}} \right] $ soit $ \left[0,622 ; 0,792 \right] $ est donc un intervalle de confiance au seuil de $95$ % de la proportion de personnes satisfaites parmi les utilisateurs de la crème.

Exercice 2 6 points

Commun à  tous les candidats
 
On considère la fonction $f$ définie sur $[0~;~+\infty[$ par
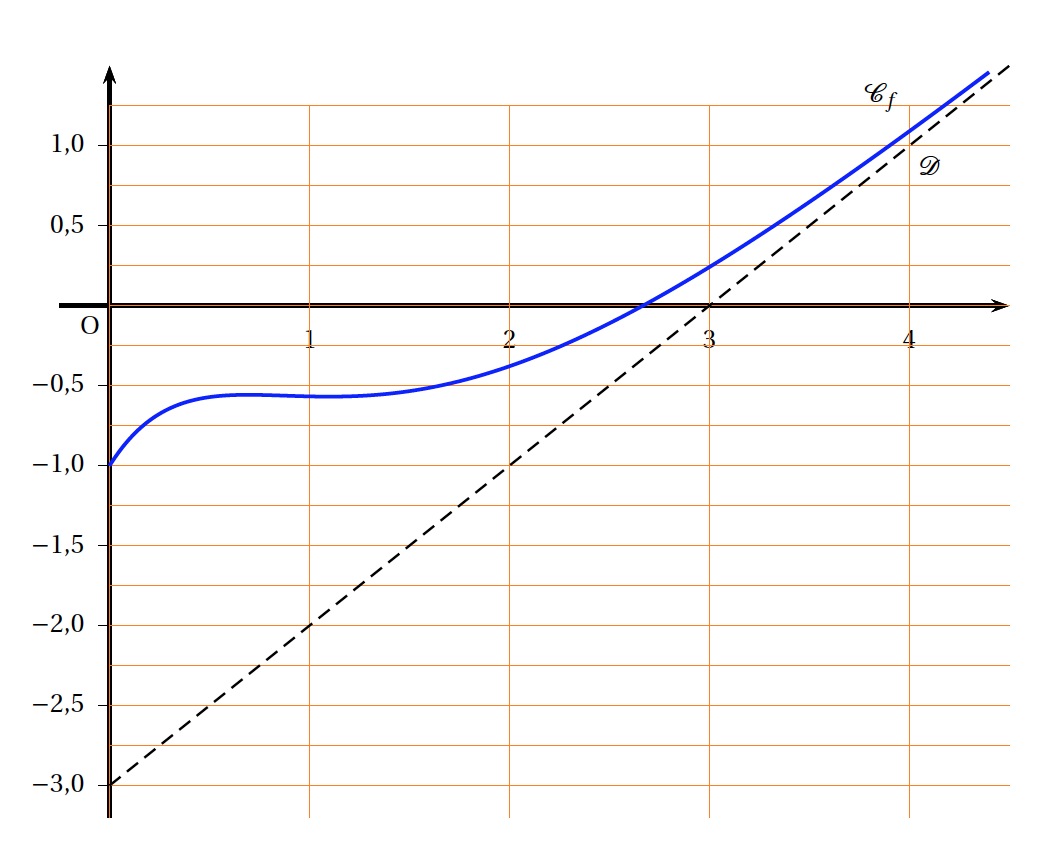
\[f(x) = 5 \text{e}^{-x} - 3\text{e}^{-2x} + x - 3.\] On note $\mathcal{C}_{f}$ la représentation graphique de la fonction $f$ et $\mathcal{D}$ la droite d'équation $y = x - 3$ dans un repère orthogonal du plan.
  Partie A : Positions relatives de $\mathcal{C}_{f}$ et $\mathcal{D}$
  Soit $g$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par $g(x) = f(x) - (x - 3)$.

1. Justifier que, pour tout réel $x$ de l'intervalle $[0~;~+\infty[$,  $g(x) > 0$.
2. La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ ont-elles un point commun ? Justifier.

  Partie B : Étude de la fonction $g$ On note $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}_{f}$, $N$ le point d'abscisse $x$ de la droite $\mathcal{D}$ et on s'intéresse à l'évolution de la distance $MN$.

1. Justifier que, pour tout $x$ de l'intervalle $[0~;~+\infty[$, la distance $MN$ est égale à $g(x)$.
2. On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0~;~+\infty[$.
   Pour tout $x$ de l'intervalle $[0~;~+\infty[$, calculer $g'(x)$.
3. Montrer que la fonction $g$ possède un maximum sur l'intervalle $[0~;~+\infty[$ que l'on déterminera.
   En donner une interprétation graphique.

    Partie C : Étude d'une aire
  On considère la fonction $\mathcal{A}$ définie sur l'intervalle $[0~;~+\infty[$ par
\[\mathcal{A}(x) = \displaystyle\int_{0}^x [f(t) - (t - 3)]\: \text{d}t.\]

1. Hachurer sur le graphique donné en  annexe 1 (à rendre avec la copie)  le domaine dont l'aire est donnée par $\mathcal{A}(2)$.
2. Justifier que la fonction $\mathcal{A}$ est croissante sur l'intervalle $[0~;~+\infty[$.
3. Pour tout réel $x$ strictement positif, calculer $\mathcal{A}(x)$.
4. Existe-t-il une valeur de $x$ telle que $\mathcal{A}(x) = 2$ ?

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

  Partie A : Positions relatives de $\mathcal{C}_{f}$ et $\mathcal{D}$
  Soit $g$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par $g(x) = f(x) - (x - 3)$.

1. Justifier que, pour tout réel $x$ de l'intervalle $[0~;~+\infty[$,  $g(x) > 0$.


Pour tout réel $x$ de l'intervalle $[0~;~+\infty[$,
$g(x)= 5 \text{e}^{-x} - 3\text{e}^{-2x} = \text{e}^{-x} \left( 5 - 3 \text{e}^{-x} \right) $. Comme $\text{e}^{-x}>0$ (exponentielle), $g(x)$ est du signe de $5 - 3 \text{e}^{-x} $. $5 - 3 \text{e}^{-x} > 0 \Leftrightarrow 5 > 3\text{e}^{-x} \Leftrightarrow \dfrac{5}{3} > \text{e}^{-x} \Leftrightarrow \ln \left( \dfrac{5}{3} \right) >-x \Leftrightarrow \ln \left( \dfrac{3}{5} \right) < x$ ce qui est toujours vrai car $\ln \left( \dfrac{3}{5} \right)<0<x$

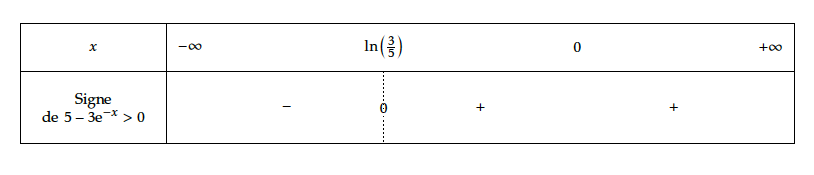
Finalement, pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, $g(x)>0$.
2. La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ ont-elles un point commun ? Justifier.

La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ ont un point commun d'abscisse $x$ si et seulement si $ f(x) = x-3$ soit $ g(x) = 0 $ ce qui n'est pas possible car on vient de voir que $g(x) > 0$.
La courbe $\mathcal{C}_{f}$ et la droite $\mathcal{D}$ n'ont pas de point commun.

  Partie B : Étude de la fonction $g$ On note $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}_{f}$, $N$ le point d'abscisse $x$ de la droite $\mathcal{D}$ et on s'intéresse à l'évolution de la distance $MN$.

1. Justifier que, pour tout $x$ de l'intervalle $[0~;~+\infty[$, la distance $MN$ est égale à $g(x)$.

Comme $M$ et $N$ ont la même abscisse, pour tout $x$ de l'intervalle $[0~;~+\infty[ $, $MN = \mid f(x) - (x-3) \mid = \mid g(x) \mid = g(x) $ car $g(x) >0$ d'après la première question.
2. On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0~;~+\infty[$.
   Pour tout $x$ de l'intervalle $[0~;~+\infty[$, calculer $g'(x)$.

On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0~;~+\infty[$. Si $u$ est dérivable,$\left( \text{e}^{u}\right)' = u' \text{e}^{u} $. La dérivée de $ x \mapsto \text{e}^{-x} $ est donc $ x \mapsto -\text{e}^{-x} $ et celle de $ x\mapsto \text{e}^{-2x} $ est $ x \mapsto -2 \text{e}^{-2x} $.
Pour tout $x$ de l'intervalle $[0~;~+\infty[$, $g'(x) =- 5 \text{e}^{-x} + 2 \times 3 \text{e}^{-2x} = 6\text{e}^{-2x} -5\text{e}^{-x}$.
3. Montrer que la fonction $g$ possède un maximum sur l'intervalle $[0~;~+\infty[$ que l'on déterminera.
   En donner une interprétation graphique.

$g$ étant dérivable sur $[0~;~+\infty[$, on étudie le signe de sa dérivée sur $[0~;~+\infty[$. Pour tout $x$ de l'intervalle $[0~;~+\infty[$, $$\begin{array}{lll} g'(x) \geqslant 0 & \Leftrightarrow 6\text{e}^{-2x} -5\text{e}^{-x} \geqslant 0 & \\ & \Leftrightarrow 6 \text{e}^{-x} -5 \geqslant 0 & \text{on a divisé par } \text{e}^{-x}>0 \\[5pt] & \Leftrightarrow \text{e}^{-x} \geqslant \dfrac{5}{6} & \\[5pt] & \Leftrightarrow - x \geqslant \ln \left( \dfrac{5}{6} \right)& \text{croissance de la fonction } \ln \\[8pt] & \Leftrightarrow x \leqslant \ln \left( \dfrac{6}{5} \right) \\ \end{array}$$ En $ \ln \left( \dfrac{6}{5} \right) $, la dérivée s'annule en changeant de signe $ (+ ; -) $, donc $g\left( \ln \left( \dfrac{6}{5} \right)\right) $ est un maximum pour $g$ sur l'intervalle $[0~;~+\infty[$. $g\left( \ln \left( \dfrac{6}{5} \right)\right) = 5 \times \text{e}^{\frac{5}{6}}-3 \times \left( \text{e}^{\frac{5}{6}}\right)^2 = 5 \times \dfrac{5}{6} - 3 \times \left( \dfrac{5}{6}\right)^2 = \dfrac{75}{36} = \dfrac{25}{12}$.
La distance entre un point de la courbe $\mathcal{C}_{f}$ et le point de même abscisse sur la droite $\mathcal{D}$ est donc maximale lorsque $ x = \ln \left( \dfrac{6}{5} \right) $. Cette distance maximale vaut $ \dfrac{25}{12}$  unités.
Remarque : Comme le repère est orthogonal (a priori pas orthonormé), il s'agit d'unité en ordonnée.)

    Partie C : Étude d'une aire
  On considère la fonction $\mathcal{A}$ définie sur l'intervalle $[0~;~+\infty[$ par
\[\mathcal{A}(x) = \displaystyle\int_{0}^x [f(t) - (t - 3)]\: \text{d}t.\]

1. Hachurer sur le graphique donné en  annexe 1 (à rendre avec la copie)  le domaine dont l'aire est donnée par $\mathcal{A}(2)$.


2. Justifier que la fonction $\mathcal{A}$ est croissante sur l'intervalle $[0~;~+\infty[$.

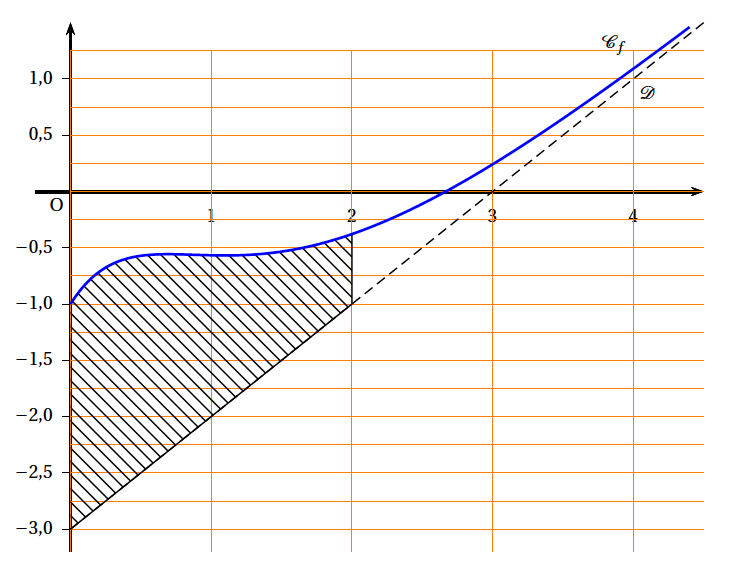
La fonction $g$ est continue sur $ [0 ; +\infty [ $ et $ \mathcal{A}(x) = \displaystyle\int_{0}^x g(t)\text{d}t $, la fonction $ \mathcal{A} $ est donc dérivable sur $ [0 ; +\infty [ $ et $ \mathcal{A}' = g >0 $. La fonction $\mathcal{A}$ est donc bien croissante sur l'intervalle $[0~;~+\infty[$
3. Pour tout réel $x$ strictement positif, calculer $\mathcal{A}(x)$.

Pour tout réel $x$ strictement positif, $$ \begin{array}{lll} \mathcal{A}(x) & = \displaystyle\int_{0}^x g(t)\text{d}t & \\[8pt] &= 5\displaystyle\int_{0}^x \text{e}^{-t} \text{d}t - 3\displaystyle\int_{0}^x \text{e}^{-2t} \text{d}t & \text{ par linéarité de l'intégrale} \\[8pt] & = 5\displaystyle \left[-\text{e}^{-t} \right]_0^x -3\displaystyle \left[-\dfrac{1}{2}\text{e}^{-2t} \right]_0^x \\[8pt] &= 5\left( -\text{e}^{-x} +1 \right) - 3 \left( -\dfrac{1}{2}\text{e}^{-2x} + \dfrac{1}{2} \right) & \\[8pt] & = 5 - 5 \text{e}^{-x}+ \dfrac{3}{2}\text{e}^{-2x} -\dfrac{3}{2} \\[8pt] \mathcal{A}(x)& = \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{7}{2} \end{array} $$
4. Existe-t-il une valeur de $x$ telle que $\mathcal{A}(x) = 2$ ?


$\mathcal{A}(x) = 2 \Leftrightarrow \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{7}{2} = 2 \Leftrightarrow \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{3}{2} = 0$ On pose $ X = \text{e}^{-x} $

$$\begin{array}{lll} x \text{ solution de } \dfrac{3}{2}\text{e}^{-2x}- 5 \text{e}^{-x} +\dfrac{3}{2} = 0 & \Leftrightarrow X \text{ solution de } \dfrac{3}{2}X^2 - 5 X + \dfrac{3}{2}= 0 & \\ &\Leftrightarrow X \text{ solution de } 3X^2-10X+3=0 & \text{ équation du second degré} \\ &\Leftrightarrow X = \dfrac{1}{3} \text{ ou } X = 3 &\\ &\Leftrightarrow \text{e}^{-x} =\dfrac{1}{3} \text{ ou } \text{e}^{-x} = 3 & \text{on revient à } x \text{ et } X = \text{e}^{-x} \\ &\Leftrightarrow x = \ln 3 \text{ ou } x = - \ln 3 & - \ln \dfrac{1}{3} = -(-\ln 3) = \ln 3 \\ &\Leftrightarrow x = \ln 3 & \text{car } x \geqslant 0 \text{ et }-\ln 3 \text{ est strictement négatif } \end{array} $$
Finalement, $\mathcal{A}(x) = 2 \Leftrightarrow x = \ln 3$.

Exercice 3 4 points

Commun à  tous les candidats

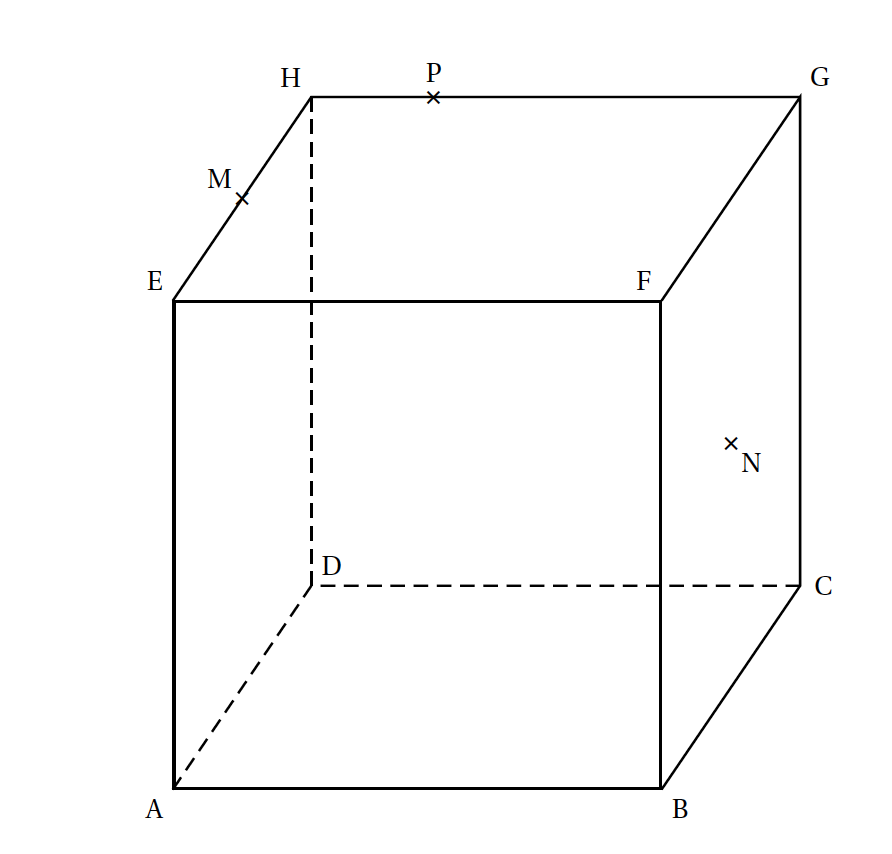
On considère un cube ABCDEFCH donné en annexe 2 (à rendre avec la copie). On note M le milieu du segment [EH], N celui de [FC] et P le point tel que $\vec{\text{HP}} = \dfrac{1}{4} \vec{\text{HG}}$.
Partie A : Section du cube par le plan (MNP)

1. Justifier que les droites (MP) et (FG) sont sécantes en un point L.Construire le point L
2. On admet que les droites (LN) et (CG) sont sécantes et on note T leur point d'intersection.
3. Construire l'intersection des plans (MNP) et (ABF).
4. En déduire une construction de la section du cube par le plan (MNP).

  Partie B

L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.

1. Donner les coordonnées des points M, N et P dans ce repère.
2. Déterminer les coordonnées du point L.
3. On admet que le point T a pour coordonnées $\left(1~;~1~;~\frac{5}{8}\right)$.
   Le triangle TPN est-il rectangle en T ?

Exercice 3 4 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Partie A : Section du cube par le plan (MNP)

1. Justifier que les droites (MP) et (FG) sont sécantes en un point L.Construire le point L

Dans le plan $(EFG)$, les droites $(PM)$ et $(FG)$ ne sont pas parallèles, elles sont donc sécantes; on appelle $L$ leur point d'intersection.
2. On admet que les droites (LN) et (CG) sont sécantes et on note T leur point d'intersection.
   On admet que les droites (LN) et (BF) sont sécantes et on note Q leur point d'intersection.
   Construire les points T et Q en laissant apparents les traits de construction.

Les droites $(LN)$, $(BF)$ et $(CG)$ sont coplanaires dans le plan $(BCG)$ d'où les constructions de $T$ et $Q$.
3. Construire l'intersection des plans (MNP) et (ABF).
$$ \left. \begin{array}{r} \left. \begin{array}{r} \left. \begin{array}{r} L \in (MP) \Longrightarrow L \in (MNP)\\ N \in (MNP) \end{array} \right\rbrace \Longrightarrow (LN) \subset (MNP)\\ Q \in (LN) \end{array} \right\rbrace \Longrightarrow Q \in (MNP)\\[15pt] Q \in [BF] \Longrightarrow Q \in (ABF) \end{array} \right\rbrace \Longrightarrow Q \in (MNP) \cap (ABF) $$ Les droites $(MP)$ et $(EF)$ du plan $(EFG)$ ne sont pas parallèles, donc elles sont sécantes; on appelle $R$ leur point d'intersection. $$ \left. \begin{array}{r} R \in (MP) \Longrightarrow R \in (MNP)\\ R \in (EF) \Longrightarrow R \in (ABF) \end{array} \right\rbrace \Longrightarrow R \in (MNP) \cap (ABF) $$ Les plans $(MNP)$ et $(ABF)$ ont deux points en commun, $Q$ et $R$; ils ne sont pas confondus car $P \in (MNP)$ et $P \not\in (ABF)$. Ces deux plans sont donc sécants et comme $Q$ et $R$ appartiennent aux deux plans, l'intersection des deux plans $(MNP)$ et $(ABF)$ est la droite $(QR)$.


4. En déduire une construction de la section du cube par le plan (MNP).

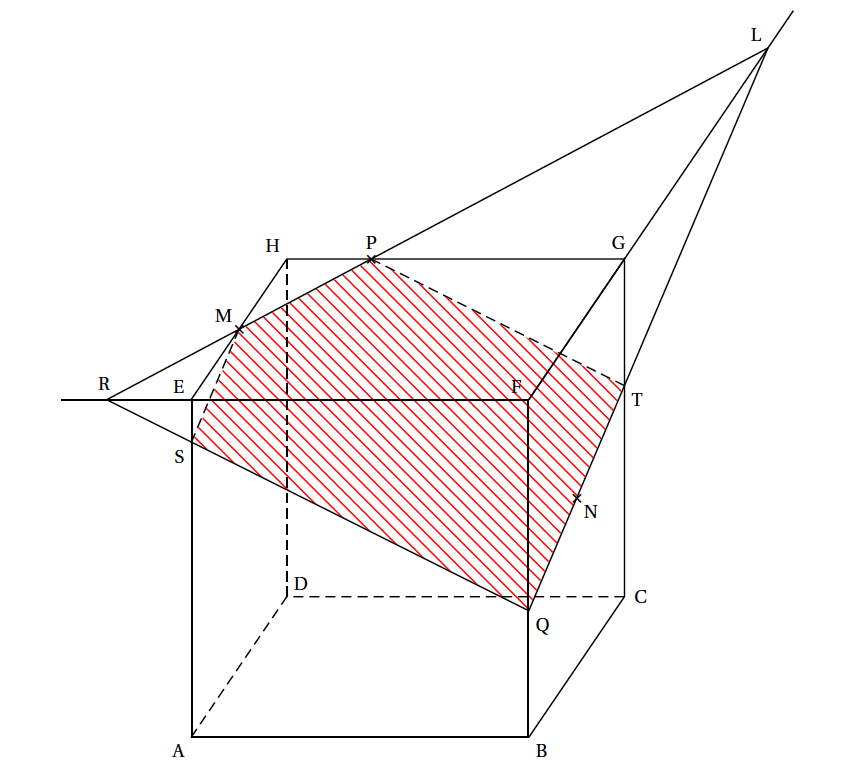
Notons $S$ le point d'intersection de $(AE)$ et $(QR)$. La section du cube par le plan $(MNP)$ est le pentagone $MPTQS$.

  Partie B

L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.

1. Donner les coordonnées des points M, N et P dans ce repère.

Coordonnées: $M$ est le milieu du segment $[EH]$ donc $M$ a pour coordonnées $\left (\dfrac{0+0}{2}~;~\dfrac{0+1}{2}~;~\dfrac{1+1}{2}\right ) =\left (0~;~\dfrac{1}{2}~;~1\right )$;
$N$ est le milieu du segment $[FC]$ donc $n$ a pour coordonnées $\left (\dfrac{1+1}{2}~;~\dfrac{0+1}{2}~;~\dfrac{1+0}{2}\right ) = \left (1~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$ ;
$P(x~;~y~;~z)$ vérifie $\overrightarrow{HP}=\dfrac{1}{4} \overrightarrow{HG}$, on a donc: $ \left\lbrace \begin{array}{l l} x-0 =& \dfrac{1}{4}\\ y-1 =& 0\\ z-1= & 0 \end{array} \right. \iff \left\lbrace \begin{array}{l l} x=& \dfrac{1}{4}\\ y=& 1\\ z=& 1 \end{array} \right.$ Donc $P \left (\dfrac{1}{4}\,;\, 1 \,;\, 1\right )$.
2. Déterminer les coordonnées du point L.

Pour calculer les coordonnées du point $L$, on écrit les systèmes de représentations paramétriques des droites $(MP)$ et $(FG)$.
$(MP)$ passe par $M \left(0~;~\dfrac{1}{2}~;~1 \right) $ et a pour vecteur directeur $ \vec{MP} \left(\dfrac{1}{4}~;~\dfrac{1}{2}~;~0 \right) $.
Une représentation paramétrique de cette droite est donc : $\left\lbrace \begin{array}{l l l} x =& \dfrac{1}{4}k &\\[8pt] y =& \dfrac{1}{2} + \dfrac{1}{2} k & \text{où } k \in \mathbb{R} \\[8pt] z= & 1 & \end{array} \right. $
$(FG)$ passe par $F \left(1~;~0~;~1 \right) $ et a pour vecteur directeur $ \vec{FG} \left(0~;~1~;~0 \right)$.
Une représentation paramétrique de cette droite est donc : $ \left\lbrace \begin{array}{l l l} x =& 1 &\\ y= & k' & \text{où } k' \in \mathbb{R} \\ z =& 1 & \end{array} \right.$
On détermine l'intersection de ces deux droites: $$ \left\lbrace\begin{array}{l l} \dfrac{1}{4}k &=& 1\\[8pt] \dfrac{1}{2}+\dfrac{1}{2}k &=& k'\\[5pt] 1 &=& 1 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l l l} k =& 4\\[5pt] k'= & \dfrac{5}{2} \end{array}\right. $$
Donc le point $L$ a pour coordonnées $\left (1\,;\,\dfrac{5}{2}\,;\,1\right )$.
3. On admet que le point T a pour coordonnées $\left(1~;~1~;~\frac{5}{8}\right)$.
   Le triangle TPN est-il rectangle en T ?

On calcule le produit scalaire $\overrightarrow{TP}.\overrightarrow{TN}$ $$ \overrightarrow{TP}\begin{pmatrix}-\dfrac{3}{4}\\0\\\dfrac{3}{8}\end{pmatrix}.\overrightarrow{TN}\begin{pmatrix}0\\-\dfrac{1}{2}\\-\dfrac{1}{8}\end{pmatrix}= -\dfrac{3}{4}\times 0+0\times \left(-\dfrac{1}{2}\right)+\dfrac{3}{8}\times \left(-\dfrac{1}{8}\right)\not= 0 $$
Le triangle $TPN$ n'est pas rectangle en $T$.

Exercice 4 5 points

Candidats n'ayant pas suivi l'enseignement de spécialité

Un volume constant de 2200 m$^3$ d'eau est réparti entre deux bassins A et B. Le bassin A refroidit une machine. Pour des raisons d'équilibre thermique on crée un courant d'eau entre les deux bassins à l'aide de pompes. On modélise les échanges entre les deux bassins de la façon suivante :

• au départ, le bassin A contient 800~m$^3$ d'eau et le bassin B contient 1400 m$^3$ d'eau ;
• tous les jours, 15 % du volume d'eau présent dans le bassin B au début de la journée est transféré vers le bassin A ;
• tous les jours, 10 % du volume d'eau présent dans le bassin A au début de la journée est transféré vers le bassin B.

  Pour tout entier naturel $n$, on note :

• $a_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin A à la fin du $n$-ième jour de fonctionnement ;
• $b_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin B à la fin du $n$-ième jour de fonctionnement.

 
On a donc $a_{0} = 800$ et $b_{0} = 1400 $.

1. Par quelle relation entre $a_{n}$ et $b_{n}$ traduit-on la conservation du volume total d'eau du circuit ?
2. Justifier que, pour tout entier naturel $n,\: a_{n+1} = \dfrac{3}{4} a_{n} + 330$.
3. L'algorithme ci-dessous permet de déterminer la plus petite valeur de $n$ à partir de laquelle $a_{n}$ est supérieur ou égal à 1100. Recopier cet algorithme en complétant les parties manquantes.
   $$ \begin{array}{|c|c|}\hline\text{ Variables} &n   \text{est un entier naturel} \\ & a   \text{est un nombre réel}\\ \text{Initialisation} & \text{ Affecter à }  n   \text{ la valeur}  0\\ & \text{ Affecter à }  a    \text{  la valeur}  800\\ \text{Traitement} &\text{Tant que}  a <1100   \text{faire}         \\ &\quad\text{Affecter à  }a\text{ la valeur  }\ldots\\ &\quad\text{Affecter à } n \text{ la valeur} \ldots\\ &\text{Fin tant que }\\ \text{Sortie} &\text{Afficher } n \\ \hline \end{array} $$
4. Pour tout entier naturel $n$, on note $u_{n} = a_{n} - 1320$.
   1. Montrer que la suite $\left(u_{n}\right)$ est une suite géométrique dont on précisera le premier terme et la raison.
   2. Exprimer $u_{n}$ en fonction de $n$.
   3. Exprimer $u_{n}$ en fonction de $n$.
      En déduire que, pour tout entier naturel $n,\: a_{n} = 1320 - 520 \times \left(\dfrac{3}{4}\right)^n$.
5.  On cherche à savoir si, un jour donné, les deux bassins peuvent avoir, au mètre cube près, le même volume d'eau. Proposer une méthode pour répondre à ce questionnement.

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Un volume constant de 2200 m$^3$ d'eau est réparti entre deux bassins A et B. Le bassin A refroidit une machine. Pour des raisons d'équilibre thermique on crée un courant d'eau entre les deux bassins à l'aide de pompes. On modélise les échanges entre les deux bassins de la façon suivante :

• au départ, le bassin A contient 800~m$^3$ d'eau et le bassin B contient 1400 m$^3$ d'eau ;
• tous les jours, 15 % du volume d'eau présent dans le bassin B au début de la journée est transféré vers le bassin A ;
• tous les jours, 10 % du volume d'eau présent dans le bassin A au début de la journée est transféré vers le bassin B.

  Pour tout entier naturel $n$, on note :

• $a_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin A à la fin du $n$-ième jour de fonctionnement ;
• $b_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin B à la fin du $n$-ième jour de fonctionnement.

 
On a donc $a_{0} = 800$ et $b_{0} = 1400 $.

1. Par quelle relation entre $a_{n}$ et $b_{n}$ traduit-on la conservation du volume total d'eau du circuit ?

«&nbs;Un volume constant de 2200}~m$^3$ d'eau est réparti entre deux bassins A et B.»  donc $$ \text{Pour tout }n \text{ de } \mathbb{N},\ a_n+b_n = 2200 .$$
2. Justifier que, pour tout entier naturel $n,\: a_{n+1} = \dfrac{3}{4} a_{n} + 330$.

Au début du $n+1$-ième jour, la bassin A contient $a_n$, on ajoute 15 % du volume d'eau présent dans le bassin B soit $ 0,15 b_n $ et on enlève 10 % du volume présent dans A au début de la journée :
$ a_{n+1}= a_n + 0,15 b_n -0,1 a_n = a_n + 0,15 (2200 - a_n)-0,1a_n =0,75a_n+330 =\dfrac{3}{4} a_{n} + 330 $
On a bien, pour tout entier naturel $n,a_{n+1} = \dfrac{3}{4} a_{n} + 330$.
3. L'algorithme ci-dessous permet de déterminer la plus petite valeur de $n$ à partir de laquelle $a_{n}$ est supérieur ou égal à 1100. Recopier cet algorithme en complétant les parties manquantes.
   $$ \begin{array}{|c|c|}\hline\text{ Variables} &n   \text{est un entier naturel} \\ & a   \text{est un nombre réel}\\ \text{Initialisation} & \text{ Affecter à }  n   \text{ la valeur}  0\\ & \text{ Affecter à }  a    \text{  la valeur}  800\\ \text{Traitement} &\text{Tant que}  a <1100   \text{faire}         \\ &\quad\text{Affecter à  }a\text{ la valeur  }\ldots\\ &\quad\text{Affecter à } n \text{ la valeur} \ldots\\ &\text{Fin tant que }\\ \text{Sortie} &\text{Afficher } n \\ \hline \end{array} $$

4. Pour tout entier naturel $n$, on note $u_{n} = a_{n} - 1320$.
   1. Montrer que la suite $\left(u_{n}\right)$ est une suite géométrique dont on précisera le premier terme et la raison.
   
   Remarque : on peut calculer les premiers termes pour avoir la raison. Pour tout entier naturel $n$, on a $ \begin{array}{lll} u_{n+1} &= a_{n+1} - 1320 & \text{définition de } u_n \\[5pt] &=\dfrac{3}{4} a_{n} + 330 - 1320 & \text{question 2. } \\[8pt] &= \dfrac{3}{4} a_{n} -990 & \\[8pt] & = \dfrac{3}{4}\left( a_{n} - 1320\right) & \\[8pt] & = \dfrac{3}{4} u_{n} & \text{définition de } u_n \\[8pt] \end{array} $
   On reconnait la définition d'une suite géométrique de raison $ \dfrac{3}{4} $. Son premier terme est $ u_0 = a_0 -1320 = 800-1320 = -520 $
   2. Exprimer $u_{n}$ en fonction de $n$.
      En déduire que, pour tout entier naturel $n,\: a_{n} = 1320 - 520 \times \left(\dfrac{3}{4}\right)^n$.
   
   On a donc, pour tout entier naturel $n$, $u_{n} = u_0 q^n = -520\times \left(\dfrac{3}{4} \right)^n$ . Mais, par définition de $u_n$, on a $u_{n} = a_{n} - 1320 \Leftrightarrow a_n = u_n + 1320$ donc $a_{n} = 1320 - 520 \times \left(\dfrac{3}{4}\right)^n$.
5.  On cherche à savoir si, un jour donné, les deux bassins peuvent avoir, au mètre cube près, le même volume d'eau. Proposer une méthode pour répondre à ce questionnement.

On cherche à savoir si, un jour donné, les deux bassins peuvent avoir, au mètre cube près, le même volume d'eau.
Si ce jour arrive, on aura $ a_n = b_n = \dfrac{2200}{2}=1100$.
Il faut donc résoudre l'équation $ 1320 - 520 \times \left(\dfrac{3}{4}\right)^n = 1100 $ d'inconnue $n$. $ 1320 - 520 \times \left(\dfrac{3}{4}\right)^n = 1100 \Leftrightarrow 520 \times \left(\dfrac{3}{4}\right)^n = 220 \Leftrightarrow \left(\dfrac{3}{4}\right)^n = \dfrac{11}{26} \Leftrightarrow n \ln \left( \dfrac{3}{4} \right) = \ln \left( \dfrac{11}{26} \right)$ Finalement $ n = \dfrac{\ln \left( \dfrac{11}{26} \right)}{\ln \left( \dfrac{3}{4} \right) } \approx 2,99$ .
On vérifie: $ a_3 = 1100,625 $ et $ b_3 = 1099,375 $ donc $ a_3 - b_3 =1,25 > 1 $.
A la fin du troisième jour, les deux bassins auront le même volume au mètre cube près. Les deux bassins n'auront donc jamais le même volume d'eau, à un mètre cube près.

Spécialité 5 points

Candidats ayant suivi l'enseignement de spécialité
Un volume constant de 2200  m$^3$ d'eau est réparti entre deux bassins A et B. Le bassin A refroidit une machine. Pour des raisons d'équilibre thermique on crée un courant d'eau entre les deux bassins à l'aide de deux pompes. On modélise les échanges entre les deux bassins de la façon suivante :

• au départ, le bassin A contient 1100 m$^3$ d'eau et le bassin B contient 1100 m$^3$ d'eau ;
• tous les jours, 15 % du volume d'eau présent en début de journée dans le bassin B est transféré vers le bassin A ;
• tous les jours, 10 % du volume d'eau présent en début de journée dans le bassin du bassin A est transféré vers le bassin B, et pour des raisons de maintenance, on transfère également 5~m$^3$ du bassin A vers le bassin B.

Pour tout entier naturel $n$, on note :

• $a_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin A à la fin du $n$-ième jour de fonctionnement ;
• $b_{n}$ le volume d'eau, exprimé en m$^3$, contenu dans le bassin B à la fin du $n$-ième jour de fonctionnement.

  On a donc $a_{0} = 1100$ et $b_{0} = 1100$. Les parties A et B peuvent être traitées de manière indépendante
Partie A

1. Traduire la conservation du volume total d'eau du circuit par une relation liant $a_{n}$ et $b_{n}$.
2. On utilise un tableur pour visualiser l'évolution du volume d'eau dans les bassins.
Donner les formules à écrire et à recopier vers le bas dans les cellules B3 et C3 permettant d'obtenir la feuille de calcul ci-dessous : $$\begin{array}{|c|c|c|c|} \hline & A & B & C \\ \hline 1& \text{Jour}  n & \text{Volume bassin }  A & \text{Volume bassin}  B\\ \hline 2 & 0 & 1100,00 & 1100,00\\ \hline 3 &1 & &\\ \hline 4 & 2 & 1187,50 & 1012,50\\ \hline 5 & 3 &1215,63 &984,38\\ \hline 6 &4 &1236,72 &963,28\\ \hline 7 &5 &1252,54 &947,46\\ \hline 8 & 6 &1264,40 &935,60\\ \hline 9 &7 &1273,30 &926,10 \\ \hline 10 &8 &1279,98 &920,02 \\ \hline 11 &9 &1234,98 &915,02\\ \hline 12 &10 &1288,74 &911,26\\ \hline 13 &11 &1291,55 &908,45\\ \hline 14 &12 &1293,66 &906,34\\ \hline 15 &13 &1295,25 &904,75\\ \hline 16 &14 &1296,44 &903,56\\ \hline 17 &15 &1297,33 &902,67\\ \hline 18 &16 &1298,00 &902,00\\ \hline 19 &17 &1298,50 &901,50\\ \hline 20 &18 &1298,87 &901,13\\ \hline \end{array}$$
3. Quelles conjectures peut-on faire sur l'évolution du volume d'eau dans chacun des bassins ?

Partie B
  On considère la matrice carrée $M = \begin{pmatrix}0,9& 0,15\\0,1&0,85 \end{pmatrix}$ et les matrices colonnes $R = \begin{pmatrix}-5\\5 \end{pmatrix}$ et $X_{n} = \begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$.

On admet que, pour tout entier naturel $n,\: X_{n+1} = M X_{n} + R$.

1. On note $S = \begin{pmatrix} 1300\\ 900\end{pmatrix}$. Vérifier que $S = MS + R$.
En déduire que, pour tout entier naturel $n,\: X_{n+1} - S = M\left(X_{n} - S\right)$.
  Dans la suite, on admettra que, pour tout entier naturel $n,\: X_{n} - S = M^n\left(X_{0} - S\right)$ et que $M^n = \begin{pmatrix} 0,6 + 0,4 \times 0,75^n& 0,6 - 0,6 \times 0,75^n\\ 0,4 - 0,4 \times 0,75^n& 0,4 + 0,6 \times 0,75^n \end{pmatrix}$.

2. Montrer que, pour tout entier naturel $n,\: X_{n} = \begin{pmatrix}1300 - 200 \times 0,75^n\\900 + 200 \times 0,75^n \end{pmatrix}$.
3. Valider ou invalider les conjectures effectuées à la question 3. de la partie A.
4. On considère que le processus est stabilisé lorsque l'entier naturel $n$ vérifie
   \[1300- a_{n} < 1,5\quad \text{et} \quad b_{n} - 900 < 1,5.\] Déterminer le premier jour pour lequel le processus est stabilisé.

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

  On a donc $a_{0} = 1100$ et $b_{0} = 1100$. Les parties A et B peuvent être traitées de manière indépendante
Partie A

1. Traduire la conservation du volume total d'eau du circuit par une relation liant $a_{n}$ et $b_{n}$.

La conservation du volume total se traduit par: pour tout entier naturel $n$, $a_n+b_n=2200 $.
2. On utilise un tableur pour visualiser l'évolution du volume d'eau dans les bassins.Donner les formules à écrire et à recopier vers le bas dans les cellules B3 et C3 permettant d'obtenir la feuille de calcul ci-dessous : $$\begin{array}{|c|c|c|c|} \hline & A & B & C \\ \hline 1& \text{Jour}  n & \text{Volume bassin }  A & \text{Volume bassin}  B\\ \hline 2 & 0 & 1100,00 & 1100,00\\ \hline 3 &1 & &\\ \hline 4 & 2 & 1187,50 & 1012,50\\ \hline 5 & 3 &1215,63 &984,38\\ \hline 6 &4 &1236,72 &963,28\\ \hline 7 &5 &1252,54 &947,46\\ \hline 8 & 6 &1264,40 &935,60\\ \hline 9 &7 &1273,30 &926,10 \\ \hline 10 &8 &1279,98 &920,02 \\ \hline 11 &9 &1234,98 &915,02\\ \hline 12 &10 &1288,74 &911,26\\ \hline 13 &11 &1291,55 &908,45\\ \hline 14 &12 &1293,66 &906,34\\ \hline 15 &13 &1295,25 &904,75\\ \hline 16 &14 &1296,44 &903,56\\ \hline 17 &15 &1297,33 &902,67\\ \hline 18 &16 &1298,00 &902,00\\ \hline 19 &17 &1298,50 &901,50\\ \hline 20 &18 &1298,87 &901,13\\ \hline \end{array}$$

D'après le texte, on peut dire que: $\left\lbrace \begin{array}{ l l} a_{n+1} =& 0,9 a_n + 0,15 b_n - 5\\ b_{n+1}= & 0,1a_n + 0,85b_n + 5 \end{array} \right.$ avec $\left\lbrace \begin{array}{ l l} a_{0}= & 1100\\ b_{0} =& 1100 \end{array} \right.$
On utilise un tableur pour visualiser l'évolution du volume d'eau dans les bassins. On donne les formules à écrire et à recopier vers le bas dans les cellules B3 et C3 permettant d'obtenir la feuille de calcul du texte:


3. Quelles conjectures peut-on faire sur l'évolution du volume d'eau dans chacun des bassins ?

La suite $(a_n)$ donnant le volume d'eau dans le bassin A semble croissante et tendre vers 1300 , tandis que la suite $(b_n)$ donnant le volume d'eau dans le bassin B semble décroissante et tendre vers 900.

Partie B

1. On note $S = \begin{pmatrix} 1300\\ 900\end{pmatrix}$. Vérifier que $S = MS + R$.En déduire que, pour tout entier naturel $n,\: X_{n+1} - S = M\left(X_{n} - S\right)$.
     Dans la suite, on admettra que, pour tout entier naturel $n,\: X_{n} - S = M^n\left(X_{0} - S\right)$ et que $M^n = \begin{pmatrix} 0,6 + 0,4 \times 0,75^n& 0,6 - 0,6 \times 0,75^n\\ 0,4 - 0,4 \times 0,75^n& 0,4 + 0,6 \times 0,75^n \end{pmatrix}$.
$MS = \begin{pmatrix}0,9& 0,15\\0,1&0,85 \end{pmatrix} \times \begin{pmatrix} 1300\\ 900\end{pmatrix} = \begin{pmatrix} 0,9\times 1300+ 0,15\times 900\\ 0,1\times 1300+ 0,85\times 900 \end{pmatrix} = \begin{pmatrix} 1305\\ 895\end{pmatrix}$ $MS+R = \begin{pmatrix} 1305\\ 895\end{pmatrix} + \begin{pmatrix} -5\\ 5\end{pmatrix} = \begin{pmatrix} 1300\\ 900\end{pmatrix} =S$
On a $X_{n+1}=MX_{n}+ R$ et $S=MS+R$; par soustraction membre à membre, on obtient: $X_{n+1}-S = MX_{n}+R -MS - R = MX_{n}-MS = M(X_{n}-S)$
2. Montrer que, pour tout entier naturel $n,\: X_{n} = \begin{pmatrix}1300 - 200 \times 0,75^n\\900 + 200 \times 0,75^n \end{pmatrix}$.
$X_0=\begin{pmatrix} 1100\\1100\end{pmatrix}$ et $ S=\begin{pmatrix} 1300\\900\end{pmatrix}$ donc $X_0 - S =\begin{pmatrix} -200 \\ 200 \end{pmatrix}$ $M^n\times (X_0 - S) = \begin{pmatrix} 0,6 + 0,4 \times 0,75^n& 0,6 - 0,6 \times 0,75^n\\ 0,4 - 0,4 \times 0,75^n& 0,4 + 0,6 \times 0,75^n \end{pmatrix} \times \begin{pmatrix} -200 \\ 200 \end{pmatrix}$ $\phantom{M^n\times (X_0 - S)} = \begin{pmatrix} (0,6 + 0,4 \times 0,75^n)\times(-200) + (0,6 - 0,6 \times 0,75^n)\times 200 \\ (0,4 - 0,4 \times 0,75^n)\times (-200) + (0,4 + 0,6 \times 0,75^n)\times 200 \end{pmatrix} = \begin{pmatrix} -200\times 0,75^{n} \\ 200\times 0,75^{n} \end{pmatrix}$ Donc $X_{n}=M^n\times (X_0 - S) +S = \begin{pmatrix} -200\times 0,75^{n} \\ 200\times 0,75^{n} \end{pmatrix} + \begin{pmatrix} 1320\\ 900 \end{pmatrix} = \begin{pmatrix} 1320-200\times 0,75^{n} \\ 900+200\times 0,75^{n} \end{pmatrix}$
3. Valider ou invalider les conjectures effectuées à la question 3. de la partie A.

$X_{n}= \begin{pmatrix} 1320-200\times 0,75^{n} \\ 900+200\times 0,75^{n} \end{pmatrix}$ et $X_{n}= \begin{pmatrix} a_n\\ b_n \end{pmatrix}$ donc $\left\lbrace \begin{array}{@ l @{\ =\ } l} a_{n} & 1300 - 200 \times 0,75^{n}\\ b_{n} & 900 + 200 \times 0,75^{n} \end{array} \right.$ La suite $(0,75^n)$ est géométrique de raison $0,75$ donc est décroissante; on multiplie par un nombre négatif, donc la suite $(-200\times 0,75^n)$ est croissante et donc la suite $(a_n)$ est croissante. De plus, $-1 < 0,75 < 1$ donc la suite $(0,75^n)$ est convergente et a pour limite 0. On peut en déduire que la suite $(a_n)$ est convergente et a pour limite $1320$. Pour les mêmes raisons, on peut dire que la suite $(b_n)$ est décroissante, et convergente vers 900.
4. On considère que le processus est stabilisé lorsque l'entier naturel $n$ vérifie
   \[1300- a_{n} < 1,5\quad \text{et} \quad b_{n} - 900 < 1,5.\] Déterminer le premier jour pour lequel le processus est stabilisé.

D'après le tableau fourni dans le texte, la plus petite valeur de $n$ pour que le processus soit stabilisé peut être 17 ou 18. Pour $n=17$, $a_{17} \approx 1298,4966$ donc $1300- a_{17} > 1,5$. Pour $n=18$, $a_{18} \approx 1298,8724$ donc $1300- a_{18} < 1,5$. Comme $a_n + b_n = 2200$, $b_n=2200-a_n$ ce qui équivaut à $b_n -900 = 1300 - a_n$; donc $1300-a_n < 1,5 \iff b_n-900 <1,5$. On peut donc dire que le processus est stabilisé à partir de $n=18$.

Annexe Exercice 2

Annexe Exercice 3