Baccalauréat STI2D et STL spécialité SPCLMétropole -- 7 septembre 2017 - Correction Exercice 3

Page 6 sur 8: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Nombres complexes et loi exponentielle

Les partie A et B sont indépendantes.

Partie A

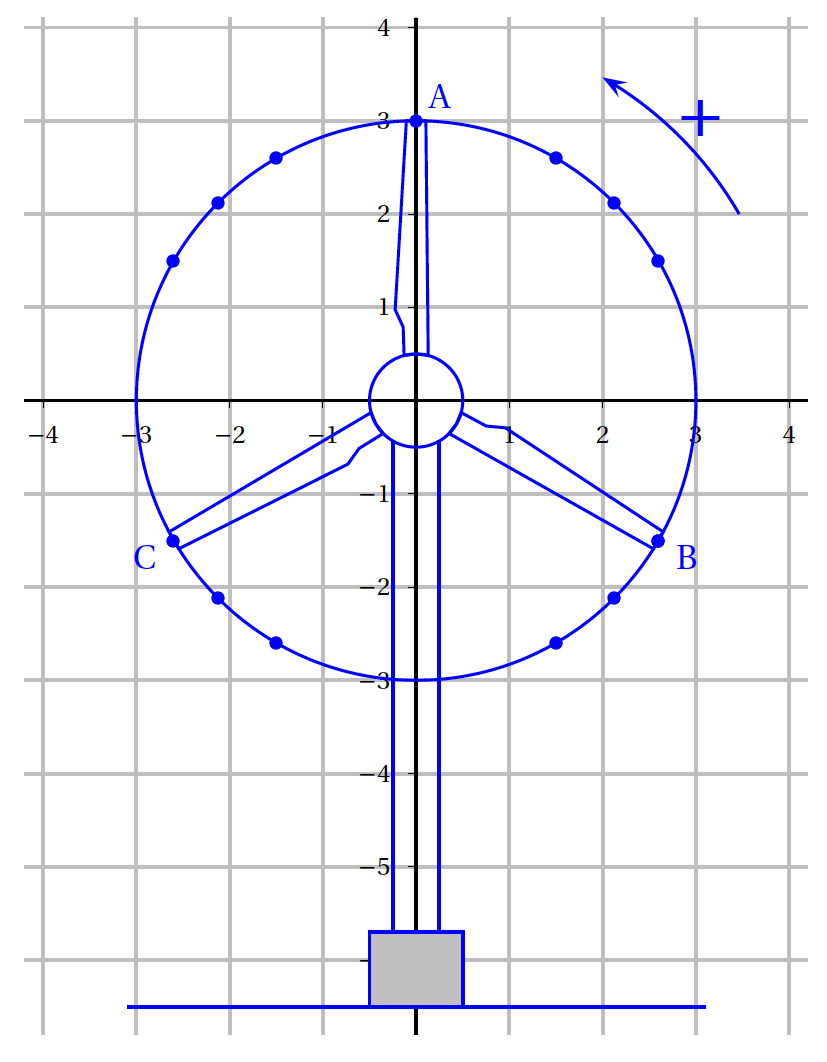
Dans le plan complexe muni d'une repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$, on représente les extrémités des pales d'une éolienne par le point A de coordonnées $(0~;~3)$ et par les points B et C d'affixes respectives:
$z_{\text B} = \dfrac{3\sqrt{3}}{2} - \dfrac{3}{2}\text{i}$ et $z_{\text C} = 3\text{e}^{-\text{i}\frac{5\pi}{6}}$.

1. Soit $z_{\text A}$ l'affixe du point A.
   1. Donner la forme algébrique de $z_{\text A}$.
   La forme algébrique de $z_A$ est $z_A=3⁢i$.
   2. Donner la forme exponentielle de $z_{\text A}$.
   La forme exponentielle de $z_A$ est $z_A=3⁢\text{e}^{\text{i}\frac{\pi}{2}}$.
2. Déterminer la forme exponentielle de $z_{\text B}$.
$z_{\text B} = \dfrac{3\sqrt{3}}{2} - \dfrac{3}{2}\text{i}$ $$\begin{array}{cc} \text{Module}& \text{Argument}\\ \begin{array}{rl|rl} |z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ \left( \dfrac{3\sqrt{3}}{2} \right) ^2+\left( - \dfrac{3}{2}\right) ^2}\\ &=\sqrt {\dfrac{27}{4} +\dfrac{9}{4}}\\ &= =\sqrt {\dfrac{36}{4} }=\sqrt 9\\ &=3 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\dfrac{a}{r}~=\dfrac{ \dfrac{3\sqrt{3}}{2} }{3}=\frac{\sqrt 3}{2} \\ ~\sin \theta=\dfrac{b}{r}~=-\dfrac{\dfrac{3}{2}}{3}= -\dfrac{1}{2} \end{array} \right.\\ &\text{ Donc } \theta = -\frac{\pi}{6} \text{ convient } \end{array}$$ $$z_{\text B} = \dfrac{3\sqrt{3}}{2} - \dfrac{3}{2}\text{i}= 3\left(\cos\left(-\frac{\pi}{6} \right) +i\sin \left(-\frac{\pi}{6} \right) \right) $$ La forme exponentielle de $z_B$ est $z_A=3⁢\text{e}^{-\text{i}\frac{\pi}{6}}$.
3. On admet que lorsque l'hélice tourne d'un angle de $\dfrac{\pi}{2}$ radians dans le sens direct, les points A, B et C sont transformés respectivement en A$'$, B$'$ et C$'$ tels que:
   • A$'$ a pour affixe $z_{\text{A}'} = z_{\text A}\times\text{e}^{\text{i}\frac{\pi}{2}}$
   • B$'$ a pour affixe $z_{\text{B}'} = z_{\text B}\times\text{e}^{\text{i}\frac{\pi}{2}}$
   • C$'$ a pour affixe $z_{\text{C}'} = z_{\text C}\times\text{e}^{\text{i}\frac{\pi}{2}}$
   Déterminer la forme exponentielle de $z_{\text{C}'}$;
$$\begin{array}{rl} z_C'&=z_{\text C}\times\text{e}^{\text{i}\frac{\pi}{2}} \\ & = 3\text{e}^{-\text{i}\frac{5\pi}{6}}\times \text{e}^{\text{i}\frac{\pi}{2}} \\ &= 3 \text{e}^{-\text{i}\left(\frac{5\pi}{6}+\frac{\pi}{2}\right) }\\ &= 3 \text{e}^{-\text{i}\left(\frac{5\pi}{6}+\frac{3\pi}{6}\right) }\\ &= 3 \text{e}^{-\text{i}\frac{2\pi}{6} }\\ &= 3 \text{e}^{-\text{i}\frac{\pi}{3} }\\ \end{array}$$ La forme exponentielle de $z_C'$ est $z_C'=3⁢\text{e}^{-\text{i}\frac{\pi}{3}}$.

Partie B

La durée de vie, en jours, d'un des composants électroniques d'une éolienne est modélisée par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda=0,002$.

1. Calculer la durée de vie moyenne, en jours, d'un composant de ce type.
L'espérance mathématique de la variable aléatoire $T$ suivant la loi exponentielle de paramètre $\lambda =0,002$ est : $$E(T)=\dfrac{1}{\lambda}=\dfrac{1}{ 0,002}=500$$ La durée de vie moyenne d'un composant est de 500 jours.
2. 1. On considère la fonction $f$ définie sur $[0~;~+\infty[$ par $f(x)=0,002\text{e}^{-0,002x}$. 
      Montrer que la fonction $F$ définie sur l'intervalle $[0~;~+\infty[$ par $F(x)=-\text{e}^{-0,002x}$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~+\infty[$.
   Pour tout réel $x$ positif, posons $u⁡(x)=-0,002⁢x$, d'où $u′⁡(x)=-0,002$.
   Par conséquent, sur l'intervalle $[0~;~+\infty[$, $$\begin{array}{rl} F'(x)& =-u′⁡(x)\times \text{e}^{u(x)}\\ & =-\left(-0,002\text{e}^{-0,002x}\right)\\ &= 0,002\text{e}^{-0,002x}\\ &= f(x) \end{array}$$ Ainsi, une primitive de la fonction $f$ est la fonction $F$ définie sur l'intervalle $[0~;~+\infty[$ par $F(x)=-\text{e}^{-0,002x}$.
   2. On rappelle que, pour tout nombre réel de $[0~;~+\infty[$, $P(T\leq t)=\displaystyle\int_{0}^{t} f(x) d x$. On a donc $P(T\leq t) = 1 -\text{e}^{-0,002 t}$. Le fabricant affirme: « la probabilité que la durée de vie du composant soit supérieure à 100 jours est d'au moins $0,8$. » Que penser de cette affirmation? Justifier la réponse.
   La probabilité que la durée de vie du composant soit supérieure à 100 jours est $P(T>100)=1-P(T\leq 100)$ soit : $$\begin{array}{rl} P(T>100)&= 1-\left( 1- \text{e}^{-0,002\times 100}\right)\\ &= \text{e}^{-0,2}\\ &\approx 0,819 \end{array}$$ La probabilité que la durée de vie du composant soit supérieure à 100 jours est supérieure à 0,8 donc le fabricant a raison.