Baccalauréat STI2D et STL spécialité SPCLMétropole -- 7 septembre 2017 - Correction Exercice 2

Page 4 sur 8: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Equations différentielles et exponentielles

Le stimulateur cardiaque est un appareil destiné à certaines personnes dont le rythme du coeur est devenu trop lent. Implanté sous la peau, l'appareil envoie des impulsions électriques régulières au coeur lorsque le rythme cardiaque est insuffisant.

Un stimulateur cardiaque est constitué de deux composants:
• un condensateur de capacité $C$ égale à $4\times 10^{-7}$ farad;
• un conducteur ohmique de résistance $R$ égale à $2\times 10^{6}$ ohms.

Une fois le condensateur chargé, la tension à ses bornes est égale à 5,6 volts. Il se décharge ensuite dans le conducteur ohmique.

Partie A

La tension $u$, en volts, aux bornes du condensateur est une fonction du temps $t$, en secondes. On admet que $u(0)=5,6$ et que cette fonction $u$, définie et dérivable sur l'intervalle $[0~;~+\infty[$, vérifie pour tout nombre $t$ de l'intervalle $[0~;~+\infty[$ la relation: $$u'(t) + \dfrac{1}{RC} \times u(t)=0$$ où $u'$ désigne la fonction dérivée de la fonction $u$.

1. 1. Vérifier que la fonction $u$ est solution sur l'intervalle $[0~;~+\infty[$ de l'équation différentielle $y'+1,25y=0$.
   Avec $R=2\times 10^6$ et $C=4\times 10^{-7}$ on a, pour tout réel $t $ de l'intervalle $[0~;~+\infty[$ : $$\begin{array}{rl} u'(t) + \dfrac{1}{RC} \times u(t)=0&\iff u’(t)+ \dfrac{1}{2\times 10^{6}\times 4\times 10^{-7}} \times u(t)=0 \\ &\iff u’(t)+ 1,25\times u(t)=0 \\ \end{array}$$ Ainsi, la fonction $u$ est solution sur l'intervalle $[0~;~+\infty[$ de l'équation différentielle $y’+1,25⁢y=0.$
   2. Résoudre l'équation différentielle $y'+1,25y=0$.
   On met l''équation sous forme résolue : $y'=ay$.
   $y'+1,25y=0\iff y'=-1,25 y$
   Les solutions de l'équation différentielle : $y′+1,25⁢y=0 $ sont les fonctions $u$ définies par $u(t)=k⁢\text{e}^{-1,25⁢t}$ où $k$ est un réel .
   3. Montrer que pour tout nombre réel $t$ de l'intervalle $[0~;~+\infty[$, on a: $u(t)=5,6\text{e}^{-1,25t}$.
   $u(t)=k⁢\text{e}^{-1,25⁢t}$ et $u(0)=5,6$ d'où $k⁢\text{e}^{0}=5,6$ soit $k=5,6$.
   
   La fonction $u$ est définie pour tout réel $t$ de l'intervalle $[0~;~+\infty[$ par $u(t)=5,6⁢\text{e}^{-1,25⁢t}$.
2. 1. Etudier mathématiquement le sens de variation de la fonction $u$ sur l'intervalle $[0~;~+\infty[$.
   Les variations de la fonction $u$ se déduisent du signe de sa dérivée. Pour tout réel $t $ de l'intervalle $[0~;~+\infty[$ :
   $u’(t)=5,6⁢\times(-1,25)\text{e}^{-1,25⁢t}=\text{e}^{-1,25⁢t}$
   Comme pour tout réel $t, \text{e}^{-1,25⁢t}>0$ on en déduit que sur l'intervalle $[0~;~+\infty[$, $u′⁡(t)<0$.
   La fonction $u$ est strictement décroissante sur l'intervalle $[0~;~+\infty[$.
   2. Ce résultat était-il prévisible. Justifier la réponse.
   Comme le condensateur se décharge dans le conducteur ohmique, la tension aux bornes du condensateur diminue avec le temps.

Partie B

En réalité, lorsque la tension $u$ aux bornes du condensateur a perdu 63 % de sa valeur initiale $u(0)$, le stimulateur cardiaque envoie une impulsion électrique au coeur, ce qui provoque un battement. On considère que le condensateur se recharge instantanément et que la tension mesurée à ses bornes est à nouveau égale à 5,6 volts.

 

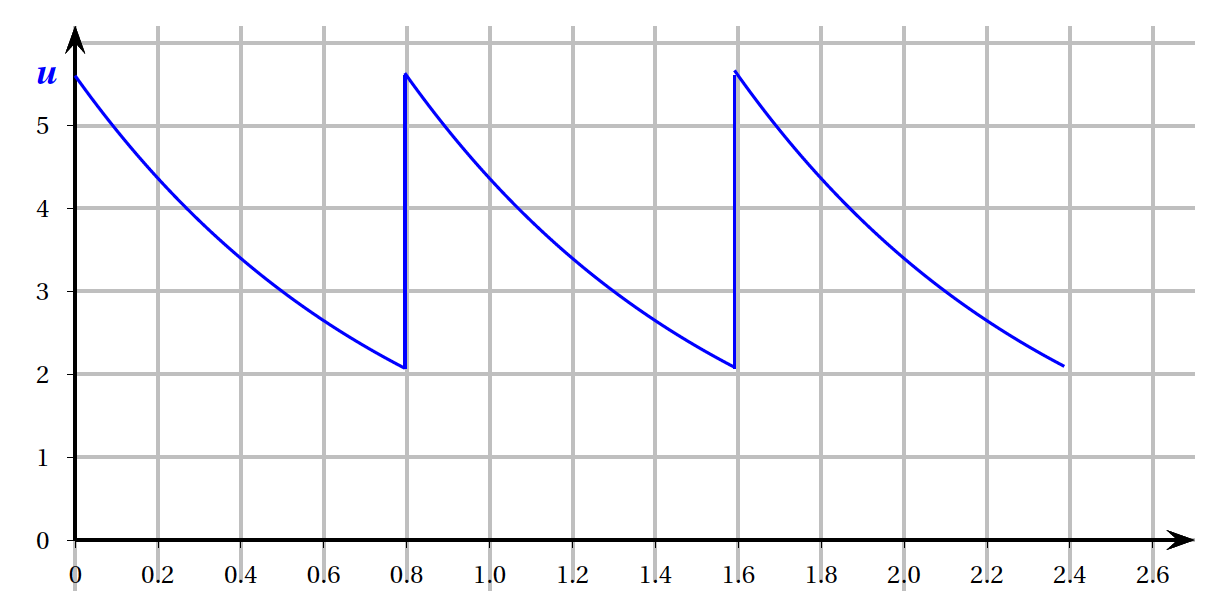
1. 1. Vérifier que la tension aux bornes du condensateur qui déclenche l'envoi d'une impulsion électrique au coeur est de 2,072 volts.
   La tension aux bornes après une perte de 63 % de sa valeur initiale est : $$5,6\times \left( 1-\frac{63}{100}\right) =2,072$$
   La tension aux bornes du condensateur qui déclenche l'envoi d'une impulsion électrique au cœur est de 2,072 volts.
   2. Résoudre dans l'intervalle $[0~;~+\infty[$ l'équation: $$5,6\text{e}^{-1,25t} = 2,072.$$
   $$\begin{array}{rl} 5,6\text{e}^{-1,25t} = 2,072 & \iff \text{e}^{-1,25t} = \dfrac{2,072}{5,6r}\\ & \iff \text{e}^{-1,25t} = 0,37\\ & \iff \ln \left( \text{e}^{-1,25t}\right) = \ln(0,37)\\ &\iff -1,25 t= \ln(0,37)\\ &\iff t= -\dfrac{\ln(0,37)}{1,25}\\ &\iff t= -0,8\ln(0,37) \end{array}$$
   L'équation: $5,6\text{e}^{-1,25t} = 2,072 $ a pour solution $t= -0,8\ln(0,37)$.
   3. Interpréter le résultat trouvé.
   $$t= -0,8\ln(0,37)\approx 0,8$$
   Le stimulateur cardiaque envoie une impulsion électrique au cœur toutes les 0,8 secondes.
2. Chez l'adulte en bonne santé, le pouls au repos se situe entre 50 et 80 pulsations par minute.
   On admet que le stimulateur cardiaque d'un patient souffrant d'insuffisance envoie une impulsion électrique au coeur toutes les 0,8 secondes.
   Ce rythme correspond-il à celui d'un adulte au repos et en bonne santé? Justifier la réponse.
Le nombre de pulsations par minute est : $\dfrac{60}{0,8}=75$
Le nombre de pulsations par minute correspond au rythme d'un adulte en bonne santé.