BAC STL, STI2D Métropole 16 juin 2017 - Correction Exercice 4
Page 8 sur 8
Exercice 4 4 points
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie. Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l’évaluation.
Une réponse non justifiée ne rapporte aucun point.
- Proposition 1 : Le nombre complexe $z$ de module $4\sqrt 3$ et dont un argument est$\frac{2\pi}{3}$ a pour forme algébrique $-2\sqrt 3 + 6i$. Le nombre complexe $z$ de module $4\sqrt 3$ et dont un argument est$\frac{2\pi}{3}$ a pour forme algébrique $-2\sqrt 3 + 6i$.\\ Le nombre complexe $z$ de module $4\sqrt 3$ et dont un argument est$\frac{2\pi}{3}$ s'écrit : $$\begin{array}{rl} z &=4\sqrt 3 \text{e}^{i \frac{2\pi}{3}} \\ &= 4\sqrt 3 \left( \cos \left( \frac{2\pi}{3}\right) +i \sin \left( \frac{2\pi}{3}\right) \right) \\ &= 4\sqrt 3 \left( -\frac{1}{2}+i \frac{\sqrt 3}{2} \right) \\ &= 4\sqrt 3 \times \left( -\frac{1}{2}\right) + 4\sqrt 3 \times \frac{\sqrt 3}{2}\\ &= -2\sqrt 3 + 6i \end{array}$$
- Le plan est muni d’un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Les points A, B et C ont pour affixes respectives $z_A=2\text{e}^{i\frac{\pi}{2}} , z_B = -1 + i\sqrt 3$ et $z_C = z_A\times z_B$.
Proposition 2 : Le point $C$ appartient au cercle de centre O et de rayon 4. On peut par exemple calculer $z_C$ sous forme algébrique puis calculer son module. $$\begin{array}{rl} z_A=2\text{e}^{i\frac{\pi}{2}}&= 2 \left( \cos \left( \frac{\pi}{2}\right) +i \sin \left( \frac{\pi}{2}\right) \right) \\ & = 2( 0 + i)\\ &= 2i \end{array}$$ On a alors : $$\begin{array}{rl} z_C = z_A\times z_B& = 2i \times \left( -1 + i\sqrt 3\right) \\ & = -2i +2 i^2\sqrt 3\\ &= -2\sqrt 3 -2i \end{array}$$ On déduit alors : $$\begin{array}{rl} OC = |z_C |&=\sqrt{a^2+b^2} \\ & =\sqrt{ (2\sqrt 3)^2+2^2}\\ &=\sqrt{ 12+4}=\sqrt{16}\\ &= 4 \\ \end{array}$$ $OC=4$; donc le point $C$ appartient au cercle de centre O et de rayon 4. - On a tracé ci-dessous dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j}\right)$ la courbe représentative de la fonction $f$ définie sur l’intervalle [0 ; 2] par $f(x) = -\frac{1}{2}x+ 1$.
On considère un point M de coordonnées $ \left( x, -\frac{1}{2}x+ 1\right) $ sur la courbe $\mathcal{C}$, ainsi que les points $H(x,0)$ et $K(0,-\frac{1}{2}x+ 1)$.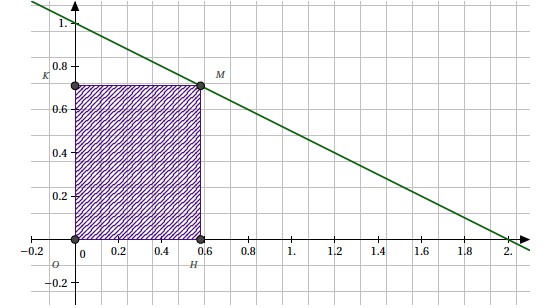
Proposition 3 : L'aire, en unités d’aire, du rectangle $OHMK$ est maximale lorsque $M$ a pour abscisse 1. L'aire du rectangle $OHMK$ est lafonction $g$ définie sur $g$ définie sur $[0;2]$ par $ g(x)= OH\times OK$. - On peut modéliser le temps d’attente d’un client, en minutes, à la caisse d’un supermarché par une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$.
Des études statistiques montrent que la probabilité qu’un client attende plus de 7 minutes à cette caisse est 0,417.
On rappelle que pour tout réel $t$ positif, $P(T> t) =\text{e}^{-\lambda t}$.
Proposition 4 : Le temps moyen d’attente à cette caisse de supermarché est 9 minutes. D'après l'énoncé $P(T> 7) =0,417$. $$\begin{array}{rl} P(T> 7) =0,417 & \iff \text{e}^{-7\lambda} =0,417\\ &\iff \ln \left( \text{e}^{-7\lambda}\right) =\ln(0,417)\\ &\iff -7 \lambda =\ln(0,417) \\ &\iff \lambda = -\dfrac{ \ln(0,417)}{7} \end{array}$$ Le temps d'attente moyen à ce supermarché est $E(T)= \dfrac{1}{\lambda }= -\dfrac{7}{ \ln(0,417)}\approx 8,003$
La proposition 1 est donc vraie.
La proposition 2 est donc vraie.
Or $OH= x$ et $OK= -\frac{1}{2}x+ 1$.
On a donc $g(x)= x\left( -\frac{1}{2}x+ 1\right) =-\frac{1}{2}x^2+ x$.
Calculons sa dérivée :
$g'(x)= -\frac{1}{2}\times 2x+1 =-x+1$
Etudions le signe de la dérivée :
$g'(x)> 0 \iff 1-x> 0 \iff -x> -1\iff x<1$ On déduit le tableau de variations de $g$ sur $[0;2]$:
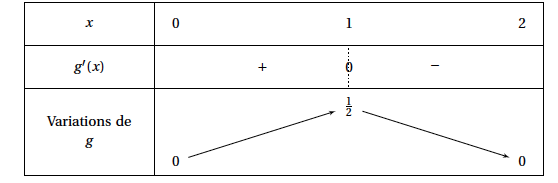
Ainsi l'aire, en unités d’aire, du rectangle $OHMK$ est maximale lorsque $M$ a pour abscisse 1.
La proposition 3 est donc vraie.
Le temps d'attente moyen à ce supermarché est envion 8 miutes.
La proposition 4 est donc fausse.
- Vues: 22983
