Bac STI2D Antilles Guyane 22 juin 2015 - Exercice 5

Page 9 sur 10: Exercice 5

Exercice 5 4 points

Equations différentielles

On étudie la charge d'un condensateur et l'on dispose pour cela du circuit électrique ci-contre composé de :

• une source de tension continue $E$ de 10 V.
• une résistance $R$ de $10^5$\: $\Omega$.
• un condensateur de capacité $C$ de $10^{-6}$ F.

On note $u$ la tension exprimée en volt aux bornes du condensateur. Cette tension $u$ est une fonction du temps $t$ exprimé en seconde. La fonction $u$ est définie et dérivable sur $[0~;~+oo[$ ; elle vérifie l'équation différentielle suivante : \[RCu' + u = E\] où $u'$ est la fonction dérivée de $u$.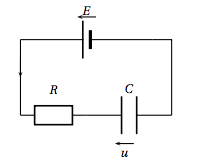

1. Justifier que l'équation différentielle est équivalente à : \[u' + 10u = 100\]
2. 1. Déterminer la forme générale $u(t)$ des solutions de cette équation différentielle.
   2. On considère qu'à l'instant $t = 0$, le condensateur est déchargé. Parmi les solutions, déterminer l'unique fonction $u$ tel que $u(0) = 0$.
   3. Déterminer en justifiant la réponse, la limite en $+ \infty$ de la fonction $u$ ainsi obtenue. En donner une interprétation.
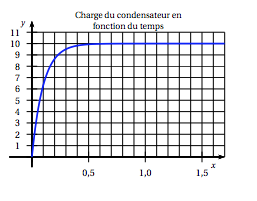
3. On donne ci-dessous la représentation graphique de la fonction $u$ qui vient d'être obtenue à la question 2. b. avec les unités suivantes : 1 unité pour 1 seconde sur l'axe des abscisses et 1 unité pour 1 volt sur l'axe des ordonnées. On appelle $T$ le temps de charge en seconde pour que $u(T)$ soit égal à $95$% de $E$.
   1. Déterminer graphiquement le temps de charge $T$.
   2. Retrouver, par le calcul, le résultat précédent.
   
   
4. Sans modifier les valeurs respectives de $E$ et de $C$, déterminer la valeur de $R$ afin que le temps de charge $T$ soit multiplié par $2$.