Bac STI2D Antilles Guyane 22 juin 2015
Exercice 1 3 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.
Dans cet exercice, i désigne le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$.
- Le temps d'attente en minute à un péage est une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 0,2$ (exprimé en min$^{-1}$). En moyenne une personne attend à ce péage :
- 2 min
- 5 min
- 10 min
- 20 min
- La forme exponentielle du nombre complexe $z = - 3 + \text{i}3\sqrt{3}$ est :
- $3\text{e}^{\text{i}\frac{2\pi}{3}}$
- $6\text{e}^{\text{i}\frac{2\pi}{3}}$
- $6\text{e}^{-\text{i}\frac{2\pi}{3}}$
- $- 6\text{e}^{-\text{i}\frac{2\pi}{3}}$
- On considère le complexe $z = \sqrt{2} - \text{i}\sqrt{2}$. Le nombre complexe $z^2$ est égal à :
- $z^2 = 2$
- $z^2 = 4$
- $z^2 =- 4$
- $z^2 = - 4\text{i}$
Correction de l'exercice 1 (3 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.
Dans cet exercice, i désigne le nombre complexe de module 1 et d'argument $\frac{\pi}{2}$.
- Le temps d'attente en minute à un péage est une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda = 0,2$ (exprimé en min$^{-1}$). En moyenne une personne attend à ce péage :
- 2 min
- 5 min
- 10 min
- 20 min
On rappelle que si $X$ suit la loi expnentielle de paramètre $\lambda$ alors $E(X)=\dfrac{1}{\lambda}$. - La forme exponentielle du nombre complexe $z = - 3 + \text{i}3\sqrt{3}$ est :
- $3\text{e}^{\text{i}\frac{2\pi}{3}}$
- $6\text{e}^{\text{i}\frac{2\pi}{3}}$
- $6\text{e}^{-\text{i}\frac{2\pi}{3}}$
- $- 6\text{e}^{-\text{i}\frac{2\pi}{3}}$
- On considère le complexe $z = \sqrt{2} - \text{i}\sqrt{2}$. Le nombre complexe $z^2$ est égal à :
- $z^2 = 2$
- $z^2 = 4$
- $z^2 =- 4$
- $z^2 = - 4\text{i}$
On calcule $z^2$ : $$\begin{array}{rl} z^2&=\left( \sqrt{2} - \text{i}\sqrt{2}\right)^2\\ &= \sqrt{2}^2 -2\sqrt 2\times \text{i}\sqrt{2}+\text{i}^2\sqrt{2}^2\\ &= 2 - 4\text{i}-2\\ &= - 4\text{i}\end{array}$$
Ici le temps d'attente moyen est $E(X)=\dfrac{1}{\lambda}=\dfrac{1}{0,2}=5$
La bonne réponse est le b.
Forme trigonométrique de \(z =-3 + 3 \sqrt{3}i\):
Module : \(|z|=\sqrt{a^2+b^2}=\sqrt{ 3^2+\left(3\sqrt{3}\right)^2}=\sqrt{36}=6\)
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}=- \dfrac{ 3}{ 6} = -\dfrac{1}{2} \\ \sin(\theta)=\dfrac{b}{r} = \dfrac{3\sqrt{3}}{2} =\dfrac{\sqrt{3}}{2} \end{array} \right.$$ Ainsi \(\theta=\dfrac{2\pi}{3}\) convient; on a donc: $$z=\left[6;\dfrac{2\pi}{3}\right] \text{ ou } z=6\left [\cos\left (\dfrac{2\pi}{3}\right )+i\sin\left (\dfrac{2\pi}{3}\right )\right ]$$
La bonne réponse est le b.
La bonne réponse est le d.
Exercice 2 5 points
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Dans cet exercice, ln désigne la fonction logarithme népérien.
Partie A
On considère la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = ax + b\ln (x) + 1\] où $a$ et $b$ sont deux nombres réels. $C_f$ est la représentation graphique de la fonction $f$ dans un repère orthonormé. Les points A et E sont deux points de la courbe $C_f$. Le point A a pour coordonnées $(1~;~2)$ et le point E a pour abscisse 4. La tangente à $C_f$ au point E est horizontale. 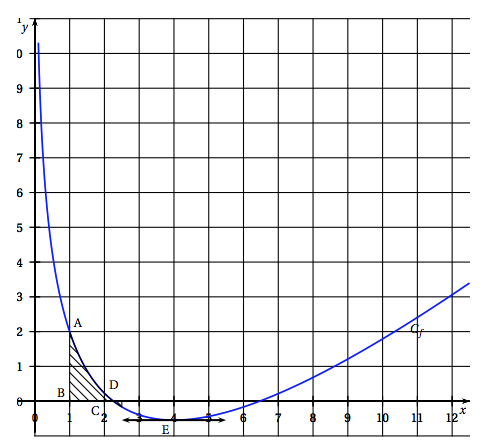
- Déterminer $f(1)$ et $f'(4)$ où $f'$ désigne la fonction dérivée de $f$.
- Calculer $f'(x)$ puis exprimer $f'(4)$ en fonction de $a$ et $b$.
- Déterminer les valeurs de $a$ et $b$.
Partie B
Soit la fonction $f$ définie sur $]0~;~+ \infty[$ par: \[f(x) = x - 4\ln (x) + 1\]
- Déterminer $\displaystyle\lim_{x \to 0} f(x)$ en justifiant la réponse. Donner une interprétation graphique du résultat.
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$ en justifiant la réponse (on pourra factoriser l'expression de $f(x)$ par $x$).
- Calculer la dérivée $f'$ de $f$. En déduire le tableau des variations de $f$.
Partie C
Une entreprise fabrique des pièces de carrosserie de voiture.
La forme d'une pièce est donnée sur la figure ci-contre et correspond à la zone hachurée sur le graphique de la page précédente. On souhaite déterminer la mesure de l'aire de la pièce en unité d'aire. Le point D est le point de la courbe $C_f$ d'abscisse 2. Les points B et C ont pour coordonnées respectives $(1~;~0)$ et $(2~;~0)$. 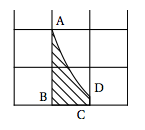
Soit la fonction $G$ définie sur $]0~;~+ \infty[$ par : \[G(x) = x\ln (x) - x.\]
- Calculer la dérivée $G'$ de $G$.
- En déduire une primitive $F$ de la fonction $f$ donnée dans la partie B sur $]0~;~+ \infty[$.
- Déterminer la valeur exacte de l'aire de la pièce en unité d'aire ; puis en donner une valeur arrondie à $10^{-2}$.
Correction de l'exercice 2 (5 points)
Exercice 2 5 points
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Dans cet exercice, ln désigne la fonction logarithme népérien.
Partie A
On considère la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = ax + b\ln (x) + 1\] où $a$ et $b$ sont deux nombres réels. $C_f$ est la représentation graphique de la fonction $f$ dans un repère orthonormé. Les points A et E sont deux points de la courbe $C_f$. Le point A a pour coordonnées $(1~;~2)$ et le point E a pour abscisse 4. La tangente à $C_f$ au point E est horizontale. 
- Déterminer $f(1)$ et $f'(4)$ où $f'$ désigne la fonction dérivée de $f$. Comme $A(1; 2)\in C_f$; on déduit que $f(1)= 2$
- Calculer $f'(x)$ puis exprimer $f'(4)$ en fonction de $a$ et $b$. Ayant $f(x) = ax + b\ln (x) + 1$, on déduit : $$f'(x)= a+b\times \dfrac{1}{x}$$ En effet $\left(\ln x\right)'= \dfrac{1}{x}$
- Déterminer les valeurs de $a$ et $b$. $$f(2)=1\iff a+b\ln 1 + 1 =2 \iff a+1 = 2\iff a = 1$$ $$f'(4) = 0\iff a +\dfrac{b}{4}= 0 \iff \dfrac{b}{4}= -1\iff b =-4$$
La tangente à $C_f$ au point d'abscisse 4 est horizontale, donc $f'(4)=0$.
$$f'(4)= a+\dfrac{b}{4}$$
$a = 1$ et $b =-4$
Partie B
Soit la fonction $f$ définie sur $]0~;~+ \infty[$ par: \[f(x) = x - 4\ln (x) + 1\]
- Déterminer $\displaystyle\lim_{x \to 0} f(x)$ en justifiant la réponse. Donner une interprétation graphique du résultat. $\left.\begin{array}{l} \lim\limits_{x \to 0}~x+1=1\\ \lim\limits_{x \to 0}~-\ln x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to 0}f(x)=+\infty$ Comme $\lim\limits_{x \to 0}f(x)=+\infty$ on déduit que la droite d'équation $x=0$ est asymptote verticale à $C_f$
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$ en justifiant la réponse (on pourra factoriser l'expression de $f(x)$ par $x$). On écrit $f(x) = x\left(1+ \dfrac{1}{x}- \dfrac{\ln x}{x}\right)$ On utilise la limite de référence : $\displaystyle\lim_{x \to + \infty}\dfrac{\ln x}{x}= 0$
- Calculer la dérivée $f'$ de $f$. En déduire le tableau des variations de $f$. $$\begin{array}{rl}f'(x)&= 1-\dfrac{4}{x}\\ &=\dfrac{x}{x}-\dfrac{4}{x}\\ &=\dfrac{x-4}{x} \end{array}$$ On étudie alors le signe de la dérivée sur $]0~;~+ \infty[$
- Calculer la dérivée $G'$ de $G$. $$G(x) = x\ln (x) - x=x\left( \ln x -1\right)$$ $G=uv$ , donc $G'=u'v+v'u$ $$\begin{array}{rl}G'(x)&= 1\left( \ln x -1\right) +x\times \dfrac{4}{x} \\ &= \ln x -1 +1 \\ &=\ln x \end{array}$$
- En déduire une primitive $F$ de la fonction $f$ donnée dans la partie B sur $]0~;~+ \infty[$. On a $$\begin{array}{rl}f(x)&= x - 4\ln (x) + 1\\ &= x+1- 4\ln x \\ &=x+1-4G'(x) \end{array}$$ Une primitive de $f$ est donc la fonction $F$ définie sur $]0~;~+ \infty[$ par : $$\begin{array}{rl} F(x)&= \dfrac{x^2}{2}+x-4G(x)\\ &= \dfrac{x^2}{2}+x-4\left(x\ln (x) - x\right)\\ &= \dfrac{x^2}{2}+5x-4x\ln (x) \end{array}$$
- Déterminer la valeur exacte de l'aire de la pièce en unité d'aire ; puis en donner une valeur arrondie à $10^{-2}$. D'après le grahique $C_f$ est située au desssus de l'axe des abscisses sur $[1; 2]$ , ainsi $f$ est continue et positive sur $[1; 2]$. L' aire de la piéce exprimée en unités d'aires vaut donc : $$\begin{array}{rl} A&= \int_1^2 f(x) dx\\ &= F(2)-F(1)\\ F(2)&= \dfrac{2^2}{2}+5\times 2-4\times 2\ln 2\\ &= 12-8\ln 2\\ F(1)&= \dfrac{1^2}{2}+5\times 1-4 \ln 1\\ &= \dfrac{11}{2}\\ &\\ A&= 12-8\ln 2- \dfrac{11}{2}\\ A&= \dfrac{13}{2}-8\ln 2 \\ \end{array}$$
- Sur les emballages, il est précisé que la masse des plats préparés est de $400$ grammes. Un plat est conforme lorsque sa masse, exprimée en gramme, est supérieure à $394$ grammes. On note $M$ la variable aléatoire qui, à chaque plat prélevé au hasard dans la production, associe sa masse en gramme. On suppose que la variable aléatoire $M$ suit la loi normale d'espérance $400$ et d'écart type $5$.
- Déterminer la probabilité qu'un plat prélevé au hasard ait une masse comprise entre $394$ et $404$ grammes.
- Déterminer la probabilité qu'un plat soit conforme.
- Les plats préparés sont livrés à un supermarché par lot de $300$. On arrondit la probabilité de l'évènement « un plat préparé prélevé au hasard dans la production n'est pas conforme » à $0,12$. On prélève au hasard $300$ plats dans la production. La production est assez importante pour que lion puisse assimiler ce prélèvement à un tirage aléatoire avec remise. On considère la variable aléatoire $X$ qui, à un lot de $300$ plats, associe le nombre de plats préparés non conformes qu'il contient.
- Justifier que la variable aléatoire $X$ suit une loi binomiale dont on précisera les paramètres.
- Calculer l'espérance mathématique E$(X)$ et en donner une interprétation.
- Calculer la probabilité que dans un échantillon de $300$ plats prélevés au hasard, au moins $280$ plats soient conformes.
- Le fabricant annonce sur les étiquettes de ses produits une proportion de produits non conformes de 12%. On prélève au hasard dans la production un échantillon de taille 1200 dans lequel $150$ plats se révèlent être non conformes.
- Quelle est la fréquence de plats non conformes dans l'échantillon prélevé ?
- Déterminer l'intervalle de fluctuation avec un niveau de confiance de 95% de la fréquence de plats non conformes dans un échantillon de taille 1200 .
Rappel : Lorsque la proportion $p$ dans la population est connue, l'intervalle de fluctuation asymptotique à $95$% d'une fréquence obtenue sur un échantillon de taille $n$ est : \[I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{n}}\right]\] - L'échantillon est-il représentatif de la production du fabricant ? Justifier.
- Sur les emballages, il est précisé que la masse des plats préparés est de $400$ grammes. Un plat est conforme lorsque sa masse, exprimée en gramme, est supérieure à $394$ grammes. On note $M$ la variable aléatoire qui, à chaque plat prélevé au hasard dans la production, associe sa masse en gramme. On suppose que la variable aléatoire $M$ suit la loi normale d'espérance $400$ et d'écart type $5$.
- Déterminer la probabilité qu'un plat prélevé au hasard ait une masse comprise entre $394$ et $404$ grammes.
- Déterminer la probabilité qu'un plat soit conforme. Selon le modèle de calculatrice utilisée, la réponse est immédiate :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$La probabilité qu'un plat prélevé au hasard ait une masse comprise entre 394 et 404 grammes est 0,673.2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$La probabilité qu'un plat soit conforme est 0,885. - Les plats préparés sont livrés à un supermarché par lot de $300$. On arrondit la probabilité de l'évènement « un plat préparé prélevé au hasard dans la production n'est pas conforme » à $0,12$. On prélève au hasard $300$ plats dans la production. La production est assez importante pour que lion puisse assimiler ce prélèvement à un tirage aléatoire avec remise. On considère la variable aléatoire $X$ qui, à un lot de $300$ plats, associe le nombre de plats préparés non conformes qu'il contient.
- Justifier que la variable aléatoire $X$ suit une loi binomiale dont on précisera les paramètres. On assimile ce prélèvement à un tirage aléatoire avec remise donc la variable aléatoire $X$ suit la loi binomiale de paramètres $n=300$ et $p=0,12$.
- Calculer l'espérance mathématique E$(X)$ et en donner une interprétation. $E(X)=300\times 0,12=36$
- Calculer la probabilité que dans un échantillon de $300$ plats prélevés au hasard, au moins $280$ plats soient conformes. L'évènement « au moins 280 plats sont conformes » est l'èvènement contraire de l'événement « 19 plats au plus ne sont pas conformes » Avec la calculatrice, on trouve : $P(X\geq 280)=1-P(X\leq 19)\approx 0,999$
Dans un lot de 300 plats on trouve en moyenne 36 plats non conformes.2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$La probabilité que dans un échantillon de 300 plats prélevés au hasard, au moins 280 plats soient conformes est 0,999. - Le fabricant annonce sur les étiquettes de ses produits une proportion de produits non conformes de 12%. On prélève au hasard dans la production un échantillon de taille 1200 dans lequel $150$ plats se révèlent être non conformes.
- Quelle est la fréquence de plats non conformes dans l'échantillon prélevé ? La frequence de plats non conformes dans l'échantillon prélevé est $f=\dfrac{150}{1200}=0,125$.
- Déterminer l'intervalle de fluctuation avec un niveau de confiance de 95% de la fréquence de plats non conformes dans un échantillon de taille 1200 .
Rappel : Lorsque la proportion $p$ dans la population est connue, l'intervalle de fluctuation asymptotique à $95$% d'une fréquence obtenue sur un échantillon de taille $n$ est : \[I = \left[p - 1,96\sqrt{\dfrac{p(1 - p)}{n}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{n}}\right]\] - L'échantillon est-il représentatif de la production du fabricant ? Justifier.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$Soit avec des valeurs approchées à $10^{-3 }$ près des bornes de l'intervalle, l'intervalle de fluctuation avec un niveau de confiance de 95 % de la fréquence de plats non conformes dans un échantillon de taille 1 200 est $I=[0,1010,139]$.La fréquence de plats non conformes dans l'échantillon prélevé appartient à l'intervalle de fluctuation asymptotique au seuil de 95% donc cet échantillon est représentatif de la production du fabricant. -
- Montrer que $u_1 = 0,914 u_0$.
- Si l'équipe de direction tient ses engagements, quel sera le déficit de la multinationale en 2016 ?
- Démontrer que la suite $\left(u_n\right)$ est géométrique, puis exprimer $u_n$ en fonction de $n$.
-
- Résoudre l'inéquation suivante d'inconnue l'entier naturel $n$ : \[0,914^n \leqslant \dfrac{1}{3}\]
- Quand l'engagement de l'équipe de direction, à savoir ramener le déficit de la multinationale au-dessous des 5 millions d'euros, sera-t-il atteint ?
- On considère l'algorithme ci-dessous qui permet de retrouver le résultat de la question précédente. $$ \begin{array}{|l X|}\hline \text{Variables} &\\ &N \text{ un entier naturel}\\ &Q \text{ et } U \text{ deux nombres réels.}\\ \text{Début} &\\ &N \text{ prend la valeur } 0\\ &Q \text{ prend la valeur } 0,914\\ &U \text{ prend la valeur } 15\\ &\text{Tant que ... faire}\\ &\hspace{0.5cm}\begin{array}{|l} N \text{ prend la valeur } \ldots\\ U \text{ prend la valeur } \ldots \end{array}\\ &\text{Fin Tant que}\\ &\text{ Afficher } \ldots\\ \text{Fin} &\\ \hline \end{array} $$
- Recopier et compléter les lignes en pointillé afin que l'algorithme renvoie l'année à partir de laquelle le déficit de cette multinationale sera ramené en dessous de $5$ millions d'euros.
- On suppose l'algorithme complété. Proposer une modification de l'algorithme afin que celui-ci affiche le montant du déficit de cette multinationale chaque année jusqu'à ce que celui-ci soit ramené au-dessous de $5$ millions d'euros.
-
- Calculer la somme des déficits sur onze ans à partir de l'année 2014 comprise, c'est-à-dire : $u_0 + u_1 + u_2 + \cdots + u_{10}$·
- Construire un algorithme qui donne cette somme en sortie.
-
- Montrer que $u_1 = 0,914 u_0$. En 2015 le montant du déficit baisse de 8,6 % soit : $$u_1=u_0\times 1-\dfrac{8,6}{100}=u_0\times0,914$$
- Si l'équipe de direction tient ses engagements, quel sera le déficit de la multinationale en 2016 ? Après deux baisses successives de 8,6 %, en 2016 le montant du déficit serait de : $$u_2=15\times0,914\times0,914\approx 12,531$$
- Démontrer que la suite $\left(u_n\right)$ est géométrique, puis exprimer $u_n$ en fonction de $n$. Pour tout entier $n$ on a : $u_{n+1}=u_n\times 0,914$ donc $(u_n )$ est une suite géométrique de raison 0,914.
Ainsi, $u_1=0,914u_0$.En 2016, le déficit serait d'environ 12,531 millions d'euros.
$(u_n )$ est une suite géométrique de raison 0,914 et de premier terme $u_0=15$ donc :pour tout entier $n, u_n=15\times 0,914^n.$ -
- Résoudre l'inéquation suivante d'inconnue l'entier naturel $n$ : \[0,914^n \leqslant \dfrac{1}{3}\] $$\begin{array}{rll} 0,914^n \leqslant \dfrac{1}{3}& \iff \ln\left (0,914^n\right ) \leqslant \ln\left (\dfrac{1}{3} \right ) & \text{ car } \ln \text{ est strictement croissante } \\ && \text{ sur } ]0; +\infty[ \\ &\iff n \ln\left (0,914 \right ) \leqslant -\ln 3 & \text{ car } \ln\left (a^n\right )=n\ln a \text{ et } \ln\left (\dfrac{1}{a} \right )=-\ln a\\ &\iff n\geq \dfrac{-\ln 3}{\ln\left (0,914 \right )}& \text{ car } 0,914< 1 \text{ ainsi } \ln\left (0,914 \right )< 0\\ \end{array}$$ Comme $\dfrac{-\ln 3}{\ln\left (0,914 \right )}\approx 12,2$ alors :
- Quand l'engagement de l'équipe de direction, à savoir ramener le déficit de la multinationale au-dessous des 5 millions d'euros, sera-t-il atteint ? On cherche le plus petit entier $n$ solution de l'inéquation
les solutions entières de l'inéquation $0,914^n \leqslant \dfrac{1}{3}$ sont les entiers $n\geq 13. .$Le déficit de la multinationale sera inférieur à 5 millions d'euros à partir de 2027. - On considère l'algorithme ci-dessous qui permet de retrouver le résultat de la question précédente. $$ \begin{array}{|l X|}\hline \text{Variables} &\\ &N \text{ un entier naturel}\\ &Q \text{ et } U \text{ deux nombres réels.}\\ \text{Début} &\\ &N \text{ prend la valeur } 0\\ &Q \text{ prend la valeur } 0,914\\ &U \text{ prend la valeur } 15\\ &\text{Tant que ... faire}\\ &\hspace{0.5cm}\begin{array}{|l} N \text{ prend la valeur } \ldots\\ U \text{ prend la valeur } \ldots \end{array}\\ &\text{Fin Tant que}\\ &\text{ Afficher } \ldots\\ \text{Fin} &\\ \hline \end{array} $$
- Recopier et compléter les lignes en pointillé afin que l'algorithme renvoie l'année à partir de laquelle le déficit de cette multinationale sera ramené en dessous de $5$ millions d'euros. $$ \begin{array}{|l X|}\hline \text{Variables} &\\ &N \text{ un entier naturel}\\ &Q \text{ et } U \text{ deux nombres réels.}\\ \text{Début} &\\ &N \text{ prend la valeur } 0\\ &Q \text{ prend la valeur } 0,914\\ &U \text{ prend la valeur } 15\\ &\text{Tant que } U > 5 \text{ faire }\\ &\hspace{0.5cm}\begin{array}{|l} N \text{ prend la valeur } N+1 \\ U \text{ prend la valeur } 0,914\times U \end{array}\\ &\text{Fin Tant que}\\ &\text{ Afficher } 2014+N\\ \text{Fin} &\\ \hline \end{array} $$
- On suppose l'algorithme complété. Proposer une modification de l'algorithme afin que celui-ci affiche le montant du déficit de cette multinationale chaque année jusqu'à ce que celui-ci soit ramené au-dessous de $5$ millions d'euros. $$ \begin{array}{|l X|}\hline \text{Variables} &\\ &N \text{ un entier naturel}\\ &Q \text{ et } U \text{ deux nombres réels.}\\ \text{Début} &\\ &N \text{ prend la valeur } 0\\ &Q \text{ prend la valeur } 0,914\\ &U \text{ prend la valeur } 15\\ &\text{Tant que } U > 5 \text{ faire }\\ &\hspace{0.5cm}\begin{array}{|l} N \text{ prend la valeur } N+1 \\ U \text{ prend la valeur } 0,914\times U \end{array}\\ &\text{Fin Tant que}\\ &\text{ Afficher « Déficit en } 2014+N \text{ »} = U\\ \text{Fin} &\\ \hline \end{array} $$
-
- Calculer la somme des déficits sur onze ans à partir de l'année 2014 comprise, c'est-à-dire : $u_0 + u_1 + u_2 + \cdots + u_{10}$· $(u_n)$ est une suite géométrique de raison 0,914 et de premier terme $u_0=15 $ donc la somme des 11 premiers termes de cette suite est : $$\begin{array}{rl} u_0+u_1+u_2+\cdots +u_{10}&= \dfrac{1-\text{ Raison}^{\text{ Nombres de termes}}}{1-\text{ Raison}}\times \text{ Premier terme}\\ & \dfrac{1-0,914^{11}}{1-0,914}\times 15\\ &\approx 109,555 \end{array}$$
- Construire un algorithme qui donne cette somme en sortie. $$ \begin{array}{|l X|}\hline \text{Variables} &\\ &N \text{ un entier naturel}\\ &Q \text{ et } S \text{ et } U \text{ deux nombres réels.}\\ \text{Début} &\\ &N \text{ prend la valeur } 0\\ &Q \text{ prend la valeur } 0,914\\ &U \text{ prend la valeur } 15\\ &S \text{ prend la valeur } 15\\ &\text{Pour } N \text{ allant de } 1 \text{ à } 10\\ &\hspace{0.5cm}\begin{array}{|l} U \text{ prend la valeur } 0,914\times U \\ S \text{ prend la valeur } S+U \end{array}\\ &\text{Fin Pour}\\ &\text{ Afficher } S &\\ \hline \end{array} $$
En 11 ans, le déficit cumulé est d'environ 109,555 millions d'euros. - une source de tension continue $E$ de 10 V.
- une résistance $R$ de $10^5$\: $\Omega$.
- un condensateur de capacité $C$ de $10^{-6}$ F.
- Justifier que l'équation différentielle est équivalente à : \[u' + 10u = 100\]
-
- Déterminer la forme générale $u(t)$ des solutions de cette équation différentielle.
- On considère qu'à l'instant $t = 0$, le condensateur est déchargé. Parmi les solutions, déterminer l'unique fonction $u$ tel que $u(0) = 0$.
- Déterminer en justifiant la réponse, la limite en $+ \infty$ de la fonction $u$ ainsi obtenue. En donner une interprétation.
- On donne ci-dessous la représentation graphique de la fonction $u$ qui vient d'être obtenue à la question 2. b. avec les unités suivantes : 1 unité pour 1 seconde sur l'axe des abscisses et 1 unité pour 1 volt sur l'axe des ordonnées. On appelle $T$ le temps de charge en seconde pour que $u(T)$ soit égal à $95$% de $E$.
- Déterminer graphiquement le temps de charge $T$.
- Retrouver, par le calcul, le résultat précédent.
- Sans modifier les valeurs respectives de $E$ et de $C$, déterminer la valeur de $R$ afin que le temps de charge $T$ soit multiplié par $2$.
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~1+ \dfrac{1}{x}=1\\ \lim\limits_{x \to +\infty}~- \dfrac{\ln x}{x}=0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to+\infty}1+ \dfrac{1}{x}- \dfrac{\ln x}{x}=1$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~x=+\infty\\ \lim\limits_{x \to +\infty}~1+ \dfrac{1}{x}- \dfrac{\ln x}{x}=1 \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to+\infty}f(x)=+\infty$
$\lim\limits_{x \to+\infty}f(x)=+\infty$
On peut par exemple faire un tableau de signes:
$$\begin{array}{|l|cccccr|} \hline x &0& & & 4 & & &+\infty\\
\hline \text{ Signe de } x& 0& & + & & + && \\ \hline \text{ Signe de } x-4 && & - & 0 & + &&\\ \hline \text{ Signe de } f'(x) & \| && - & 0 &+ & & \\ \hline \end{array}$$
On peut aussi plus simplement remarquer que sur $]0~;~+ \infty[$, on a $x> 0$, et donc $f'(x)$ a le signe de $x-4$, on dresse alors le tableau de variations de $f$ : 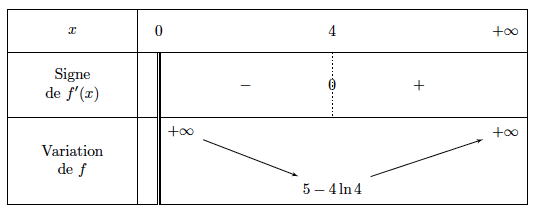
Partie C
Une entreprise fabrique des pièces de carrosserie de voiture.
La forme d'une pièce est donnée sur la figure ci-contre et correspond à la zone hachurée sur le graphique de la page précédente. On souhaite déterminer la mesure de l'aire de la pièce en unité d'aire. Le point D est le point de la courbe $C_f$ d'abscisse 2. Les points B et C ont pour coordonnées respectives $(1~;~0)$ et $(2~;~0)$. 
Soit la fonction $G$ définie sur $]0~;~+ \infty[$ par : \[G(x) = x\ln (x) - x.\]
Exercice 3 4 points
Étude de la production de plats préparés sous vide.
Les questions 1, 2 et 3 de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-3}$
L'entreprise BUENPLATO produit en grande quantité des plats préparés sous vide. L'objectif de cet exercice est d'analyser la qualité de cette production en exploitant divers outils mathématiques.
Correction de l'exercice 3 (5 points)
Étude de la production de plats préparés sous vide.
Les questions 1, 2 et 3 de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-3}$
L'entreprise BUENPLATO produit en grande quantité des plats préparés sous vide. L'objectif de cet exercice est d'analyser la qualité de cette production en exploitant divers outils mathématiques.
Exercice 4 4 points
Étude du déficit d'une multinationale
Le déficit d'une multinationale a été de 15 millions d'euros en 2014. Devant l'ampleur de ce déficit, l'équipe de direction décide de prendre des mesures afin de ramener ce déficit annuel à moins de $5$ millions d'euros. Jusqu'à ce que cet objectif soit atteint, cette équipe s'engage à ce que le déficit baisse de 8,6% tous les ans. On définit la suite $\left(u_n\right)$ de la manière suivante : on note $u_n$ le déficit en million d'euros de cette multinationale lors de l'année $2014 + n$. Ainsi $u_0 = 15$. Dans tout l'exercice, les résultats seront arrondis à $10^{-3}$.
Exercice 4 4 points
Étude du déficit d'une multinationale
Le déficit d'une multinationale a été de 15 millions d'euros en 2014. Devant l'ampleur de ce déficit, l'équipe de direction décide de prendre des mesures afin de ramener ce déficit annuel à moins de $5$ millions d'euros. Jusqu'à ce que cet objectif soit atteint, cette équipe s'engage à ce que le déficit baisse de 8,6% tous les ans. On définit la suite $\left(u_n\right)$ de la manière suivante : on note $u_n$ le déficit en million d'euros de cette multinationale lors de l'année $2014 + n$. Ainsi $u_0 = 15$. Dans tout l'exercice, les résultats seront arrondis à $10^{-3}$.
Exercice 5 4 points
On étudie la charge d'un condensateur et l'on dispose pour cela du circuit électrique ci-contre composé de :
On note $u$ la tension exprimée en volt aux bornes du condensateur. Cette tension $u$ est une fonction du temps $t$ exprimé en seconde. La fonction $u$ est définie et dérivable sur $[0~;~+oo[$ ; elle vérifie l'équation différentielle suivante : \[RCu' + u = E\] où $u'$ est la fonction dérivée de $u$. 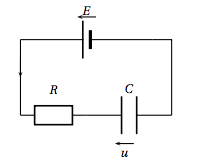
Exercice 5 4 points
On étudie la charge d'un condensateur et l'on dispose pour cela du circuit électrique ci-contre composé de :
- une source de tension continue $E$ de 10 V.
- une résistance $R$ de $10^5$\: $\Omega$.
- un condensateur de capacité $C$ de $10^{-6}$ F.
On note $u$ la tension exprimée en volt aux bornes du condensateur. Cette tension $u$ est une fonction du temps $t$ exprimé en seconde. La fonction $u$ est définie et dérivable sur $[0~;~+oo[$ ; elle vérifie l'équation différentielle suivante : \[RCu' + u = E\] où $u'$ est la fonction dérivée de $u$. 
- Justifier que l'équation différentielle est équivalente à : \[u' + 10u = 100\] Avec $R=10^5, C=10^{-6}$ et $R=10$, la fonction $u$ vérifie l'équation différentielle suivante : $$\begin{array}{rl} RCu' + u = E & \iff 10^5\times 10^{-6}u'+ u = 10 \\ & \iff 10^{-1}u'+ u = 10 \\ &\iff u′+10u=100 \end{array}$$ Ainsi, la fonction u vérifie l'équation différentielle $u′+10u=100$
-
- Déterminer la forme générale $u(t)$ des solutions de cette équation différentielle. Les solutions de l'équation différentielle $y′=ay+b$ sont les fonctions définies sur $\mathbb R$ par $x\mapsto ke^{ax}-\frac{b}{a}$, où $k$ est une constante réelle quelconque. Ici $u′+10u=100 \iff u’= -10u+100$ est du type $y′=ay+b$ où $a= -10$ et $b= 100$, on a $-\frac{b}{a}= -\frac{100}{-10}= 10$.
- On considère qu'à l'instant $t = 0$, le condensateur est déchargé. Parmi les solutions, déterminer l'unique fonction $u$ tel que $u(0) = 0$. La condition $u(0)=0$ équivaut à $ke^0+10=0$ d'où $k=-10$
- Déterminer en justifiant la réponse, la limite en $+ \infty$ de la fonction $u$ ainsi obtenue. En donner une interprétation. $\left.\begin{array}{l} \lim\limits_{t \to +\infty}~(-10t)=-\infty\\ \lim\limits_{X \to-\infty}~e^X=0 \end{array}\right\} \quad \text{ Par composée } \lim\limits_{t \to +\infty}~e^{-10t}=0$ puis $\lim\limits_{t \to +\infty}~10-10e^{-10t}=10$
Les solutions sur $[0;+\infty[$ de l'équation différentielle $u′=- 10u+100$ sont les fonctions définies sur $[0;+\infty[$ par $u(t)=ke^{-10t}+10 $ où $k$ est une constante réelle quelconque.La fonction $u$ est définie sur $[0;+\infty[$ par $u(t)=-10e^{-10t}+10 $Ainsi $\lim\limits_{t \to +\infty}~u(t)=10$.
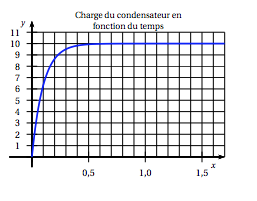
À partir d'un certain temps, la tension aux bornes du condensateur est très proche de 10 volts. - On donne ci-dessous la représentation graphique de la fonction $u$ qui vient d'être obtenue à la question 2. b. avec les unités suivantes : 1 unité pour 1 seconde sur l'axe des abscisses et 1 unité pour 1 volt sur l'axe des ordonnées. On appelle $T$ le temps de charge en seconde pour que $u(T)$ soit égal à $95$% de $E$.
- Déterminer graphiquement le temps de charge $T$.
- Retrouver, par le calcul, le résultat précédent. $$\begin{array}{rl} -10e^{-10t}+10 = 0,95\times 10 &\iff -10e^{-10t} = -0,5 \\ &\iff e^{-10t} = 0,05 \\ &\iff \ln \left( e^{-10t}\right) = \ln(0,05 ) \\ &\iff -10t = \ln(0,05 ) \\ &\iff t = -0,1 \ln(0,05 ) \\ \end{array}$$
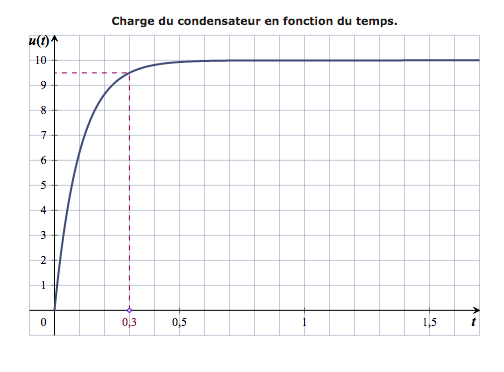 Le temps de charge T est d'environ 0,3 secondes.Le temps de charge en seconde pour que $u(T)$ soit égal à 95 % de $E$ est $t = -0,1 \ln(0,05 )$ soit environ 0,3 secondes.
Le temps de charge T est d'environ 0,3 secondes.Le temps de charge en seconde pour que $u(T)$ soit égal à 95 % de $E$ est $t = -0,1 \ln(0,05 )$ soit environ 0,3 secondes. - Sans modifier les valeurs respectives de $E$ et de $C$, déterminer la valeur de $R$ afin que le temps de charge $T$ soit multiplié par $2$.
- Soit $v$ la tension exprimée en volt aux bornes du condensateur, la fonction $v$ vérifie l'équation différentielle suivante : $$R\times 10^{-6}v′+v=10\iff v′=-\frac{10^6}{R}v+\frac{10^7}{R}$$
- Les solutions de cette équation différentielle sont les fonctions définies sur $[0;+\infty[$ par $v(t)=ke^{-\frac{10^6}{R}t}+10$ où $k$ est une constante réelle quelconque.
- La condition $v(0)=0$ équivaut à $ke^0+10=0$ d'où $k=-10.$
- Par conséquent, la fonction $v$ est définie sur $[0;+\infty[$ par $v(t)=-10e^{-\frac{10^6}{R}t}+10$ Le temps de charge $T$ est multiplié par 2 pour $R$ solution de l'équation $$\begin{array}{rl} -10e^{- \frac{10^6}{R}\times 2T }+10 = 10-10 e^{-10T}&\iff e^{- \frac{10^6}{R}\times 2T } = e^{-10T}\\ &\iff - \frac{10^6}{R}\times 2T =-10T \\ &\iff \\ &\iff - \frac{10^6}{R}= -10\\ &\iff R= 2\times 10^5 \end{array}$$
- Vues: 25109
