Bac STI2D Antilles Guyane 22 juin 2015 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 5 points

Fonction $\ln$

Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Dans cet exercice, ln désigne la fonction logarithme népérien.

Partie A

On considère la fonction $f$ définie sur $]0~;~+ \infty[$ par : \[f(x) = ax + b\ln (x) + 1\] où $a$ et $b$ sont deux nombres réels. $C_f$ est la représentation graphique de la fonction $f$ dans un repère orthonormé. Les points A et E sont deux points de la courbe $C_f$. Le point A a pour coordonnées $(1~;~2)$ et le point E a pour abscisse 4. La tangente à $C_f$ au point E est horizontale.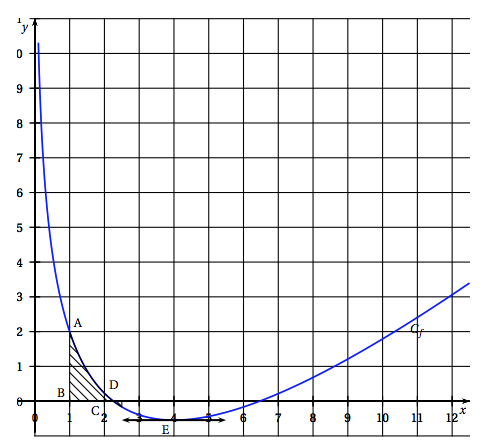

1. Déterminer $f(1)$ et $f'(4)$ où $f'$ désigne la fonction dérivée de $f$.
2. Calculer $f'(x)$ puis exprimer $f'(4)$ en fonction de $a$ et $b$.
3. Déterminer les valeurs de $a$ et $b$.

 

Partie B

Soit la fonction $f$ définie sur $]0~;~+ \infty[$ par: \[f(x) = x - 4\ln (x) + 1\]

1. Déterminer $\displaystyle\lim_{x \to 0} f(x)$ en justifiant la réponse. Donner une interprétation graphique du résultat.
2. Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$ en justifiant la réponse (on pourra factoriser l'expression de $f(x)$ par $x$).
3. Calculer la dérivée $f'$ de $f$. En déduire le tableau des variations de $f$.

 

Partie C

Une entreprise fabrique des pièces de carrosserie de voiture.
La forme d'une pièce est donnée sur la figure ci-contre et correspond à la zone hachurée sur le graphique de la page précédente. On souhaite déterminer la mesure de l'aire de la pièce en unité d'aire. Le point D est le point de la courbe $C_f$ d'abscisse 2. Les points B et C ont pour coordonnées respectives $(1~;~0)$ et $(2~;~0)$.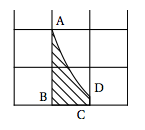

Soit la fonction $G$ définie sur $]0~;~+ \infty[$ par : \[G(x) = x\ln (x) - x.\]

1. Calculer la dérivée $G'$ de $G$.
2. En déduire une primitive $F$ de la fonction $f$ donnée dans la partie B sur $]0~;~+ \infty[$.
3. Déterminer la valeur exacte de l'aire de la pièce en unité d'aire ; puis en donner une valeur arrondie à $10^{-2}$.