Baccalauréat S -- Nouvelle Calédonie 27 novembre 2018 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (6 points)
Soit ABCDEFGH le cube représenté ci-dessous.
On considère:
- I et J les milieux respectifs des segments [AD] et [BC];
- P le centre de la face ABFE, c'est-à-dire l'intersection des diagonales (AF) et (BE);
- Q le milieu du segment [FG].
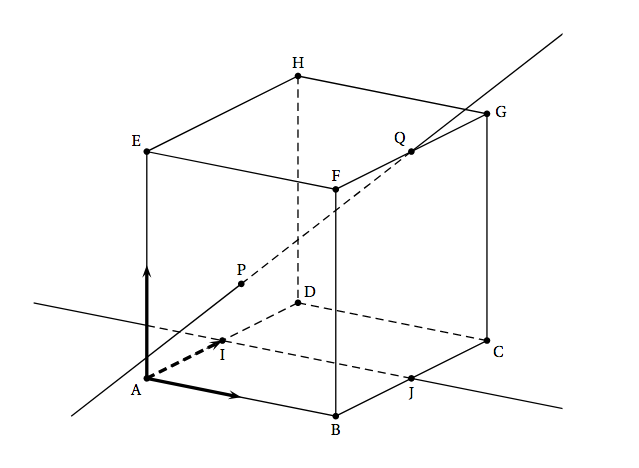
On se place dans le repère orthonormé $\left ( \text{A}~;~\frac{1}{2}\vec{AB}\;,\;\frac{1}{2}\vec{AD}\;,\;\frac{1}{2}\vec{AE}\right )$. Dans tout l'exercice, on pourra utiliser les coordonnées des points de la figure sans les justifier.
On admet qu'une représentation paramétrique de la droite (IJ) est \[\left \lbrace \begin{array}{l !{=} l} x& r\\ y & 1\\ z & 0\\ \end{array} \right . , \quad r\in\mathbb{R}\]
- Vérifier qu'une représentation paramétrique de la droite (PQ) est \[\left \lbrace \begin{array}{l !{=} r} x& 1+t\\ y & t \\ z & 1+t\\ \end{array} \right . ,\quad t\in\mathbb{R}\] Le point $P$ a pour coordonnées $(1;0;1)$.
-
- On admet qu'il existe un unique point K appartenant à la droite (IJ) tel que (MK) soit orthogonale à (IJ). Démontrer que les coordonnées de ce point K sont $(1+t~;~1~;~0)$. Les coordonnées du point $I$ sont $(0;1;0)$ et celles du point $J$ sont $(2;1;0)$.
- En déduire que $\text{MK} = \sqrt{2+2t^2}$.
Ainsi les coordonnées du vecteur $\vec{IJ}$ sont $(2;0;0)$.
On considère le point $K’$ de coordonnées $(1+t;1;0)$.
Alors les coordonnées du vecteur $\vec{MK’}$ sont $(0;1-t;-1-t)$.
$\vec{IJ}.\vec{MK’}=0+0+0=0$.
Les vecteurs $\vec{IJ}$ et $\vec{MK’}$ sont orthogonaux.
$\quad$
Une représentation paramétrique de la droite $(IJ)$ est $\begin{cases} x=r\\y=1\\z=0\end{cases}, \quad r\in \mathbb{R}$.
En prenant $r=1+t$ on obtient le fait que $K’$ appartient à la droite $(IJ)$.
$\quad$
Le point $K’$ appartient à la droite $(IJ)$ et est tel que $(MK’)$ soit orthogonal à $(IJ)$. Un tel point est unique d’après l’énoncé.
Par conséquent les coordonnées du point $K$ sont bien $(1+t;1;0)$.
$\quad$
$\begin{align*} MK&=\left\| \vec{MK}\right\| \\
&=\sqrt{0^2+(1-t)^2+(-1-t)^2} \\
&=\sqrt{1-2t+t^2+1+2t+t^2}\\
&=\sqrt{2+2t^2}\end{align*}$
$\quad$ -
- Vérifier que $y-z=0$ est une équation cartésienne du plan (HGB). Le point $H$ a pour coordonnées $(0;2;2)$ et $y_H-z_H=2-2=0$. Donc $H$ appartient au plan d’équation $y-z=0$.
- On admet qu'il existe un unique point L appartenant au plan (HGB) tel que (ML) soit orthogonale à (HGB).
Vérifier que les coordonnées de ce point L sont $\left (1+t~;~\dfrac{1}{2}+t~;~\dfrac{1}{2}+t\right )$. On note $L’$ le point de coordonnées $\left(1+t;\dfrac{1}{2}+t;\dfrac{1}{2}+t\right)$. - En déduire que la distance ML est indépendante de $t$.
Le point $G$ a pour coordonnées $(2;2;2)$ et $y_G-z_G=2-2=0$. Donc $G$ appartient au plan d’équation $y-z=0$.
Le point $B$ a pour coordonnées $(2;0;0)$ et $y_B-z_B=0-0=0$. Donc $B$ appartient au plan d’équation $y-z=0$.
Ainsi, une équation cartésienne du plan $(HGB)$ est $y-z=0$.
$\quad$
$y_L-z_L=\dfrac{1}{2}+t-\dfrac{1}{2}-t=0$ donc $L’$ appartient au plan $(HGB)$.
$\quad$
Les coordonnées du vecteur $\vec{ML’}$ sont $\left(0;\dfrac{1}{2}+t-t;\dfrac{1}{2}+t-1-t\right)$ soit $\left(0;\dfrac{1}{2};-\dfrac{1}{2}\right)$.
Un vecteur normal au plan $(HGB)$ est $\vec{n}(0;1;-1)$.
Par conséquent $\vec{ML’}=\dfrac{1}{2}\vec{n}$.
Le vecteur $\vec{ML’}$ est bien orthogonal au plan $(HGB)$.
$\quad$
Le point $L’$ appartient au plan $(HGB)$ et est tel que $(ML’)$ soit orthogonal à $(HGB)$. Un tel point est unique.
Les coordonnées du point $L$ sont donc $\left(0;\dfrac{1}{2}+t-t;\dfrac{1}{2}+t-1-t\right)$.
$\quad$
$\begin{align*} ML&=\left\| \vec{ML}\right\| \\
&=\sqrt{0^2+\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2} \\
&=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}\\
&=\sqrt{\dfrac{1}{2}}\\
&=\dfrac{\sqrt{2}}{2}\end{align*}$
$\quad$ - Existe-t-il une valeur de $t$ pour laquelle la distance MK est égale à la distance ML? On veut résoudre l’équation :
Le point $F$ a pour coordonnées $(2;0;2)$ et le point $G$ a pour coordonnées $(2;2;2)$.
Ainsi le point $Q$ a pour coordonnées $\left(\dfrac{2+2}{2};\dfrac{0+2}{2};\dfrac{2+2}{2}\right)$ soit $(2;1;2)$.
Dans la représentation paramétrique proposée :
$\bullet$ Si $t=0$ alors $\begin{cases} x=1\\y=0\\z=1\end{cases}$ et on obtient les coordonnées du point $P$.
$\bullet$ Si $t=1$ alors $\begin{cases} x=2\\y=1\\z=2\end{cases}$ et on obtient les coordonnées du point $Q$.
Une représentation paramétrique de la droite $(PQ)$ est donc bien $\begin{cases} x=1+t\\y=t\\z=1+t\end{cases}, \quad t\in \R$.
$\quad$
Soient $t$ un nombre réel et M $(1+t~;~t~;~1+t)$ le point de la droite (PQ) de paramètre $t$.
$ ML=MK \iff \sqrt{\dfrac{1}{2}}=\sqrt{2+2t^2}$
Or, pour tout réel $t$ on a $2+2t^2\geq 2>\dfrac{1}{2}$.
Il n’existe donc pas de valeur de $t$ pour laquelle la distance $MK$ est égale à la distance $ML$.
$\quad$
- Vues: 29788
