Baccalauréat S -- Nouvelle Calédonie 27 novembre 2018

Page 1 sur 10

 

Exercice 1 6 points

Commun à tous les candidats

Soient $f$ et $g$ les fonctions définies sur $]0~;~+\infty[$ par \[f(x)=\text{e} ^{-x}\quad \text{ et }\quad g(x) = \dfrac{1}{x^2} \text{e} ^{-\frac{1}{x}}.\] On admet que $f$ et $g$ sont dérivables sur $]0~;~+\infty[$. On note $f'$ et $g'$ leurs fonctions dérivées respectives. Les représentations graphiques de $f$ et $g$ dans un repère orthogonal, nommées respectivement $\mathcal{C}_f$ et $\mathcal{C}_g$ sont données ci-dessous: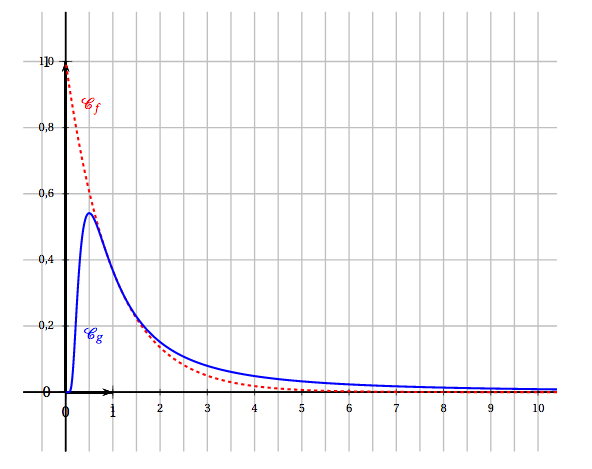

Partie A -- Conjectures graphiques

Dans chacune des questions de cette partie, aucune explication n'est demandée.

1. Conjecturer graphiquement une solution de l'équation $f(x)=g(x)$ sur $]0~;~+\infty[$.
2. Conjecturer graphiquement une solution de l'équation $g'(x)=0$ sur $]0~;~+\infty[$.

 

Partie B -- Étude de la fonction $g$

 

1. Calculer la limite de $g(x)$ quand $x$ tend vers $+\infty$.
2. On admet que la fonction $g$ est strictement positive sur $]0~;~+\infty[$. Soit $h$ la fonction définie sur $]0~;~+\infty[$ par $h(x)=\ln\left ( g(x) \strut\right )$.
   1. Démontrer que, pour tout nombre réel $x$ strictement positif, \[h(x)= \dfrac{-1-2x\ln x}{x}.\]
   2. Calculer la limite de $h(x)$ quand $x$ tend vers 0.
   3. En déduire la limite de $g(x)$ quand $x$ tend vers 0.
3. Démontrer que, pour tout nombre réel $x$ strictement positif, \[g'(x)= \dfrac{\text{e} ^{-\frac{1}{x}}\left (1-2x \strut\right )}{x^4}.\]
4. En déduire les variations de la fonction $g$ sur $]0~;~+\infty[$.

 

Partie C -- Aire des deux domaines compris entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$

 

1. Démontrer que la point A de coordonnées $\left (1~;~\text{e} ^{-1}\strut\right )$ est un point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$.
   On admet que ce point est l'unique point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$, et que $\mathcal{C}_f$ est au dessus de $\mathcal{C}_g$ sur l'intervalle $]0~;~1[$ et en dessous sur l'intervalle $]1~;~+\infty[$.
2. Soient $a$ et $b$ deux réels strictement positifs. Démontrer que \[\displaystyle\int_{a}^{b} \left ( f(x)-g(x)\strut\right ) \text{d} x = \text{e} ^{-a} + \text{e} ^{-\frac{1}{a}} - \text{e} ^{-b} - \text{e} ^{-\frac{1}{b}}.\]
3. Démontrer que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =1-2\text{e} ^{-1}.\]
4. On admet que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =\displaystyle\lim_{b\to +\infty} \displaystyle\int_{1}^{b} \left ( g(x)-f(x)\strut\right ) \text{d} x .\] Interpréter graphiquement cette égalité.