Baccalauréat S Pondichéry 4 mai 2018
Exercice 1 5 points
Les parties A et B peuvent être traitées de façon indépendante.
Dans une usine, un four cuit des céramiques à la température de 1000 ° C. À la fin de la cuisson, il est éteint et il refroidit.
On s'intéresse à la phase de refroidissement du four, qui débute dès l'instant où il est éteint.
La température du four est exprimée en degré Celsius ( °C).
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à $70$ °C. Sinon les céramiques peuvent se fissurer, voire se casser.
Partie A
Pour un nombre entier naturel $n$, on note $T_n$ la température en degré Celsius du four au bout de $n$ heures écoulées à partir de l'instant où il a été éteint. On a donc $T_0 = 1000 $. La température $T_n$ est calculée par l'algorithme suivant : $$ \begin{array}{|cc|}\hline T \gets 1000 \\ \text{ Pour } i \text{ allant de 1 à } n \\ \hspace{1cm} T \gets 0,82 \times T + 3,6 \\ \text{Fin Pour }\\\hline \end{array}$$
- Déterminer la température du four, arrondie à l'unité, au bout de $4$ heures de refroidissement.
- Démontrer que, pour tout nombre entier naturel $n$, on a : $T_n = 980 \times 0,82^n + 20$.
- Au bout de combien d'heures le four peut-il être ouvert sans risque pour les céramiques ?
Partie B
Dans cette partie, on note $t$ le temps (en heure) écoulé depuis l'instant où le four a été éteint. La température du four (en degré Celsius) à l'instant $t$ est donnée par la fonction $f$ définie, pour tout nombre réel $t$ positif, par : $$f(t) = a\text{e}^{- \frac{t}{5}} + b, $$ où $a$ et $b$ sont deux nombres réels. On admet que $f$ vérifie la relation suivante : $f'(t) + \dfrac{1}{5}f(t) = 4$.
- Déterminer les valeurs de $a$ et $b$ sachant qu'initialement, la température du four est de $ 1000 $ ° C, c'est-à-dire que $f(0) = 1000 $.
- Pour la suite, on admet que, pour tout nombre réel positif $t$: $$f(t) = 980\text{e}^{- \frac{t}{5}} + 20.$$
- Déterminer la limite de $f$ lorsque $t$ tend vers $+ \infty$.
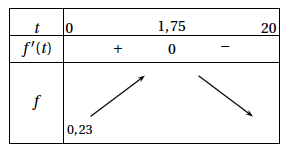
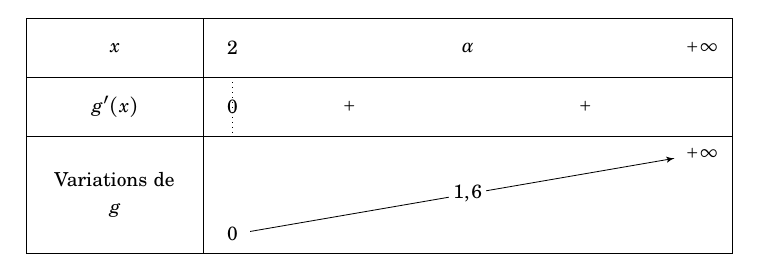
- Étudier les variations de $f$ sur $[0~;~+ \infty[$. En déduire son tableau de variations complet.
- Avec ce modèle, après combien de minutes le four peut-il être ouvert sans risque pour les céramiques ?
- La température moyenne (en degré Celsius) du four entre deux instants $t_1$ et $t_2$ est donnée par: $\dfrac{1}{t_2 - t_1}\displaystyle\int_{t_1}^{t_2} f(t)\:\text{d}t$.
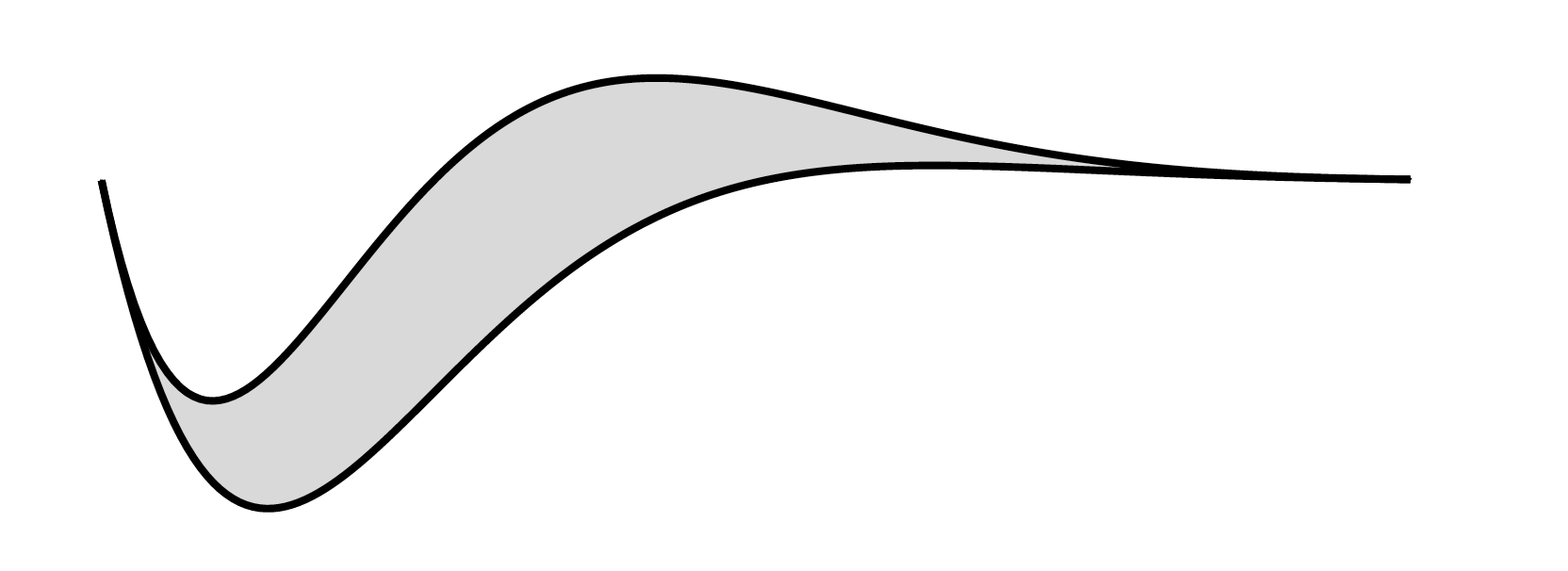
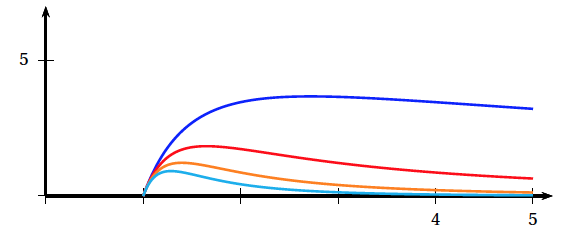
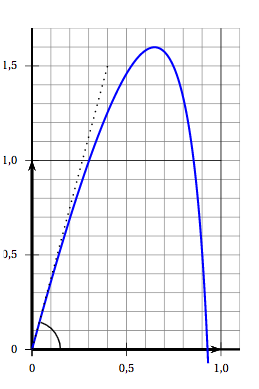
- À l'aide de la représentation graphique de $f$ ci-dessous, donner une estimation de la température moyenne $\theta$ du four sur les $15$ premières heures de refroidissement. Expliquer votre démarche.
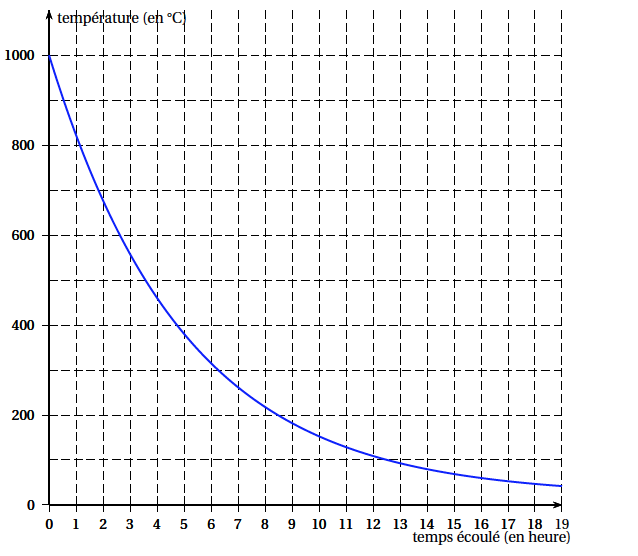
- Calculer la valeur exacte de cette température moyenne $\theta$ et en donner la valeur arrondie au degré Celsius.
- À l'aide de la représentation graphique de $f$ ci-dessous, donner une estimation de la température moyenne $\theta$ du four sur les $15$ premières heures de refroidissement. Expliquer votre démarche.
- Dans cette question, on s'intéresse à l'abaissement de température (en degré Celsius) du four au cours d'une heure, soit entre deux instants $t$ et $(t + 1)$. Cet abaissement est donné par la fonction $d$ définie, pour tout nombre réel $t$ positif, par : $d(t) = f(t) - f(t + 1)$.
- Vérifier que. pour tout nombre réel $t$ positif: $d(t) = 980\left(1 - \text{e}^{- \frac{1}{5}}\right)\text{e}^{- \frac{t}{5}}$.
- Déterminer la limite de $d(t)$ lorsque $t$ tend vers $+ \infty$. Quelle interprétation peut-on en donner ?
Correction de l'exercice 1 (5 points)
Les parties A et B peuvent être traitées de façon indépendante.
Dans une usine, un four cuit des céramiques à la température de 1000 ° C. À la fin de la cuisson, il est éteint et il refroidit.
On s'intéresse à la phase de refroidissement du four, qui débute dès l'instant où il est éteint.
La température du four est exprimée en degré Celsius ( °C).
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à $70$ °C. Sinon les céramiques peuvent se fissurer, voire se casser.
Partie A
Pour un nombre entier naturel $n$, on note $T_n$ la température en degré Celsius du four au bout de $n$ heures écoulées à partir de l'instant où il a été éteint. On a donc $T_0 = 1000 $. La température $T_n$ est calculée par l'algorithme suivant : $$ \begin{array}{|cc|}\hline T \gets 1000 \\ \text{ Pour } i \text{ allant de 1 à } n \\ \hspace{1cm} T \gets 0,82 \times T + 3,6 \\ \text{Fin Pour }\\\hline \end{array}$$
- Déterminer la température du four, arrondie à l'unité, au bout de $4$ heures de refroidissement. La variable $T$ prend successivement les valeurs suivantes (arrondies à l’unité) :
- Démontrer que, pour tout nombre entier naturel $n$, on a : $T_n = 980 \times 0,82^n + 20$. La suite $\left(T_n\right)$ est définie par $T_0=1~000$ et $T_{n+1}=0,82T_n+3,6$ pour tout entier naturel $n$.
- Au bout de combien d'heures le four peut-il être ouvert sans risque pour les céramiques ? On veut déterminer la valeur du plus petit entier naturel $n$ tel que :
$1000 \to 824 \to 679 \to 560 \to 463$
Au bout de $4$ heures de refroidissement la température du four est d’environ $463$ degré Celcius.
Montrons par récurrence que $T_n=980\times 0,82^n+20$.
Initialisation : Si $n=0$ alors $980\times 0,82^0+20=980+20=1~000=T_0$.
La propriété est vraie au rang $0$
$\quad$
Hérédité :Soit $k\geq 0$. Supposons la propriété vraie au rang $k$ : $T_n=980\times 0,82^k+20$.
Montrons qu’elle est également vraie au rang $k+1$, c’est-à-dire que $T_{k+1}=980\times 0,82^{k+1}+20$.
$\begin{align*} T_{k+1}&=0,82T_k+3,6 \\
&=0,82\left(980\times 0,82^k+20\right)+3,6 \\
&=980\times 0,82^{k+1}+16,4+3,6 \\
&=980\times 0,82^{k+1}+20
\end{align*}$
La propriété est donc vraie au rang $k+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $T_n=980\times 0,82^n+20$.
$\begin{align*} T_n\leq 70 &\iff 980\times 0,82^n+20 \leq 70 \\
&\iff 980\times 0,82^n \leq 50 \\
&\iff 0,82^n \leq \dfrac{5}{98} \\
&\iff n\ln (0,82) \leq \ln \left(\dfrac{5}{98}\right) \\
&\iff n \geq \dfrac{\ln \left(\dfrac{5}{98}\right)}{\ln (0,82)}
\end{align*}$
Or $\dfrac{\ln \left(\dfrac{5}{98}\right)}{\ln (0,82)}\approx 14,99$.
Donc le four peut être ouvert sans risque pour les céramiques au bout de $15$ heures.
Partie B
Dans cette partie, on note $t$ le temps (en heure) écoulé depuis l'instant où le four a été éteint. La température du four (en degré Celsius) à l'instant $t$ est donnée par la fonction $f$ définie, pour tout nombre réel $t$ positif, par : $$f(t) = a\text{e}^{- \frac{t}{5}} + b, $$ où $a$ et $b$ sont deux nombres réels. On admet que $f$ vérifie la relation suivante : $f'(t) + \dfrac{1}{5}f(t) = 4$.
- Déterminer les valeurs de $a$ et $b$ sachant qu'initialement, la température du four est de $ 1000 $ ° C, c'est-à-dire que $f(0) = 1000 $. On a $f(0)=1~000$ et $f(0)=a+b$ donc $a+b=1~000 \quad (1)$
- Pour la suite, on admet que, pour tout nombre réel positif $t$: $$f(t) = 980\text{e}^{- \frac{t}{5}} + 20.$$
- Déterminer la limite de $f$ lorsque $t$ tend vers $+ \infty$. $\lim\limits_{t \to +\infty} -\dfrac{t}{5}=-\infty$.
- Étudier les variations de $f$ sur $[0~;~+ \infty[$. En déduire son tableau de variations complet. On a $f'(t)=-\dfrac{980}{5}\text{e}^{-t/5}=-196\text{e}^{-t/5}$.
- Avec ce modèle, après combien de minutes le four peut-il être ouvert sans risque pour les céramiques ? On veut résoudre :
$\lim\limits_{T \to -\infty} \text{e}^T=0$
Donc $\lim\limits_{t \to +\infty} \text{e}^{-t/5}=0$
Ainsi $\lim\limits_{t \to +\infty} f(t)=20$.
$\quad$
La fonction exponentielle étant strictement positive, on a donc $f'(t)<0$ pour tout réel $t$ positif.
La fonction $f$ est donc décroissante sur $[0;+\infty[$.
On obtient ainsi le tableau de variations suivant :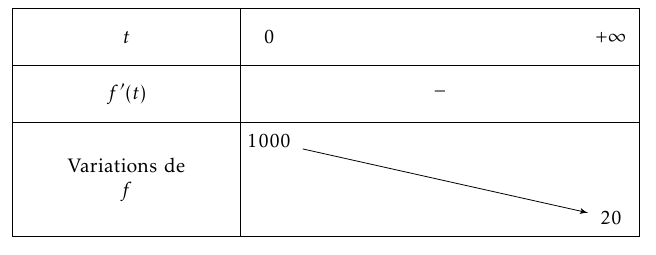
$\begin{align*} f(t)\leq 70 &\iff 980\text{e}^{-t/5}+20 \leq 70 \\
&\iff 980 \text{e}^{-t/5}\leq 50 \\
&\iff \text{e}^{-t/5} \leq \dfrac{5}{98} \\
&\iff -\dfrac{t}{5} \leq \ln \left( \dfrac{5}{98}\right) \\
&\iff t \geq -5\ln \left( \dfrac{5}{98}\right)
\end{align*}$$-5\ln \left( \dfrac{5}{98}\right) \approx 14,878$
On peut donc ouvrir le four sans risque au bout de $893$ minutes.
$\quad$ - La température moyenne (en degré Celsius) du four entre deux instants $t_1$ et $t_2$ est donnée par: $\dfrac{1}{t_2 - t_1}\displaystyle\int_{t_1}^{t_2} f(t)\:\text{d}t$.
- À l'aide de la représentation graphique de $f$ ci-dessous, donner une estimation de la température moyenne $\theta$ du four sur les $15$ premières heures de refroidissement. Expliquer votre démarche.
- Calculer la valeur exacte de cette température moyenne $\theta$ et en donner la valeur arrondie au degré Celsius.
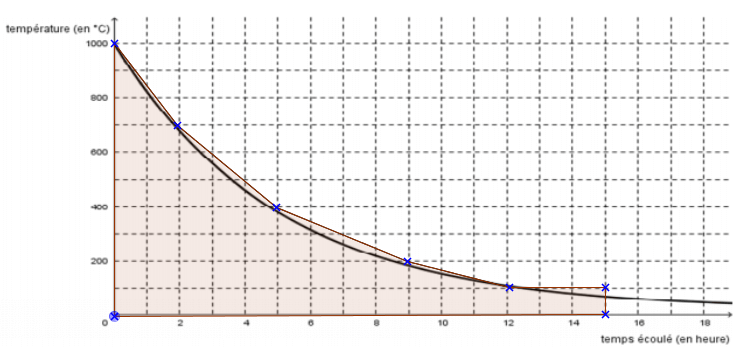
On a donc l’aire de $4$ trapèzes et celle d’un rectangle.
$\begin{align*} \mathscr{A}&=\dfrac{(1~000+700)\times 2}{2}+\dfrac{(700+400)\times 3}{2} \\
&+\dfrac{(400+200)\times 4}{2}+\dfrac{(200+100)\times 3}{2}+100\times 3 \\
&=5~300
\end{align*}$
La fonction $f$ est continue et positive sur l’intervalle $[0;15]$. L’aire du domaine compris entre la courbe représentant la fonction $f$, l’axe des abscisses et les droites d’équation $x=0$ et $x=15$ est $\displaystyle \int_0^{15}f(t)\:\text{d}t$.
Une approximation de $\displaystyle \int_0^{15}f(t) \:\text{d}t$ est $5~300$ u.a.
Ainsi une valeur approchée de la température moyenne du four sur les $15$ premières heures de refroidissement est $\theta=\dfrac{5~300}{15} \approx 353$ degré Celcius.
$\quad$
On a : - À l'aide de la représentation graphique de $f$ ci-dessous, donner une estimation de la température moyenne $\theta$ du four sur les $15$ premières heures de refroidissement. Expliquer votre démarche.
- Dans cette question, on s'intéresse à l'abaissement de température (en degré Celsius) du four au cours d'une heure, soit entre deux instants $t$ et $(t + 1)$. Cet abaissement est donné par la fonction $d$ définie, pour tout nombre réel $t$ positif, par : $d(t) = f(t) - f(t + 1)$.
- Vérifier que. pour tout nombre réel $t$ positif: $d(t) = 980\left(1 - \text{e}^{- \frac{1}{5}}\right)\text{e}^{- \frac{t}{5}}$. $\begin{align*} d(t)&=f(t)-f(t+1) \\
- Déterminer la limite de $d(t)$ lorsque $t$ tend vers $+ \infty$. Quelle interprétation peut-on en donner ? On a vu que $\lim\limits_{t \to +\infty} \text{e}^{-t/5}=0$
&=980\text{e}^{-t/5}+20-\left(980\text{e}^{-(t+1)/5}+20\right) \\
&=980\text{e}^{-t/5}-980\text{e}^{-(t+1)/5} \\
&=980\text{e}^{-t/5}\left(1-\text{e}^{-1/5}\right)
\end{align*}$
$\quad$
Donc $\lim\limits_{t \to +\infty} d(t)=0$.
Cela signifie que l’écart de température entre deux instants séparés d’une heure devient de plus en plus proche de $0$ et donc, qu’au bout d’un certain temps, la température du four se stabilise.
On sait de plus que $f'(t)+\dfrac{1}{5}f(t)=4$
Or $f'(t)=-\dfrac{a}{5}\text{e}^{-t/5}$
Donc $-\dfrac{a}{5}\text{e}^{-t/5}+\dfrac{1}{5}\left(a\text{e}^{-t/5}+b\right)=4$ pour tout réel $t$ positif.
En particulier, quand $t=0$ on a : $-\dfrac{a}{5}+\dfrac{a+b}{5}=4$
soit $-a+a+b=20 \iff b=20$
On en déduit donc, en utilisant l’équation $(1)$ que $a+20=1~000 \iff a=980$.
$\begin{align*} \theta&=\dfrac{1}{15}\displaystyle \int_0^{15} f(t)\:\text{d}t \\
&=\dfrac{1}{15}\int_0^{15} \left(980\text{e}^{-t/5}+20\right)\:\text{d}t \\
&=\dfrac{1}{15}\left[-5\times 980\text{e}^{-t/5}+20t\right]_0^{15} \\
&=\dfrac{1}{15}\left(-4~900\text{e}^{-3}+300+4~900\right) \\
&=\dfrac{5~200-4~900\text{e}^{-3}}{15} \\
&\approx 330
\end{align*}$
Exercice 2 4 points
Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$.
Les points A, B et C ont pour affixes respectives $a = - 4,\: b = 2$ et $c = 4$.
- On considère les trois points A$'$, B$'$ et C$'$ d'affixes respectives $a'= \text{j}a$, $b'= \text{j}b$ et $c'= \text{j}c$ où j est le nombre complexe $-\dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$.
- Donner la forme trigonométrique et la forme exponentielle de j. En déduire les formes algébriques et exponentielles de $a'$, $b'$ et $c'$.
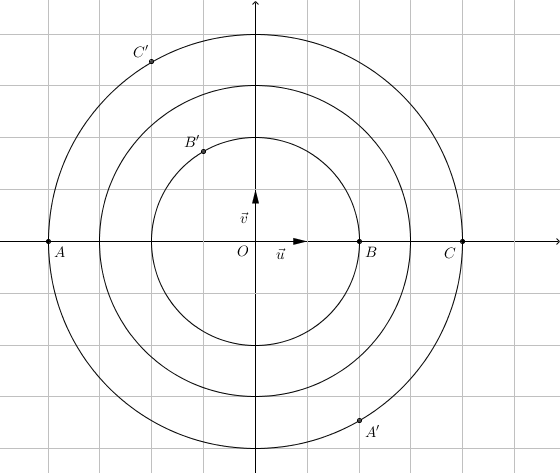
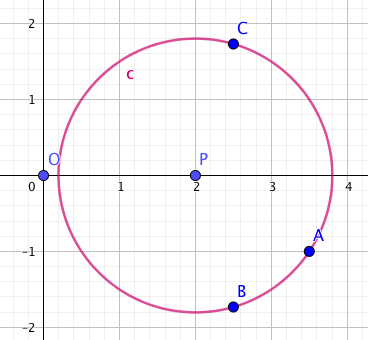
- Les points A, B et C ainsi que les cercles de centre O et de rayon 2, 3 et 4 sont représentés sur le graphique fourni ci-dessous.
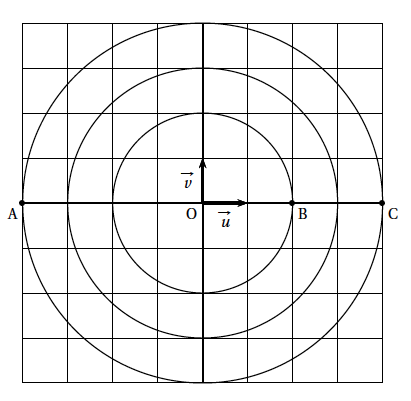
Placer les points A$'$, B$'$ et C$'$ sur ce graphique.
- Montrer que les points A$'$, B$'$ et C$'$ sont alignés.
- On note M le milieu du segment [A$'$C], N le milieu du segment [C$'$C] et P le milieu du segment [C$'$A]. Démontrer que le triangle MNP est isocèle.
Correction de l'exercice 2 (4 points)
Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$.
Les points A, B et C ont pour affixes respectives $a = - 4,\: b = 2$ et $c = 4$.
- On considère les trois points A$'$, B$'$ et C$'$ d'affixes respectives $a'= \text{j}a$, $b'= \text{j}b$ et $c'= \text{j}c$ où j est le nombre complexe $-\dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$.
- Donner la forme trigonométrique et la forme exponentielle de j. En déduire les formes algébriques et exponentielles de $a'$, $b'$ et $c'$. $|j|=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}}=1$
- Les points A, B et C ainsi que les cercles de centre O et de rayon 2, 3 et 4 sont représentés sur le graphique fourni ci-dessous.

Placer les points A$'$, B$'$ et C$'$ sur ce graphique.
$j=\cos \left(\dfrac{2\pi}{3}\right)+\sin \left(\dfrac{2\pi}{3}\right) =\text{e}^{2 \text{i}\pi/3}$.
$\quad$
Ainsi
$\begin{align*} a’&=-4j \\
&=2-2 \text{i}\sqrt{3}\quad \text{forme algébrique}\\
&=-4\text{e}^{2 \text{i} \pi/3} \\
&=4\text{e}^{2 \text{i} \pi/3+ \text{i}\pi} \\
&=4\text{e}^{5 \text{i}\pi/3} \quad \text{forme exponentielle}
\end{align*}$
$b’=-1+ \text{i}\sqrt{3}$ et $c’=-2+2 \text{i}\sqrt{3}$ $\quad$ Formes algébriques.
$b’= 2j=2\text{e}^{2 \text{i}\pi/3}$ et $c’=4j=4\text{e}^{2 \text{i}\pi/3}$ $\quad$ Formes exponentielles.
$\quad$
- Montrer que les points A$'$, B$'$ et C$'$ sont alignés. Calculons :
- On note M le milieu du segment [A$'$C], N le milieu du segment [C$'$C] et P le milieu du segment [C$'$A]. Démontrer que le triangle MNP est isocèle. L’affixe de $M$ est :
$\begin{align*} \dfrac{b’-a’}{c’-a’} &=\dfrac{2j+4j}{4j+4j} \\
&=\dfrac{6}{8} \\
&=\dfrac{3}{4}
\end{align*}$
Ainsi un argument de $\dfrac{b’-a’}{c’-a’}$ est $0$.
Les points $A’,B’$ et $C’$ sont donc alignés.
$\begin{align*} m&=\dfrac{c+a’}{2}\\
&=\dfrac{4-4j}{2}\\
&=2-2j\\
&=2+1- \text{i}\sqrt{3} \\
&=3- \text{i}\sqrt{3}
\end{align*}$.
L’affixe de $N$ est :
$\begin{align*} n&=\dfrac{c+c’}{2} \\
&=\dfrac{4+4j}{2}\\
&=2+2j\\
&=2-1+ \text{i}\sqrt{3} \\
&=1+ \text{i}\sqrt{3}\end{align*}$.
L’affixe de $P$ est :
$\begin{align*} p&=\dfrac{c’+a}{2} \\
&=\dfrac{4j-4}{2} \\
&=2j-2 \\
&=-1+ \text{i}\sqrt{3}-2 \\
&=-3+ \text{i}\sqrt{3}
\end{align*}$.
Ainsi l’affixe du vecteur $\vec{PN}$ est $z_1=1+ \text{i}\sqrt{3}-\left(-3+ \text{i}\sqrt{3}\right)=4$.
Ainsi $PN=4$
et l’affixe du vecteur $\vec{NM}$ est $z_2=3- \text{i}\sqrt{3}-\left(1+ \text{i}\sqrt{3}\right)=2-2 \text{i}\sqrt{3}$
Ainsi $NM=\sqrt{2^2+\left(2\sqrt{3}\right)^2}=4$.
Le triangle $MNP$ est donc isocèle en $N$.
Exercice 3 5 points
Une entreprise conditionne du sucre blanc provenant de deux exploitations U et V en paquets de 1 kg et de différentes qualités.
Le sucre extra fin est conditionné séparément dans des paquets portant le label « extra fin ».
Les parties A,B et C peuvent être traitées de façon indépendante.
Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième.
Partie A
Pour calibrer le sucre en fonction de la taille de ses cristaux, on le fait passer au travers d'une série de trois tamis positionnés les uns au-dessus des autres et posés sur un récipient à fond étanche. Les ouvertures des mailles sont les suivantes :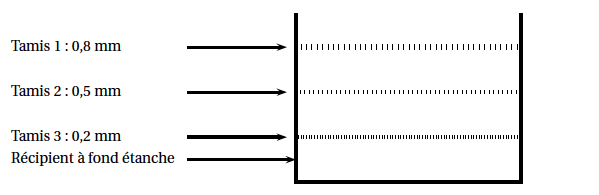
Graphique Les cristaux de sucre dont la taille est inférieure à $0,2$ mm se trouvent dans le récipient à fond étanche à la fin du calibrage. Ils seront conditionnés dans des paquets portant le label « sucre extra fin ».
- On prélève au hasard un cristal de sucre de l'exploitation U. La taille de ce cristal, exprimée en millimètre, est modélisée par la variable aléatoire $X_{\text{ U}}$ qui suit la loi normale de moyenne $\mu_{\text{ U}} = 0,58$ mm et d'écart type $\sigma_{\text{ U}} = 0,21$ mm.
- Calculer les probabilités des évènements suivants : $X_{\text{ U}} < 0,2$ et $0,5 \leqslant X_{\text{ U}} < 0,8$.
- On fait passer 1800 grammes de sucre provenant de l'exploitation U au travers de la série de tamis. Déduire de la question précédente une estimation de la masse de sucre récupérée dans le récipient à fond étanche et une estimation de la masse de sucre récupérée dans le tamis 2.
- On prélève au hasard un cristal de sucre de l'exploitation V. La taille de ce cristal, exprimée en millimètre, est modélisée par la variable aléatoire $X_{\text{V}}$ qui suit la loi normale de moyenne $\mu_{\text{V}} = 0,65$ mm et d'écart type $\sigma_{\text{V}}$ à déterminer. Lors du calibrage d'une grande quantité de cristaux de sucre provenant de l'exploitation V, on constate que 40 % de ces cristaux se retrouvent dans le tamis 2. Quelle est la valeur de l'écart type $\sigma_{\text{V}}$ de la variable aléatoire $X_{\text{V}}$ ?
Partie B
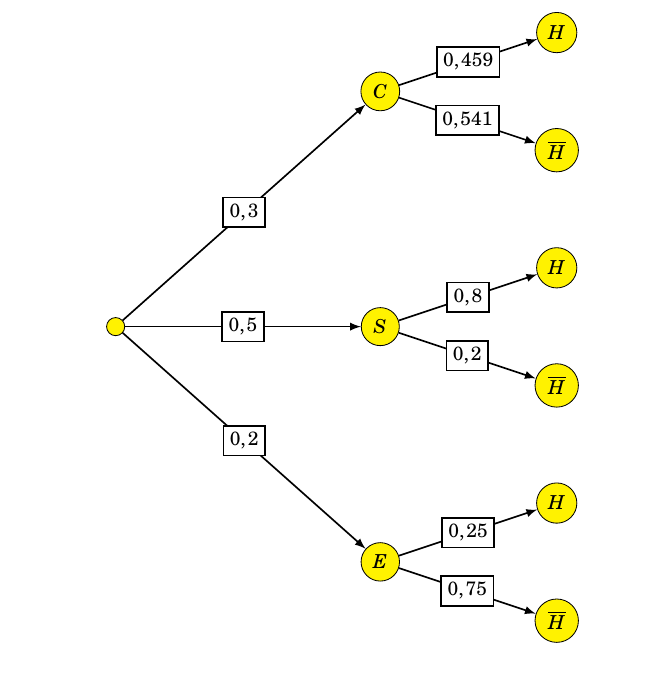
Dans cette partie, on admet que 3 % du sucre provenant de l'exploitation U est extra fin et que 5 % du sucre provenant de l'exploitation V est extra fin. On prélève au hasard un paquet de sucre dans la production de l'entreprise et, dans un souci de traçabilité, on s'intéresse à la provenance de ce paquet. On considère les évènements suivants:- $U$ : « Le paquet contient du sucre provenant de l'exploitation U » ;
- $V$ : «Le paquet contient du sucre provenant de l'exploitation V » ;
- $E$ : «Le paquet porte le label "extra fin" ».
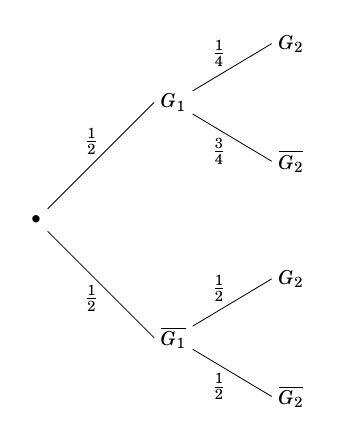
- Dans cette question, on admet que l'entreprise fabrique 30 % de ses paquets avec du sucre provenant de l'exploitation U et les autres avec du sucre provenant de l'exploitation V, sans mélanger les sucres des deux exploitations.
- Quelle est la probabilité que le paquet prélevé porte le label «extra fin » ?
- Sachant qu'un paquet porte le label «extra fin », quelle est la probabilité que le sucre qu'il contient provienne de l'exploitation U ?
- L'entreprise souhaite modifier son approvisionnement auprès des deux exploitations afin que parmi les paquets portant le label « extra fin », 30 % d'entre eux contiennent du sucre provenant de l'exploitation U. Comment doit-elle s'approvisionner auprès des exploitations U et V ?
Toute trace de recherche sera valorisée dans cette question.Partie C
- L'entreprise annonce que 30 % des paquets de sucre portant le label «extra fin» qu'elle conditionne contiennent du sucre provenant de l'exploitation U. Avant de valider une commande, un acheteur veut vérifier cette proportion annoncée. Il prélève $150$ paquets pris au hasard dans la production de paquets labellisés «extra fin » de l'entreprise. Parmi ces paquets, $30$ contiennent du sucre provenant de l'exploitation U. A-t-il des raisons de remettre en question l'annonce de l'entreprise ?
- L'année suivante, l'entreprise déclare avoir modifié sa production. L'acheteur souhaite estimer la nouvelle proportion de paquets de sucre provenant de l'exploitation U parmi les paquets portant le label «extra fin » . Il prélève 150 paquets pris au hasard dans la production de paquets labellisés «extra fin » de l'entreprise. Parmi ces paquets 42 % contiennent du sucre provenant de l'exploitation U. Donner un intervalle de confiance, au niveau de confiance 95 %, de la nouvelle proportion de paquets labellisés «extra fin » contenant du sucre provenant de l'exploitation U.
Correction de l'exercice 3 (5 points)
Une entreprise conditionne du sucre blanc provenant de deux exploitations U et V en paquets de 1 kg et de différentes qualités.
Le sucre extra fin est conditionné séparément dans des paquets portant le label « extra fin ».
Les parties A,B et C peuvent être traitées de façon indépendante.
Dans tout l'exercice, les résultats seront arrondis, si nécessaire, au millième.Partie A
Pour calibrer le sucre en fonction de la taille de ses cristaux, on le fait passer au travers d'une série de trois tamis positionnés les uns au-dessus des autres et posés sur un récipient à fond étanche. Les ouvertures des mailles sont les suivantes :
Graphique Les cristaux de sucre dont la taille est inférieure à $0,2$ mm se trouvent dans le récipient à fond étanche à la fin du calibrage. Ils seront conditionnés dans des paquets portant le label « sucre extra fin ».- On prélève au hasard un cristal de sucre de l'exploitation U. La taille de ce cristal, exprimée en millimètre, est modélisée par la variable aléatoire $X_{\text{ U}}$ qui suit la loi normale de moyenne $\mu_{\text{ U}} = 0,58$ mm et d'écart type $\sigma_{\text{ U}} = 0,21$ mm.
- Calculer les probabilités des évènements suivants : $X_{\text{ U}} < 0,2$ et $0,5 \leqslant X_{\text{ U}} < 0,8$. On a, à l’aide de la calculatrice :
- On fait passer 1800 grammes de sucre provenant de l'exploitation U au travers de la série de tamis. Déduire de la question précédente une estimation de la masse de sucre récupérée dans le récipient à fond étanche et une estimation de la masse de sucre récupérée dans le tamis 2. Dans le récipient à fond étanche on récupère les cristaux de sucre dont la taille est inférieure à $0,2$ mm et dans le tamis 2 les cristaux de sucre dont la taille est comprise entre $0,5$ et $0,8$ mm.
$P\left(X_U<0,2\right)=0,5-P\left(0,2<X_U<0,58\right) \approx 0,035$
$P\left(0,5 \leq X_U<0,8\right) \approx 0,501$
$\quad$
D’après la question précédente on récupère :
$\bullet$ $0,035\times 1~800=63$ g de sucre dans le récipient à fond étanche;
$\bullet$ $0,501\times 1~800=901,8$ g de sucre dans le tamis 2. - On prélève au hasard un cristal de sucre de l'exploitation V. La taille de ce cristal, exprimée en millimètre, est modélisée par la variable aléatoire $X_{\text{V}}$ qui suit la loi normale de moyenne $\mu_{\text{V}} = 0,65$ mm et d'écart type $\sigma_{\text{V}}$ à déterminer. Lors du calibrage d'une grande quantité de cristaux de sucre provenant de l'exploitation V, on constate que 40 % de ces cristaux se retrouvent dans le tamis 2. Quelle est la valeur de l'écart type $\sigma_{\text{V}}$ de la variable aléatoire $X_{\text{V}}$ ? La variable aléatoire $X=\dfrac{X_V-0,65}{\sigma_V}$ suit la loi normale centrée réduite.
On sait que :
$\begin{align*} P\left(0,5 \leq X_V < 0,8\right)=0,4 &\iff P\left(-0,15\leq X_V-0,65< 0,15\right)=0,4 \\
&\iff P\left(-\dfrac{0,15}{\sigma_V} \leq X < \dfrac{0,15}{\sigma_V}\right) =0,4 \\
&\iff 2P\left(X<\dfrac{0,15}{\sigma_V}\right)-1=0,4 \\
&\iff 2P\left(X<\dfrac{0,15}{\sigma_V}\right)=1,4 \\
&\iff P\left(X<\dfrac{0,15}{\sigma_V}\right)=0,7
\end{align*}$
À l’aide de la fonction inverse loi normale de la calculatrice on trouve $\dfrac{0,15}{\sigma_V}\approx 0,524$
Donc $\sigma_V \approx 0,286$.
Partie B
Dans cette partie, on admet que 3 % du sucre provenant de l'exploitation U est extra fin et que 5 % du sucre provenant de l'exploitation V est extra fin. On prélève au hasard un paquet de sucre dans la production de l'entreprise et, dans un souci de traçabilité, on s'intéresse à la provenance de ce paquet. On considère les évènements suivants:- $U$ : « Le paquet contient du sucre provenant de l'exploitation U » ;
- $V$ : «Le paquet contient du sucre provenant de l'exploitation V » ;
- $E$ : «Le paquet porte le label "extra fin" ».
- Dans cette question, on admet que l'entreprise fabrique 30 % de ses paquets avec du sucre provenant de l'exploitation U et les autres avec du sucre provenant de l'exploitation V, sans mélanger les sucres des deux exploitations.
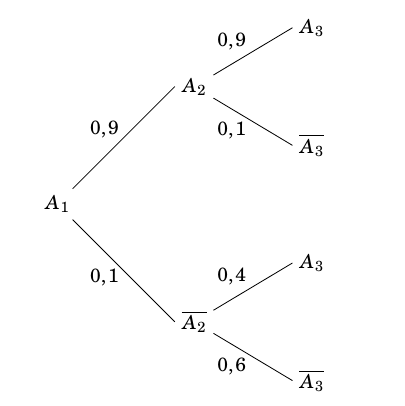
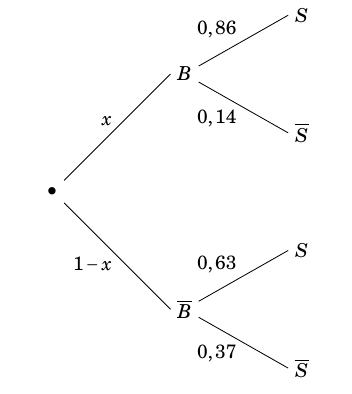
- Quelle est la probabilité que le paquet prélevé porte le label «extra fin » ? On a $p(U)=0,3$, $p(V)=0,7$, $p_U(E)=0,03$ et $p_V(E)=0,05$.
- Sachant qu'un paquet porte le label «extra fin », quelle est la probabilité que le sucre qu'il contient provienne de l'exploitation U ? On veut calculer :
D’après la formule des probabilités totales on a:
$\begin{align*} p(E)&=p(U\cap E)+p(V\cap E) \\
&=0,3\times 0,03+0,7\times 0,05 \\
&=0,044
\end{align*}$
La probabilité que le paquet prélevé porte le label “extra fin” est $0,044$.
$\begin{align*} p_E(U)&=\dfrac{p(E\cap U)}{p(E)} \\
&=\dfrac{0,3\times 0,03}{0,044} \\
&=\dfrac{9}{44}
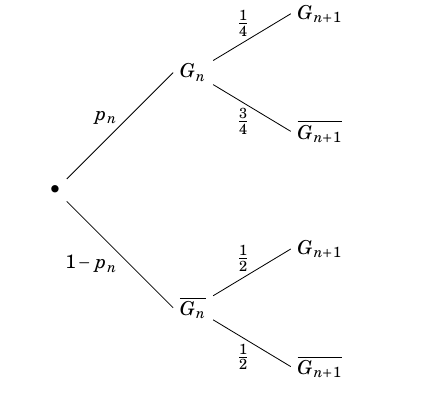
\end{align*}$ - L'entreprise souhaite modifier son approvisionnement auprès des deux exploitations afin que parmi les paquets portant le label « extra fin », 30 % d'entre eux contiennent du sucre provenant de l'exploitation U. Comment doit-elle s'approvisionner auprès des exploitations U et V ? Soit $x$ un réel appartenant à $[0;1]$.
On a $p(U)=x$, $p(V)=1-x$, $p_U(E)=0,03$ et $p_V(E)=0,05$.
D’après la formule des probabilités totales on a:
$\begin{align*} p(E)&=p(U\cap E)+p(V\cap E) \\
&=0,03x+0,05(1-x) \\
&=0,05-0,02x
\end{align*}$
On sait que :
$\begin{align*} p_E(U)=0,3 &\iff \dfrac{p(E\cap U)}{p(E)} =0,3\\
&\iff \dfrac{0,03x}{0,05-0,02x}=0,3 \\
&\iff 0,03x=0,015-0,006x \\
&\iff 0,036x=0,015 \\
&\iff x=\dfrac{5}{12}
\end{align*}$
Il faut donc que que $p(U)=\dfrac{5}{12}$ et $p(V)=\dfrac{7}{12}$
$\quad$
Toute trace de recherche sera valorisée dans cette question.Partie C
- L'entreprise annonce que 30 % des paquets de sucre portant le label «extra fin» qu'elle conditionne contiennent du sucre provenant de l'exploitation U. Avant de valider une commande, un acheteur veut vérifier cette proportion annoncée. Il prélève $150$ paquets pris au hasard dans la production de paquets labellisés «extra fin » de l'entreprise. Parmi ces paquets, $30$ contiennent du sucre provenant de l'exploitation U. A-t-il des raisons de remettre en question l'annonce de l'entreprise ? On a $n=150$ et $p=0,3$.
- L'année suivante, l'entreprise déclare avoir modifié sa production. L'acheteur souhaite estimer la nouvelle proportion de paquets de sucre provenant de l'exploitation U parmi les paquets portant le label «extra fin » . Il prélève 150 paquets pris au hasard dans la production de paquets labellisés «extra fin » de l'entreprise. Parmi ces paquets 42 % contiennent du sucre provenant de l'exploitation U. Donner un intervalle de confiance, au niveau de confiance 95 %, de la nouvelle proportion de paquets labellisés «extra fin » contenant du sucre provenant de l'exploitation U. On a $n=150$ et $f=0,42$
Donc $n=150 \geq 30$, $np=45 \geq 5$ et $n(1-p)=105\geq 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$\begin{align*} I_{150}&=\left[0,3-1,96\sqrt{\dfrac{0,3\times 0,7}{150}};0,3+1,96\sqrt{\dfrac{0,3\times 0,7}{150}}\right] \\
&\approx [0,226;0,374]
\end{align*}$
La fréquence observée est $f=\dfrac{30}{150}=0,2 \notin I_{150}$.
Au risque d’erreur de $5\%$, il a donc raison de remettre en question l’annonce de l’entreprise.
$\quad$
Donc $n=150\geq 30$, $nf=63\geq 5$ et $n(1-f)=87\geq 5$.
Un intervalle de confiance au niveau de confiance $95\%$ est :
$\begin{align*} J_{150}&=\left[0,42-\dfrac{1}{\sqrt{150}};0,42+\dfrac{1}{\sqrt{150}}\right] \\
&\approx [0,338;0,502]
\end{align*}$
Exercice 4 5 points
Dans l'espace muni du repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives $(2~;~1~;~4)$, $(4~;~-1~;~0)$, $(0~;~3~;~2)$ et $(4~;~3~;~-2)$.
- Déterminer une représentation paramétrique de la droite (CD).
- Soit $M$ un point de la droite (CD).
- Déterminer les coordonnées du point $M$ tel que la distance B$M$ soit minimale.
- On note H le point de la droite (CD) ayant pour coordonnées $(3~;~3~;~- 1)$. Vérifier que les droites (BH) et (CD) sont perpendiculaires.
- Montrer que l'aire du triangle BCD est égale à 12 cm$^2$.
-
- Démontrer que le vecteur $\vec{n}\begin{pmatrix}2\\1\\2\end{pmatrix}$ est un vecteur normal au plan (BCD).
- Déterminer une équation cartésienne du plan (BCD).
- Déterminer une représentation paramétrique de la droite $\Delta$ passant par A et orthogonale au plan (BCD).
- Démontrer que le point I, intersection de la droite $\Delta$ et du plan (BCD) a pour coordonnées $\left(\dfrac{2}{3}~;~\dfrac{1}{3}~;~\dfrac{8}{3}\right)$.
- Calculer le volume du tétraèdre ABCD.
Correction de l'exercice 4 5 points
Dans l'espace muni du repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives $(2~;~1~;~4)$, $(4~;~-1~;~0)$, $(0~;~3~;~2)$ et $(4~;~3~;~-2)$.
- Déterminer une représentation paramétrique de la droite (CD). On a $\vec{CD}(4;0;-4)$.
- Soit $M$ un point de la droite (CD).
- Déterminer les coordonnées du point $M$ tel que la distance B$M$ soit minimale. On a donc $M(4t;3;2-4t)$
- On note H le point de la droite (CD) ayant pour coordonnées $(3~;~3~;~- 1)$. Vérifier que les droites (BH) et (CD) sont perpendiculaires. On a $\vec{BH}(-1;4;-1)$ et $\vec{CD}(4;0;-4)$.
- Montrer que l'aire du triangle BCD est égale à 12 cm$^2$. On a $CD=\sqrt{4^2+(-4)^2}=\sqrt{32}=4\sqrt{2}$
Ainsi
$\begin{align*} BM&=\sqrt{(4t-4)^2+(3+1)^2+(2-4t)^2} \\
&=\sqrt{16t^2-32t+16+16+4-16t+16t^2} \\
&=\sqrt{32t^2-48t+36}
\end{align*}$
La fonction racine carrée étant strictement croissante sur l’intervalle $[0;+\infty[$, $BM$ est minimal quand $32t^2-48t+36$ l’est aussi.
Le coefficient principal de cette expression du second degré est $a=32>0$.
L’expression possède donc un minimum en $t_0=-\dfrac{b}{2a}=\dfrac{48}{64}=0,75$.
Ainsi la distance $BM$ est minimale pour $M(3;3;-1)$.
$\quad$
Par conséquent $\vec{BH}.\vec{CD}=-1\times 4+0+(-1)\times (-4)=0$.
Les vecteurs sont donc orthogonaux et les droites $(BH)$ et $(CD)$sont perpendiculaires (elles ont un point d’intersection puisque le point $H$ appartient à chacune d’entre-elles).
$\quad$
et $BH=\sqrt{(-1)^2+4^2+(-1)^2}=\sqrt{18}=3\sqrt{2}$
L’aire du triangle $BCD$ est $\dfrac{CD\times BH}{2}=\dfrac{4\sqrt{2}\times 3\sqrt{2}}{2}=12$ cm$^2$.
$\quad$ -
- Démontrer que le vecteur $\vec{n}\begin{pmatrix}2\\1\\2\end{pmatrix}$ est un vecteur normal au plan (BCD). On a $\vec{BC}(-4;4;2)$.
- Déterminer une équation cartésienne du plan (BCD). Une équation cartésienne du plan $(BCD)$ est donc de la forme :
- Déterminer une représentation paramétrique de la droite $\Delta$ passant par A et orthogonale au plan (BCD). La droite $\Delta$ est orthogonale au plan $(BCD)$.
- Démontrer que le point I, intersection de la droite $\Delta$ et du plan (BCD) a pour coordonnées $\left(\dfrac{2}{3}~;~\dfrac{1}{3}~;~\dfrac{8}{3}\right)$. Montrons que le point $I$ appartient au plan $(BCD)$.
- Calculer le volume du tétraèdre ABCD. On a $AI=\sqrt{\left(\dfrac{2}{3}-2\right)^2+\left(\dfrac{1}{3}-1\right)^2+\left(\dfrac{8}{3}-4\right)^2}=2$
Donc $\vec{BC}.\vec{n}=-4\times 2+4\times 1+2\times 2=-8+4+4=0$
et $\vec{CD}.\vec{n}=4\times 2+0-4\times 2=0$
Les vecteurs $\vec{CD}$ et $\vec{BC}$ sont clairement non colinéaires (une coordonnée est nulle pour l’un et pour l’autre).
Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(BCD)$.
Il est donc normal au plan $(BCD)$.
$\quad$
$2x+y+2z+d=0$
Le point $C(0;3;2)$ appartient au plan.
Par conséquent $3+4+d=0 \iff d=-7$.
Une équation cartésienne du plan $(BCD)$ est donc $2x+y+2z-7=0$.
$\quad$
$\vec{n}$ est donc un vecteur directeur de cette droite.
Ainsi une représentation paramétrique de la droite $\Delta$ est :
$\begin{cases} x=2+2k\\y=1+k\\z=4+2k\end{cases} \quad, k\in \mathbb{R}$.
$\quad$
$2\times \dfrac{2}{3}+\dfrac{1}{3}+2\times \dfrac{8}{3}-7=\dfrac{4}{3}+\dfrac{1}{3}+\dfrac{16}{3}-7=\dfrac{21}{3}-7=0$
Ainsi $I\in (BCD)$.
$\quad$
Montrons que le point $I$ appartient à la droite $\Delta$.
On doit donc résoudre le système
$\begin{cases} 2+2k=\dfrac{2}{3}\\1+k=\dfrac{1}{3}\\4+2k=\dfrac{8}{3}\end{cases} \iff k=-\dfrac{2}{3}$
Donc $I\in \Delta$.
Le point $I$ est par conséquent le point d’intersection de la droite $\Delta$ et du plan $(BCD)$.
$\quad$
Par conséquent le volume du tétraèdre $ABCD$ est :
$V=\dfrac{AI\times \mathscr{A}_{BCD}}{3}=\dfrac{2\times 12}{3}=8$ cm$^3$.
Une représentation paramétrique de la droite $(CD)$ est donc $\begin{cases} x=4t\\y=3\\z=2-4t\end{cases} \quad, t\in\mathbb{R}$.
$\quad$
Spécialité 5 points
À toute lettre de l'alphabet on associe un nombre entier $x$ compris entre 0 et 25 comme indiqué dans le tableau ci-dessous: $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \text{Lettre } &A &B &C &D &E &F &G &H &I &J &K &L &M\\ \hline x &0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\ \hline\hline \text{Lettre } &N &O &P &Q &R &S &T &U &V &W &X &Y &Z\\ \hline x &13&14&15&16&17&18&19&20&21&22&23 &24 &25\\ \hline \end{array}$$
Le «chiffre de RABIN » est un dispositif de cryptage asymétrique inventé en 1979 par l'informaticien Michael Rabin.
Alice veut communiquer de manière sécurisée en utilisant ce cryptosystème. Elle choisit deux nombres premiers distincts $p$ et $q$. Ce couple de nombres est sa clé privée qu'elle garde secrète. Elle calcule ensuite $n = p \times q$ et elle choisit un nombre entier naturel $B$ tel que $0 \leqslant B \leqslant n -1$. Si Bob veut envoyer un message secret à Alice, il le code lettre par lettre. Le codage d'une lettre représentée par le nombre entier $x$ est le nombre $y$ tel que : \[y \equiv x(x + B)\:\: [n] \:\text{ avec }\: 0 \leqslant y \leqslant n.\] Dans tout l'exercice on prend $p = 3,\: q = 11$ donc $n = p \times q = 33$ et $B = 13$.
Partie A : Cryptage
Bob veut envoyer le mot « NO » à Alice.
- Montrer que Bob code la lettre «N » avec le nombre 8.
- Déterminer le nombre qui code la lettre «O ».
Partie B : Décryptage
Alice a reçu un message crypté qui commence par le nombre 3. Pour décoder ce premier nombre, elle doit déterminer le nombre entier $x$ tel que : \[x(x + 13) \equiv 3 \:\: [33]\: \text{ avec }\: 0 \leqslant x < 26.\]
- Montrer que $x(x + 13) \equiv 3\:\: [33]$ équivaut à $(x + 23)^2 \equiv 4\:\: [33]$.
-
- Montrer que si $(x + 23)^2 \equiv 4\:\: [33]$ alors le système d'équations $\left\{\begin{array}{l c l} (x + 23)^2 &\equiv &4 \:\: [3]\\ (x + 23)^2 &\equiv &4 \:\: [11] \end{array}\right.$ est vérifié.
- Réciproquement, montrer que si $\left\{\begin{array}{l c l} (x + 23)^2 &\equiv &4\:\: [3]\\ (x + 23)^2 &\equiv &4 \:\: [11] \end{array}\right.$ alors $(x + 23)^2 \equiv 4\:\: [33]$.
- En déduire que $x(x + 13) \equiv 3\:\: [33] \iff \left\{\begin{array}{l c l} (x + 23)^2 &\equiv&1 \:\: [3]\\ (x + 23)^2 &\equiv& 4 \:\: [11] \end{array}\right.$
-
- Déterminer les nombres entiers naturels $a$ tels que $0 \leqslant a < 3$ et $a^2 \equiv 1 \:\: [3]$.
- Déterminer les nombres entiers naturels $b$ tels que $0 \leqslant b < 11$ et $b^2 \equiv 4\:\: [11]$.
-
- En déduire que $x(x + 13) \equiv 3 \quad[33]$ équivaut aux quatre systèmes suivants : \[\left\{\begin{array}{l c l} x &\equiv&2\quad [3]\\ x&\equiv &8\quad[11] \end{array}\right. \: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 0\quad[3]\\ x &\equiv& 1 \quad[11] \end{array}\right.\: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 2\quad[3]\\ x &\equiv&1 \quad[11] \end{array}\right.\: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 0\quad [3]\\ x &\equiv& 8 \quad [11] \end{array}\right.\]
- On admet que chacun de ces systèmes admet une unique solution entière $x$ telle que $0 \leqslant x < 33$. Déterminer, sans justification, chacune de ces solutions.
- Compléter l'algorithme en Annexe pour qu'il affiche les quatre solutions trouvées dans la question précédente.
- Alice peut-elle connaître la première lettre du message envoyé par Bob ? Le «chiffre de RABIN » est-il utilisable pour décoder un message lettre par lettre ?
Annexe

Correction de l'exercice de Spécialité 5 points
À toute lettre de l'alphabet on associe un nombre entier $x$ compris entre 0 et 25 comme indiqué dans le tableau ci-dessous: $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \text{Lettre } &A &B &C &D &E &F &G &H &I &J &K &L &M\\ \hline x &0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12\\ \hline\hline \text{Lettre } &N &O &P &Q &R &S &T &U &V &W &X &Y &Z\\ \hline x &13&14&15&16&17&18&19&20&21&22&23 &24 &25\\ \hline \end{array}$$
Le «chiffre de RABIN » est un dispositif de cryptage asymétrique inventé en 1979 par l'informaticien Michael Rabin.
Alice veut communiquer de manière sécurisée en utilisant ce cryptosystème. Elle choisit deux nombres premiers distincts $p$ et $q$. Ce couple de nombres est sa clé privée qu'elle garde secrète. Elle calcule ensuite $n = p \times q$ et elle choisit un nombre entier naturel $B$ tel que $0 \leqslant B \leqslant n -1$. Si Bob veut envoyer un message secret à Alice, il le code lettre par lettre. Le codage d'une lettre représentée par le nombre entier $x$ est le nombre $y$ tel que : \[y \equiv x(x + B)\:\: [n] \:\text{ avec }\: 0 \leqslant y \leqslant n.\] Dans tout l'exercice on prend $p = 3,\: q = 11$ donc $n = p \times q = 33$ et $B = 13$.
Partie A : Cryptage
Bob veut envoyer le mot « NO » à Alice.
- Montrer que Bob code la lettre «N » avec le nombre 8. $N$ est associé au nombre $x=13$.
- Déterminer le nombre qui code la lettre «O ». $O$ est associé au nombre $x=14$.
Ainsi $y \equiv 13(13+13) ~~[33] \equiv 338~~[33]\equiv 8~~[33]$.
Donc Bob code la lettre $N$ avec le nombre $8$.
Ainsi $y \equiv 14(14+13) ~~[33] \equiv 378~~[33]\equiv 15~~[33]$.
Donc Bob code la lettre $O$ avec le nombre $15$.
$\quad$
Partie B : Décryptage
Alice a reçu un message crypté qui commence par le nombre 3. Pour décoder ce premier nombre, elle doit déterminer le nombre entier $x$ tel que : \[x(x + 13) \equiv 3 \:\: [33]\: \text{ avec }\: 0 \leqslant x < 26.\]
- Montrer que $x(x + 13) \equiv 3\:\: [33]$ équivaut à $(x + 23)^2 \equiv 4\:\: [33]$. On a :
-
- Montrer que si $(x + 23)^2 \equiv 4\:\: [33]$ alors le système d'équations $\left\{\begin{array}{l c l} (x + 23)^2 &\equiv &4 \:\: [3]\\ (x + 23)^2 &\equiv &4 \:\: [11] \end{array}\right.$ est vérifié. Si $(x+23)^2\equiv 4~~[33]$ alors il existe un entier relatif $k$ tel que : $(x+23)^2=4+33k $
- Réciproquement, montrer que si $\left\{\begin{array}{l c l} (x + 23)^2 &\equiv &4\:\: [3]\\ (x + 23)^2 &\equiv &4 \:\: [11] \end{array}\right.$ alors $(x + 23)^2 \equiv 4\:\: [33]$. Si le système $\begin{cases} (x+23)^2\equiv 4~~[3]\\(x+23)^2\equiv 4~~[11]\end{cases}$ est vérifié alors il existe deux entiers relatifs $k$ et $k’$ tels que
- En déduire que $x(x + 13) \equiv 3\:\: [33] \iff \left\{\begin{array}{l c l} (x + 23)^2 &\equiv&1 \:\: [3]\\ (x + 23)^2 &\equiv& 4 \:\: [11] \end{array}\right.$ On a donc :
Or $(x+23)^2=4+33k \iff (x+23)^2=4+11k\times 3$
Donc $(x+23)^2\equiv 4~~[3]$
De plus $(x+23)^2=4+33k \iff (x+23)^2=4+3k\times 11$
Donc $(x+23)^2\equiv 4~~[11]$
Par conséquent le système $\begin{cases} (x+23)^2\equiv 4~~[3]\\(x+23)^2\equiv 4~~[11]\end{cases}$ est vérifié.
$\quad$
$(x+23)^2=4+3k$ et $(x+23)^2=4+11k’$.
Par conséquent $4+3k=4+11k’ \iff 3k=11k’$.
Les nombres $3$ et $11$ sont premiers entre-eux.
D’après le théorème de Gauss cela signifie donc que $3$ divise $k’$.
Par conséquent, il existe un entier relatif $q$ tel que $k’=3q$.
Ainsi $(x+23)^2=4+11\times 3q=4+33q$.
Donc $(x+23)^2\equiv 4~~[33]$.
$\quad$
$\begin{align*} x(x+13)\equiv 3~~[33]&\iff (x+23)^2\equiv 4~~[33] \\
&\iff \begin{cases} (x+23)^2\equiv 4~~[3]\\(x+23)^2\equiv 4~~[11]\end{cases}
&\iff \begin{cases} (x+23)^2\equiv 1~~[3]\\(x+23)^2\equiv 4~~[11]\end{cases}
\end{align*}$ -
- Déterminer les nombres entiers naturels $a$ tels que $0 \leqslant a < 3$ et $a^2 \equiv 1 \:\: [3]$. $0^2=0 \equiv 0~~[3]$
- Déterminer les nombres entiers naturels $b$ tels que $0 \leqslant b < 11$ et $b^2 \equiv 4\:\: [11]$. $0^2=0\equiv 0~~[11]$
$1^1=1\equiv 1~~[3]$
$2^2=4\equiv 1~~[3]$
Donc les entiers naturels vérifiant $0\leq a<3$ et $a^2\equiv 1~~[3]$ sont $1$ et $2$.
$1^2=1\equiv 1~~[11]$
$2^2=4\equiv 4~~[11]$
$3^2=8\equiv 9~~[11]$
$4^2=16\equiv 5~~[11]$
$5^2=25\equiv 3~~[11]$
$6^2=36\equiv 3~~[11]$
$7^2=49\equiv 5~~[11]$
$8^2=64\equiv 9~~[11]$
$9^2=81\equiv 4~~[11]$
$10^2=100\equiv 1~~[11]$
Donc les entiers naturels vérifiant $0\leq b<11$ et $b^2\equiv 4~~[11]$ sont $2$ et $9$.
$\quad$ -
- En déduire que $x(x + 13) \equiv 3 \quad[33]$ équivaut aux quatre systèmes suivants : \[\left\{\begin{array}{l c l} x &\equiv&2\quad [3]\\ x&\equiv &8\quad[11] \end{array}\right. \: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 0\quad[3]\\ x &\equiv& 1 \quad[11] \end{array}\right.\: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 2\quad[3]\\ x &\equiv&1 \quad[11] \end{array}\right.\: \text{ ou } \left\{\begin{array}{l c l} x &\equiv& 0\quad [3]\\ x &\equiv& 8 \quad [11] \end{array}\right.\] Ainsi $x(x+13)\equiv 3~~[33]$ équivaut à
- On admet que chacun de ces systèmes admet une unique solution entière $x$ telle que $0 \leqslant x < 33$. Déterminer, sans justification, chacune de ces solutions. Si $0\leq x <33$
$\begin{cases} x+23\equiv 1~~[3]\\x+23\equiv 2~~[11]\end{cases}$ ou $\begin{cases} x+23\equiv 2~~[3]\\x+23\equiv 2~~[11]\end{cases}$ ou $\begin{cases} x+23\equiv 1~~[3]\\x+23\equiv 9~~[11]\end{cases}$ ou $\begin{cases} x+23\equiv 2~~[3]\\x+23\equiv 9~~[11]\end{cases}$
Ce qui équivaut à
$\begin{cases} x\equiv -22~~[3]\\x\equiv -21~~[11]\end{cases}$ ou $\begin{cases} x\equiv -21~~[3]\\x\equiv -21~~[11]\end{cases}$ ou $\begin{cases} x\equiv -22~~[3]\\x\equiv -14~~[11]\end{cases}$ ou $\begin{cases} x\equiv -21~~[3]\\x\equiv -14~~[11]\end{cases}$
Ce qui équivaut à
$\begin{cases} x\equiv 2~~[3]\\x\equiv 1~~[11]\end{cases}$ ou $\begin{cases} x\equiv 0~~[3]\\x\equiv 1~~[11]\end{cases}$ ou $\begin{cases} x\equiv 2~~[3]\\x\equiv 8~~[11]\end{cases}$ ou $\begin{cases} x\equiv 0~~[3]\\x\equiv 8~~[11]\end{cases}$
$\quad$
Alors :
– une solution de $\begin{cases} x\equiv 2~~[3]\\x\equiv 8~~[11]\end{cases}$ est $8$.
– une solution de $\begin{cases} x\equiv 0~~[3]\\x\equiv 1~~[11]\end{cases}$ est $12$.
– une solution de $\begin{cases} x\equiv 2~~[3]\\x\equiv 1~~[11]\end{cases}$ est $23$.
– une solution de $\begin{cases} x\equiv 0~~[3]\\x\equiv 8~~[11]\end{cases}$ est $30$. - Compléter l'algorithme en Annexe pour qu'il affiche les quatre solutions trouvées dans la question précédente.
- Alice peut-elle connaître la première lettre du message envoyé par Bob ? Le «chiffre de RABIN » est-il utilisable pour décoder un message lettre par lettre ? Pour le nombre $3$ possède il existe $4$ valeurs de $x$ possibles.
$\begin{align*} (x+23)^2\equiv 4~~[33] &\iff x^2+46x+529 \equiv 4 ~~[33] \\
&\iff x^2+46x\equiv -525~~[33] \\
&\iff x^2+13x\equiv 3~~[33] \\
&\iff x(x+13)\equiv 3~~[33]\\
\end{align*}$
$\quad$
Annexe
 On obtient l’algorithme suivant :
On obtient l’algorithme suivant :Pour $x$ allant de $0$ à $32$
$\quad$ Si le reste de la division de $x(x+13)$ par $33$ est égal à $3$ alors
$\qquad$ Afficher $x$
$\quad$ Fin Si
Fin Pour
$\quad$
Le “chiffre de RABIN” n’est donc pas utilisable pour décoder un message lettre par lettre.
- Vues: 30482


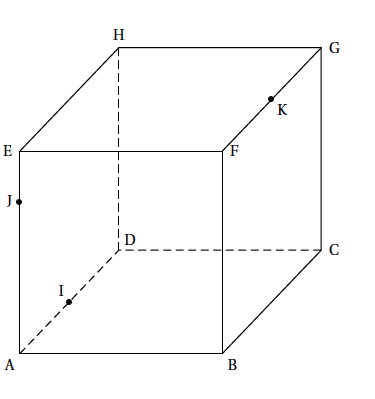
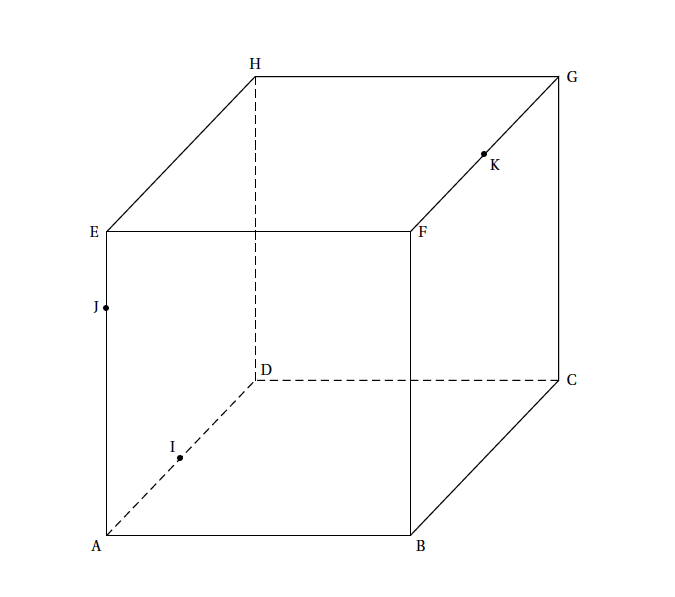
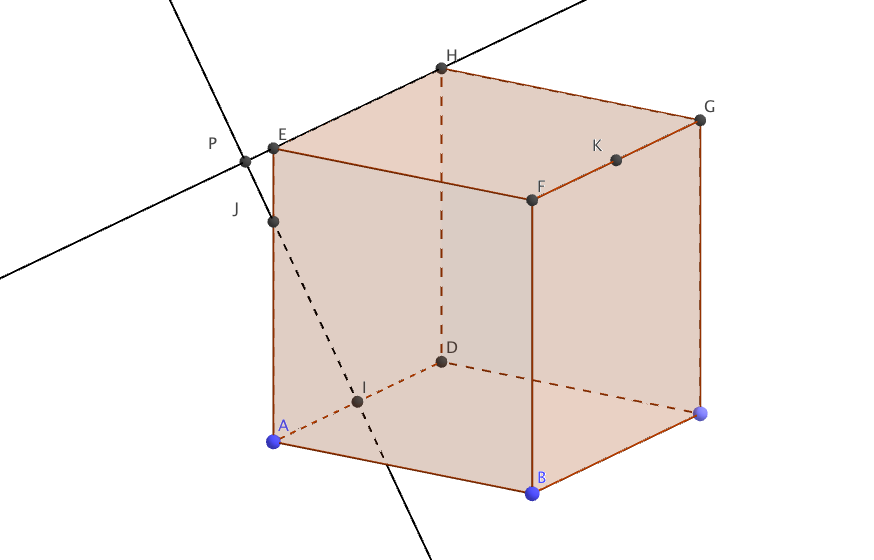 Le point $P$ est l’intersection de la droite $(IJ)$ avec la droite $(EH)$.
Le point $P$ est l’intersection de la droite $(IJ)$ avec la droite $(EH)$.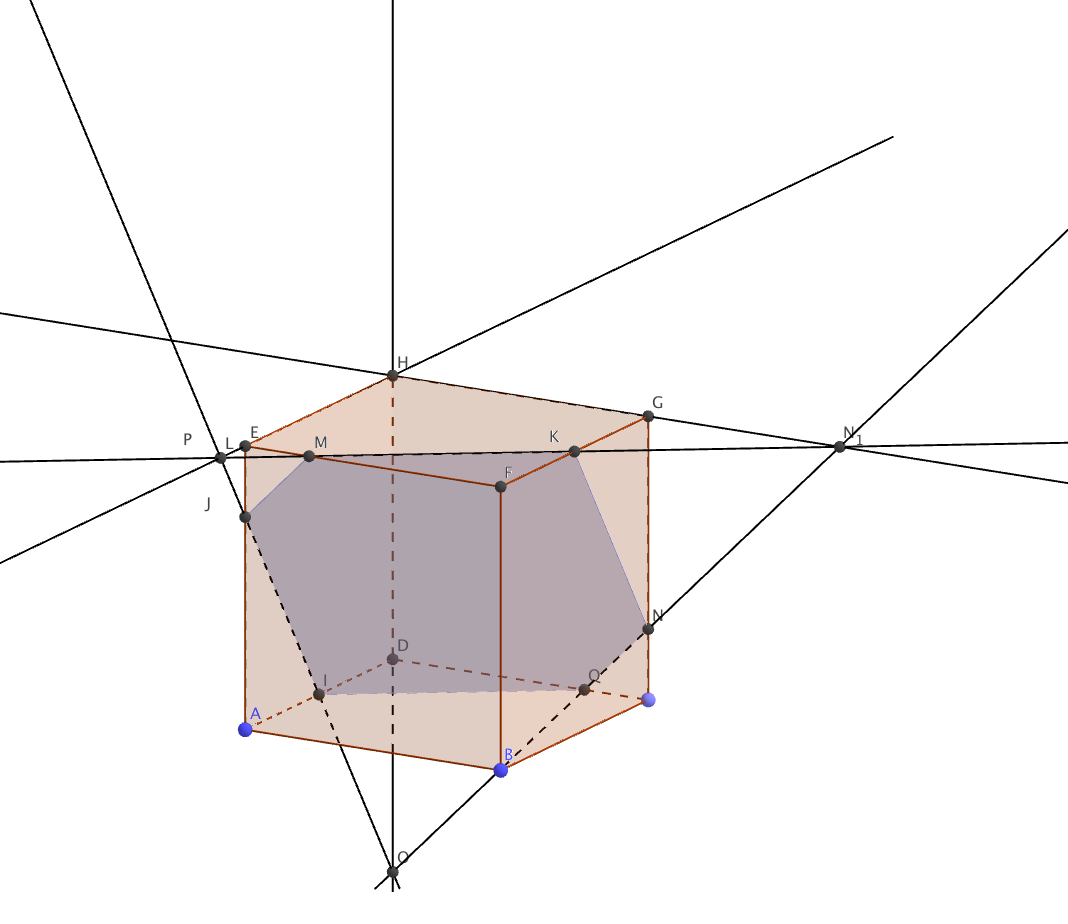
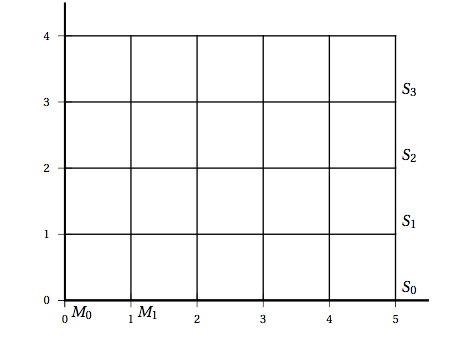
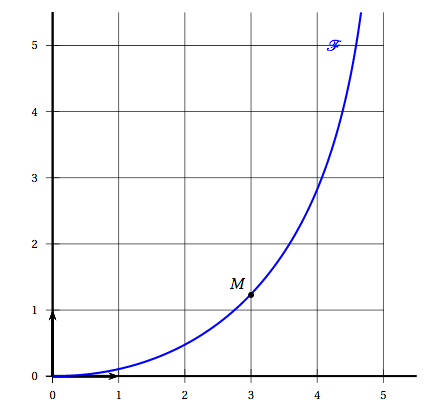
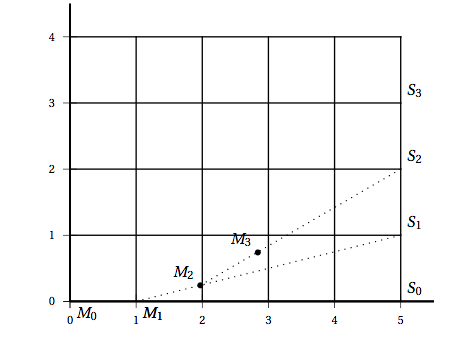
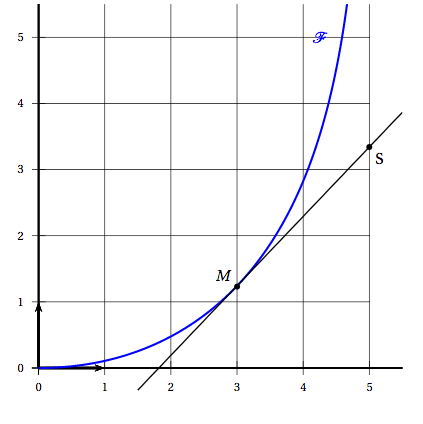 Graphiquement, les coordonnées du point $S$ sont alors $(5;3,3)$.
Graphiquement, les coordonnées du point $S$ sont alors $(5;3,3)$.