Baccalauréat S -- Nouvelle Calédonie 27 novembre 2018
Exercice 1 6 points
Soient $f$ et $g$ les fonctions définies sur $]0~;~+\infty[$ par \[f(x)=\text{e} ^{-x}\quad \text{ et }\quad g(x) = \dfrac{1}{x^2} \text{e} ^{-\frac{1}{x}}.\] On admet que $f$ et $g$ sont dérivables sur $]0~;~+\infty[$. On note $f'$ et $g'$ leurs fonctions dérivées respectives. Les représentations graphiques de $f$ et $g$ dans un repère orthogonal, nommées respectivement $\mathcal{C}_f$ et $\mathcal{C}_g$ sont données ci-dessous: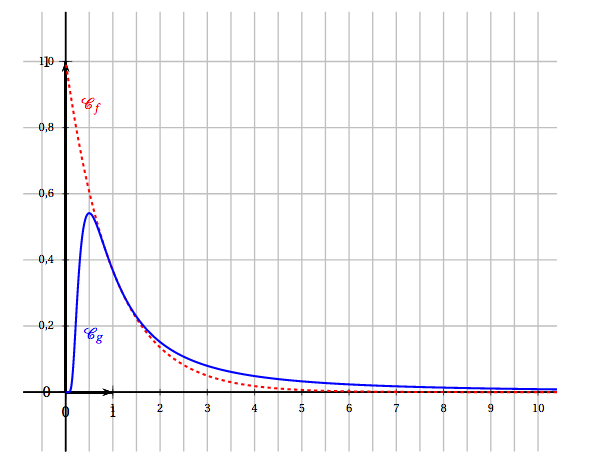
Partie A -- Conjectures graphiques
Dans chacune des questions de cette partie, aucune explication n'est demandée.
- Conjecturer graphiquement une solution de l'équation $f(x)=g(x)$ sur $]0~;~+\infty[$.
- Conjecturer graphiquement une solution de l'équation $g'(x)=0$ sur $]0~;~+\infty[$.
Partie B -- Étude de la fonction $g$
- Calculer la limite de $g(x)$ quand $x$ tend vers $+\infty$.
- On admet que la fonction $g$ est strictement positive sur $]0~;~+\infty[$. Soit $h$ la fonction définie sur $]0~;~+\infty[$ par $h(x)=\ln\left ( g(x) \strut\right )$.
- Démontrer que, pour tout nombre réel $x$ strictement positif, \[h(x)= \dfrac{-1-2x\ln x}{x}.\]
- Calculer la limite de $h(x)$ quand $x$ tend vers 0.
- En déduire la limite de $g(x)$ quand $x$ tend vers 0.
- Démontrer que, pour tout nombre réel $x$ strictement positif, \[g'(x)= \dfrac{\text{e} ^{-\frac{1}{x}}\left (1-2x \strut\right )}{x^4}.\]
- En déduire les variations de la fonction $g$ sur $]0~;~+\infty[$.
Partie C -- Aire des deux domaines compris entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$
- Démontrer que la point A de coordonnées $\left (1~;~\text{e} ^{-1}\strut\right )$ est un point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$.
On admet que ce point est l'unique point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$, et que $\mathcal{C}_f$ est au dessus de $\mathcal{C}_g$ sur l'intervalle $]0~;~1[$ et en dessous sur l'intervalle $]1~;~+\infty[$. - Soient $a$ et $b$ deux réels strictement positifs. Démontrer que \[\displaystyle\int_{a}^{b} \left ( f(x)-g(x)\strut\right ) \text{d} x = \text{e} ^{-a} + \text{e} ^{-\frac{1}{a}} - \text{e} ^{-b} - \text{e} ^{-\frac{1}{b}}.\]
- Démontrer que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =1-2\text{e} ^{-1}.\]
- On admet que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =\displaystyle\lim_{b\to +\infty} \displaystyle\int_{1}^{b} \left ( g(x)-f(x)\strut\right ) \text{d} x .\] Interpréter graphiquement cette égalité.
Correction de l'exercice 1 (6 points)
Soient $f$ et $g$ les fonctions définies sur $]0~;~+\infty[$ par \[f(x)=\text{e} ^{-x}\quad \text{ et }\quad g(x) = \dfrac{1}{x^2} \text{e} ^{-\frac{1}{x}}.\] On admet que $f$ et $g$ sont dérivables sur $]0~;~+\infty[$. On note $f'$ et $g'$ leurs fonctions dérivées respectives. Les représentations graphiques de $f$ et $g$ dans un repère orthogonal, nommées respectivement $\mathcal{C}_f$ et $\mathcal{C}_g$ sont données ci-dessous:
Partie A -- Conjectures graphiques
Dans chacune des questions de cette partie, aucune explication n'est demandée.
- Conjecturer graphiquement une solution de l'équation $f(x)=g(x)$ sur $]0~;~+\infty[$. Graphiquement, une solution de l’équation $f(x)=g(x)$ est $1$.
- Conjecturer graphiquement une solution de l'équation $g'(x)=0$ sur $]0~;~+\infty[$. Graphiquement, une solution de l’équation $g'(x)=0$ est $0,5$ (la dérivée s’annule en l’abscisse d’un sommet).
$\quad$
$\quad$
Partie B -- Étude de la fonction $g$
- Calculer la limite de $g(x)$ quand $x$ tend vers $+\infty$. $\lim\limits_{x\to +\infty} -\dfrac{1}{x}=0$ et $\lim\limits_{X \to 0} \text{e}^X=0$ donc$\lim\limits_{x \to +\infty} \text{e}^{-1/x}=0$.
- On admet que la fonction $g$ est strictement positive sur $]0~;~+\infty[$. Soit $h$ la fonction définie sur $]0~;~+\infty[$ par $h(x)=\ln\left ( g(x) \strut\right )$.
- Démontrer que, pour tout nombre réel $x$ strictement positif, \[h(x)= \dfrac{-1-2x\ln x}{x}.\] Pour tout réel $x$ strictement positif on a :
- Calculer la limite de $h(x)$ quand $x$ tend vers 0. $\lim\limits_{x\to 0^+} x\ln(x)=0$ ( Limite de référence) donc $\lim\limits_{x\to 0^+}-2x\ln(x)-1=-1$.
- En déduire la limite de $g(x)$ quand $x$ tend vers 0. Pour tout réel $x$ strictement positif on a $h(x)=\ln\left(g(x)\right) \iff g(x)=\text{e}^{h(x)}$.
$\begin{align*} h(x)&=\ln\left(g(x)\right) \\
&=\ln\left(\dfrac{1}{x^2}\text{e}^{-1/x}\right) \\
&=\ln\left(\dfrac{1}{x^2}\right)+\ln\left(\text{e}^{-1/x}\right)\\
&=-\ln\left(x^2\right)-\dfrac{1}{x} \\
&=-2\ln(x)-\dfrac{1}{x} \\
&=\dfrac{-2x\ln(x)-1}{x}\end{align*}$
$\quad$
De plus, $\lim\limits_{x\to 0^+} \dfrac{1}{x}=+\infty$.
Donc, par produit de limites, $\lim\limits_{x \to 0^+} h(x)=-\infty$.
$\quad$
Or $\lim\limits_{x \to 0^+} h(x)=-\infty$ et $\lim\limits_{X \to -\infty} =0$.
Donc, par composition de limite on a $\lim\limits_{x \to 0^+} g(x)=0$.
$\quad$ - Démontrer que, pour tout nombre réel $x$ strictement positif, \[g'(x)= \dfrac{\text{e} ^{-\frac{1}{x}}\left (1-2x \strut\right )}{x^4}.\] La fonction $g$ est dérivable sur $]0;+\infty[$ d’après l’énoncé.
- En déduire les variations de la fonction $g$ sur $]0~;~+\infty[$. La fonction exponentielle est strictement positive sur $\mathbb{R}$. De plus, pour tout $x>0$, on a $x^4>0$.
De plus $\lim\limits_{x \to +\infty} \dfrac{1}{x^2}=0$.
Donc, par produit de limites, $\lim\limits_{x \to +\infty} g(x)=0$.
$\quad$
$\begin{align*} g'(x)&=\dfrac{-2}{x^3}\text{e}^{-1/x}+\dfrac{1}{x^2}\times \dfrac{1}{x^2}\text{e}^{-1/x} \\
&=\left(\dfrac{-2}{x^3}+\dfrac{1}{x^4}\right)\text{e}^{-1/x} \\
&=\dfrac{(-2x+1)\text{e}^{-1/x}}{x^4} \end{align*}$
$\quad$
Le signe de $g'(x)$ ne dépend donc que de celui de $1-2x$.
Or $1-2x=0 \iff x=1/2$ et $1-2x>0\iff -2x>-1 \iff x<\dfrac{1}{2}$.
Ainsi $g'(x)<0$ sur l’intervalle $\left]\dfrac{1}{2};+\infty\right[$
$g\left(\dfrac{1}{2}\right)=0$
et $g'(x)>0$ sur l’intervalle $\left]0;\dfrac{1}{2}\right[$.
Par conséquent, la fonction $g$ est croissante sur l’intervalle $\left]0;\dfrac{1}{2}\right[$ et décroissante sur l’intervalle $\left]\dfrac{1}{2};+\infty\right[$.
$\quad$
Partie C -- Aire des deux domaines compris entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$
- Démontrer que la point A de coordonnées $\left (1~;~\text{e} ^{-1}\strut\right )$ est un point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$.
On admet que ce point est l'unique point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$, et que $\mathcal{C}_f$ est au dessus de $\mathcal{C}_g$ sur l'intervalle $]0~;~1[$ et en dessous sur l'intervalle $]1~;~+\infty[$. $f(1)=\text{e}^{-1}$ et $g(1)=\dfrac{1}{1^2}\text{e}^{-1/1}=\text{e}^{-1}$. - Soient $a$ et $b$ deux réels strictement positifs. Démontrer que \[\displaystyle\int_{a}^{b} \left ( f(x)-g(x)\strut\right ) \text{d} x = \text{e} ^{-a} + \text{e} ^{-\frac{1}{a}} - \text{e} ^{-b} - \text{e} ^{-\frac{1}{b}}.\] Pour tout réel $a$ et $b$ strictement positifs on a :
- Démontrer que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =1-2\text{e} ^{-1}.\] $\lim\limits_{a \to 0} \text{e}^{-a}=\text{e}^0=1$
- On admet que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =\displaystyle\lim_{b\to +\infty} \displaystyle\int_{1}^{b} \left ( g(x)-f(x)\strut\right ) \text{d} x .\] Interpréter graphiquement cette égalité. Cette égalité signifie que l’aire du domaine compris entre $\mathscr{C}_f$, $\mathscr{C}_g$ et les droites d’équation $x=0$ et $x=1$ est égale à celle du domaine compris entre $\mathscr{C}_g$ et $\mathscr{C}_f$ pour tous les points dont l’abscisse est supérieure à $1$.
Ainsi le point $A$ de coordonnées $\left(1;\text{e}^{-1}\right)$ est un point d’intersection de $\mathscr{C}_f$ et $\mathscr{C}_g$.
$\quad$
$\begin{align*} \displaystyle \int_a^b \left(f(x)-g(x)\right)\text{d} x &=\int_a^b \left(\text{e}^{-x}-\dfrac{1}{x^2}\text{e}^{-1/x}\right) \text{d} x \\
&=\left[-\text{e}^{-x}-\text{e}^{-1/x}\right]_a^b \\
&=-\text{e}^{-b}-\text{e}^{-1/b}+\text{e}^{-a}+\text{e}^{-1/a} \\
&=\text{e}^{-a}+\text{e}^{-1/a}-\text{e}^{-b}-\text{e}^{-1/b}\end{align*}$
$\quad$
$\lim\limits_{a \to 0^+} -\dfrac{1}{a}=-\infty$ et $\lim\limits_{x \to -\infty} \text{e}^x=0$. Donc $\lim\limits_{a \to 0^+} \text{e}^{-1/a}=0$.
Par conséquent :
$\begin{align*} \displaystyle \lim\limits_{a \to 0^+} \int_a^1 \left(f(x)-g(x)\right)\text{d} x&=1+0-\text{e}^{-1}-\text{e}^{-1} \\
&=1-2\text{e}^{-1}\end{align*}$
$\quad$
$\quad$
Exercice 2 : 3 points
Une épreuve de culture générale consiste en un questionnaire à choix multiple (QCM) de vingt questions. Pour chacune d'entre elles, le sujet propose quatre réponses possibles, dont une seule est correcte. À chaque question, le candidat ou la candidate doit nécessairement choisir une seule réponse. Cette personne gagne un point par réponse correcte et ne perd auxun point si sa réponse est fausse.
On considère trois candidats:
- Anselme répond complètement au hasard à chacune des vingt questions. Autrement dit, pour chacune des questions, la probabilité qu'il réponde correctement est égale à $\dfrac{1}{4}$;
- Barbara est un peu mieux préparée. On considère que pour chacune des vingt questions, la probabilité qu'elle réponde correctement est de $\dfrac{1}{2}$;
- Camille fait encore mieux: pour chacune des questions, la probabilité qu'elle réponde correctement est de $\dfrac{2}{3}$.
- On note $X$, $Y$ et $Z$ les variables aléatoires égales aux notes respectivement obtenues par Anselme, Barbara et Camille.
- Quelle est la loi de probabilité suivie par la variable aléatoire $X$? Justifier.
- À l'aide de la calculatrice, donner l'arrondi au millième de la probabilité $P(X \geqslant 10)$.
- On choisit au hasard la copie d'un de ces trois candidats. On note $A$, $B$, $C$ et $M$ les évènements:
- $A$: « la copie choisie est celle d'Anselme »;
- $B$: « la copie choisie est celle de Barbara »;
- $C$: « la copie choisie est celle de Camille »;
- $M$: « la copie choisie obtient une note supérieure ou égale à 10 ».
On constate, après l'avoir corrigée, que la copie choisie obtient une note supérieure ou égale à 10 sur 20.
Quelle est la probabilité qu'il s'agisse de la copie de Barbara? On donnera l'arrondi au millième de cette probabilité.
Dans la suite, on admettra que $P(Y\geqslant 10) \approx 0,588$ et $P(Z\geqslant 10)\approx 0,962$.
Correction de l'exercice 2 (3 points)
Une épreuve de culture générale consiste en un questionnaire à choix multiple (QCM) de vingt questions. Pour chacune d'entre elles, le sujet propose quatre réponses possibles, dont une seule est correcte. À chaque question, le candidat ou la candidate doit nécessairement choisir une seule réponse. Cette personne gagne un point par réponse correcte et ne perd auxun point si sa réponse est fausse.
On considère trois candidats:
- Anselme répond complètement au hasard à chacune des vingt questions. Autrement dit, pour chacune des questions, la probabilité qu'il réponde correctement est égale à $\dfrac{1}{4}$;
- Barbara est un peu mieux préparée. On considère que pour chacune des vingt questions, la probabilité qu'elle réponde correctement est de $\dfrac{1}{2}$;
- Camille fait encore mieux: pour chacune des questions, la probabilité qu'elle réponde correctement est de $\dfrac{2}{3}$.
- On note $X$, $Y$ et $Z$ les variables aléatoires égales aux notes respectivement obtenues par Anselme, Barbara et Camille.
- Quelle est la loi de probabilité suivie par la variable aléatoire $X$? Justifier. Les vingt questions sont indépendantes. Les “tirages” sont aléatoires, identiques et possèdent deux issues :”Anselme répond correctement” ou non.
- À l'aide de la calculatrice, donner l'arrondi au millième de la probabilité $P(X \geqslant 10)$.
La variable aléatoire $X$ suit donc la loi binomiale de paramètres $n=20$ et $p=0,25$.
$\quad$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$À l’aide de la calculatrice on obtient $P(X\geq 10) =1-P(X\leq 9) \approx 0,014$.
$\quad$ - On choisit au hasard la copie d'un de ces trois candidats. On note $A$, $B$, $C$ et $M$ les évènements:
- $A$: « la copie choisie est celle d'Anselme »;
- $B$: « la copie choisie est celle de Barbara »;
- $C$: « la copie choisie est celle de Camille »;
- $M$: « la copie choisie obtient une note supérieure ou égale à 10 ».
On constate, après l'avoir corrigée, que la copie choisie obtient une note supérieure ou égale à 10 sur 20.
Quelle est la probabilité qu'il s'agisse de la copie de Barbara? On donnera l'arrondi au millième de cette probabilité. D’après la formule des probabilités totales on a :
Dans la suite, on admettra que $P(Y\geqslant 10) \approx 0,588$ et $P(Z\geqslant 10)\approx 0,962$.
$\begin{align*} p(M)&=p(M\cap A)+p(M\cap B)+p(M\cap C) \\
&\approx \dfrac{1}{3}\times 0,014+\dfrac{1}{3}\times 0,588+\dfrac{1}{3}\times 0,962 \\
&\approx 0,521 \end{align*}$
Par conséquent
$\begin{align*} p_M(B)&=\dfrac{p(M\cap B)}{p(M)} \\
&\approx \dfrac{\dfrac{1}{3}\times 0,588}{0,521} \\
&\approx 0,376 \end{align*}$
La probabilité qu’il s’agisse de la copie de Barbara sachant que la note est supérieure ou égale à $10$ est d’environ $0,376$.
$\quad$
Exercice 3 : 6 points
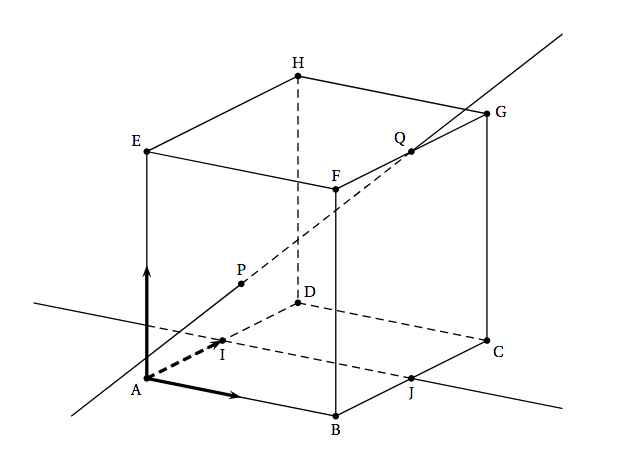
Soit ABCDEFGH le cube représenté ci-dessous.
On considère:
- I et J les milieux respectifs des segments [AD] et [BC];
- P le centre de la face ABFE, c'est-à-dire l'intersection des diagonales (AF) et (BE);
- Q le milieu du segment [FG].
On se place dans le repère orthonormé $\left ( \text{A}~;~\frac{1}{2}\vec{AB}\;,\;\frac{1}{2}\vec{AD}\;,\;\frac{1}{2}\vec{AE}\right )$. Dans tout l'exercice, on pourra utiliser les coordonnées des points de la figure sans les justifier.
On admet qu'une représentation paramétrique de la droite (IJ) est \[\left \lbrace \begin{array}{l !{=} l} x& r\\ y & 1\\ z & 0\\ \end{array} \right . , \quad r\in\mathbb{R}\]
- Vérifier qu'une représentation paramétrique de la droite (PQ) est \[\left \lbrace \begin{array}{l !{=} r} x& 1+t\\ y & t \\ z & 1+t\\ \end{array} \right . ,\quad t\in\mathbb{R}\]
-
- On admet qu'il existe un unique point K appartenant à la droite (IJ) tel que (MK) soit orthogonale à (IJ). Démontrer que les coordonnées de ce point K sont $(1+t~;~1~;~0)$.
- En déduire que $\text{MK} = \sqrt{2+2t^2}$.
-
- Vérifier que $y-z=0$ est une équation cartésienne du plan (HGB).
- On admet qu'il existe un unique point L appartenant au plan (HGB) tel que (ML) soit orthogonale à (HGB).
Vérifier que les coordonnées de ce point L sont $\left (1+t~;~\dfrac{1}{2}+t~;~\dfrac{1}{2}+t\right )$. - En déduire que la distance ML est indépendante de $t$.
- Existe-t-il une valeur de $t$ pour laquelle la distance MK est égale à la distance ML?
Soient $t$ un nombre réel et M $(1+t~;~t~;~1+t)$ le point de la droite (PQ) de paramètre $t$.
Correction de l'exercice 3 (6 points)
Soit ABCDEFGH le cube représenté ci-dessous.
On considère:
- I et J les milieux respectifs des segments [AD] et [BC];
- P le centre de la face ABFE, c'est-à-dire l'intersection des diagonales (AF) et (BE);
- Q le milieu du segment [FG].

On se place dans le repère orthonormé $\left ( \text{A}~;~\frac{1}{2}\vec{AB}\;,\;\frac{1}{2}\vec{AD}\;,\;\frac{1}{2}\vec{AE}\right )$. Dans tout l'exercice, on pourra utiliser les coordonnées des points de la figure sans les justifier.
On admet qu'une représentation paramétrique de la droite (IJ) est \[\left \lbrace \begin{array}{l !{=} l} x& r\\ y & 1\\ z & 0\\ \end{array} \right . , \quad r\in\mathbb{R}\]
- Vérifier qu'une représentation paramétrique de la droite (PQ) est \[\left \lbrace \begin{array}{l !{=} r} x& 1+t\\ y & t \\ z & 1+t\\ \end{array} \right . ,\quad t\in\mathbb{R}\] Le point $P$ a pour coordonnées $(1;0;1)$.
-
- On admet qu'il existe un unique point K appartenant à la droite (IJ) tel que (MK) soit orthogonale à (IJ). Démontrer que les coordonnées de ce point K sont $(1+t~;~1~;~0)$. Les coordonnées du point $I$ sont $(0;1;0)$ et celles du point $J$ sont $(2;1;0)$.
- En déduire que $\text{MK} = \sqrt{2+2t^2}$.
Ainsi les coordonnées du vecteur $\vec{IJ}$ sont $(2;0;0)$.
On considère le point $K’$ de coordonnées $(1+t;1;0)$.
Alors les coordonnées du vecteur $\vec{MK’}$ sont $(0;1-t;-1-t)$.
$\vec{IJ}.\vec{MK’}=0+0+0=0$.
Les vecteurs $\vec{IJ}$ et $\vec{MK’}$ sont orthogonaux.
$\quad$
Une représentation paramétrique de la droite $(IJ)$ est $\begin{cases} x=r\\y=1\\z=0\end{cases}, \quad r\in \mathbb{R}$.
En prenant $r=1+t$ on obtient le fait que $K’$ appartient à la droite $(IJ)$.
$\quad$
Le point $K’$ appartient à la droite $(IJ)$ et est tel que $(MK’)$ soit orthogonal à $(IJ)$. Un tel point est unique d’après l’énoncé.
Par conséquent les coordonnées du point $K$ sont bien $(1+t;1;0)$.
$\quad$
$\begin{align*} MK&=\left\| \vec{MK}\right\| \\
&=\sqrt{0^2+(1-t)^2+(-1-t)^2} \\
&=\sqrt{1-2t+t^2+1+2t+t^2}\\
&=\sqrt{2+2t^2}\end{align*}$
$\quad$ -
- Vérifier que $y-z=0$ est une équation cartésienne du plan (HGB). Le point $H$ a pour coordonnées $(0;2;2)$ et $y_H-z_H=2-2=0$. Donc $H$ appartient au plan d’équation $y-z=0$.
- On admet qu'il existe un unique point L appartenant au plan (HGB) tel que (ML) soit orthogonale à (HGB).
Vérifier que les coordonnées de ce point L sont $\left (1+t~;~\dfrac{1}{2}+t~;~\dfrac{1}{2}+t\right )$. On note $L’$ le point de coordonnées $\left(1+t;\dfrac{1}{2}+t;\dfrac{1}{2}+t\right)$. - En déduire que la distance ML est indépendante de $t$.
Le point $G$ a pour coordonnées $(2;2;2)$ et $y_G-z_G=2-2=0$. Donc $G$ appartient au plan d’équation $y-z=0$.
Le point $B$ a pour coordonnées $(2;0;0)$ et $y_B-z_B=0-0=0$. Donc $B$ appartient au plan d’équation $y-z=0$.
Ainsi, une équation cartésienne du plan $(HGB)$ est $y-z=0$.
$\quad$
$y_L-z_L=\dfrac{1}{2}+t-\dfrac{1}{2}-t=0$ donc $L’$ appartient au plan $(HGB)$.
$\quad$
Les coordonnées du vecteur $\vec{ML’}$ sont $\left(0;\dfrac{1}{2}+t-t;\dfrac{1}{2}+t-1-t\right)$ soit $\left(0;\dfrac{1}{2};-\dfrac{1}{2}\right)$.
Un vecteur normal au plan $(HGB)$ est $\vec{n}(0;1;-1)$.
Par conséquent $\vec{ML’}=\dfrac{1}{2}\vec{n}$.
Le vecteur $\vec{ML’}$ est bien orthogonal au plan $(HGB)$.
$\quad$
Le point $L’$ appartient au plan $(HGB)$ et est tel que $(ML’)$ soit orthogonal à $(HGB)$. Un tel point est unique.
Les coordonnées du point $L$ sont donc $\left(0;\dfrac{1}{2}+t-t;\dfrac{1}{2}+t-1-t\right)$.
$\quad$
$\begin{align*} ML&=\left\| \vec{ML}\right\| \\
&=\sqrt{0^2+\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2} \\
&=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}\\
&=\sqrt{\dfrac{1}{2}}\\
&=\dfrac{\sqrt{2}}{2}\end{align*}$
$\quad$ - Existe-t-il une valeur de $t$ pour laquelle la distance MK est égale à la distance ML? On veut résoudre l’équation :
Le point $F$ a pour coordonnées $(2;0;2)$ et le point $G$ a pour coordonnées $(2;2;2)$.
Ainsi le point $Q$ a pour coordonnées $\left(\dfrac{2+2}{2};\dfrac{0+2}{2};\dfrac{2+2}{2}\right)$ soit $(2;1;2)$.
Dans la représentation paramétrique proposée :
$\bullet$ Si $t=0$ alors $\begin{cases} x=1\\y=0\\z=1\end{cases}$ et on obtient les coordonnées du point $P$.
$\bullet$ Si $t=1$ alors $\begin{cases} x=2\\y=1\\z=2\end{cases}$ et on obtient les coordonnées du point $Q$.
Une représentation paramétrique de la droite $(PQ)$ est donc bien $\begin{cases} x=1+t\\y=t\\z=1+t\end{cases}, \quad t\in \R$.
$\quad$
Soient $t$ un nombre réel et M $(1+t~;~t~;~1+t)$ le point de la droite (PQ) de paramètre $t$.
$ ML=MK \iff \sqrt{\dfrac{1}{2}}=\sqrt{2+2t^2}$
Or, pour tout réel $t$ on a $2+2t^2\geq 2>\dfrac{1}{2}$.
Il n’existe donc pas de valeur de $t$ pour laquelle la distance $MK$ est égale à la distance $ML$.
$\quad$
Exercice 4 5 points
On définit la suite de nombres complexes $(z_n)$ de la manière suivante: $z_0=1$ et, pour tout entier naturel $n$, \[z_{n+1} = \dfrac{1}{3} z_{n} + \dfrac{2}{3}\text{i}.\] On se place dans un plan muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour tout entier naturel $n$, on note A$_{n}$ le point du plan d'affixe $z_n$. Pour tout entier naturel $n$, on pose $u_n=z_n-\text{i}$ et on note B$_n$ le point d'affixe $u_n$. On note C le point d'affixe $\text{i}$.
- Exprimer $u_{n+1}$ en fonction de $u_n$, pour tout entier naturel $n$.
- Démontrer que, pour tout entier naturel $n$, \[u_n=\left (\dfrac{1}{3}\right )^{n} \left (1-\text{i}\right ).\]
-
- Pour tout entier naturel $n$, calculer, en fonction de $n$, le module de $u_n$.
- Démontrer que \[\lim_{n\to +\infty} \left |z_n-\text{i} \right |=0.\]
- Quelle interprétation géométrique peut-on donner de ce résultat?
-
- Soit $n$ un entier naturel. déterminer un argument de $u_n$.
- Démontrer que, lorsque $n$ décrit l'ensemble des entiers naturels, les points B$_n$ sont alignés.
- Démontrer que, pour tout entier naturel $n$, le point A$_n$ appartient à la droite d'équation réduite: \[y=-x+1.\]
Correction de l'exercice 4 5 points
On définit la suite de nombres complexes $(z_n)$ de la manière suivante: $z_0=1$ et, pour tout entier naturel $n$, \[z_{n+1} = \dfrac{1}{3} z_{n} + \dfrac{2}{3}\text{i}.\] On se place dans un plan muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour tout entier naturel $n$, on note A$_{n}$ le point du plan d'affixe $z_n$. Pour tout entier naturel $n$, on pose $u_n=z_n-\text{i}$ et on note B$_n$ le point d'affixe $u_n$. On note C le point d'affixe $\text{i}$.
- Exprimer $u_{n+1}$ en fonction de $u_n$, pour tout entier naturel $n$. Pour tout entier naturel $n$ on a :
- Démontrer que, pour tout entier naturel $n$, \[u_n=\left (\dfrac{1}{3}\right )^{n} \left (1-\text{i}\right ).\] Démontrons, par récurrence sur $n$, que, pour tout entier naturel $n$ on a $u_n=\left(\dfrac{1}{3}\right)^n(1-\text{i})$.
-
- Pour tout entier naturel $n$, calculer, en fonction de $n$, le module de $u_n$. Pour tout entier naturel $n$ on a :
- Démontrer que \[\lim_{n\to +\infty} \left |z_n-\text{i} \right |=0.\] $-1 < \dfrac{1}{3} <1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{1}{3}\right)^n=0$.
- Quelle interprétation géométrique peut-on donner de ce résultat? Géométriquement, cela signifie que, pour de grandes valeur de $n$, le point $A_n$ est très proche du point $C$.
$\begin{align*}\left|u_n\right|&=\left|\left(\dfrac{1}{3}\right)^n(1-\text{i})\right| \\
&=\left(\dfrac{1}{3}\right)^n\left|1-\text{i}\right| \\
&=\left(\dfrac{1}{3}\right)^n\times \sqrt{1^2+(-1)^2} \\
&=\sqrt{2}\times \left(\dfrac{1}{3}\right)^n\end{align*}$
$\quad$
Par conséquent $\lim\limits_{n \to +\infty} \left|u_n\right|=0$
C’est-à-dire $\lim\limits_{n \to +\infty} \left|z_n-\text{i}\right|=0$.
$\quad$
$\quad$ O -
- Soit $n$ un entier naturel. déterminer un argument de $u_n$. n a $|1-\text{i}|=\sqrt{2}$ donc $1-\text{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\text{i}\right)=\sqrt{2}\text{e}^{-\text{i}\pi/4}$.
- Démontrer que, lorsque $n$ décrit l'ensemble des entiers naturels, les points B$_n$ sont alignés. On considère deux entiers naturels non nuls $n$ et $m$.
- Démontrer que, pour tout entier naturel $n$, le point A$_n$ appartient à la droite d'équation réduite: \[y=-x+1.\] On a $u_0=1-\text{i}$. Une équation de la droite $\left(OB_0\right)$ est donc $y=-x$.
Par conséquent $u_n=\left(\dfrac{1}{3}\right)^n\times \sqrt{2}\text{e}^{-\text{i}\pi/4}$.
Un argument de $u_n$ est donc $-\dfrac{\pi}{4}$.
$\quad$
L’affixe du vecteur $\vec{B_0B_n}$ est
$\begin{align*} c_n&=u_n-u_0\\
&=\left(\dfrac{1}{3}\right)^n(1-\text{i})-(1-\text{i}) \\
&=(1-\text{i})\times \left(\left(\dfrac{1}{3}\right)^n-1\right) \end{align*}$
L’affixe du vecteur $\vec{B_0B_m}$ est
$\begin{align*} d_n&=u_m-u_0\\
&=\left(\dfrac{1}{3}\right)^m(1-\text{i})-(1-\text{i}) \\
&=(1-\text{i})\times \left(\left(\dfrac{1}{3}\right)^m-1\right) \end{align*}$
Par conséquent $d_n=\dfrac{\left(\dfrac{1}{3}\right)^m-1}{\left(\dfrac{1}{3}\right)^n-1}c_n$.
Les vecteurs $\vec{B_0B_n}$ et $\vec{B_0B_m}$ sont colinéaires.
Les points $B_0$, $B_n$ et $B_m$ sont donc alignés.
$\quad$
Autre méthode :
On considère deux entiers naturels $n$ et $m$.
$\begin{align*} \left(\vec{OB_n},\vec{OB_m}\right)&=\left(\vec{u},\vec{OB_m}\right)-\left(\vec{OB_n},\vec{u}\right) \\
&=-\dfrac{\pi}{4}-\left(-\dfrac{\pi}{4}\right) ~~[2\pi] \\
&=0~~[2\pi]\end{align*}$
Les points $O$, $B_n$ et $B_M$ sont donc alignés.
Cela signifie donc que tous les points $B_n$ appartiennent à la droite $\left(OB_0\right)$.
$\quad$
Pour tout entier naturel $n$, il existe donc un réel $x_n$ tel que m’affixe du point $B_n$ soit $u_n=x_n(1-\text{i})$.
Or l’affixe du point $B_n$ est $u_n=z_n-\text{i}$.
Par conséquent, en notant $a_n+\text{i} b_n$ la forme algébrique de $z_n$ on a :
$\begin{align*} x_n(1-\text{i})=a_n+\text{i} b_n-\text{i} &\iff \begin{cases} a_n=x_n \\-x_n=b_n-1\end{cases} \\
&\iff \begin{cases} a_n=x_n \\b_n=-a_n+1\end{cases} \end{align*}$
Le point $A_n$ appartient donc à la droite d’équation $y=-x+1$.
$\quad$
$\begin{align*} u_{n+1}&=z_{n+1}-\text{i} \\
&=\dfrac{1}{3}z_n+\dfrac{2}{3}\text{i}-\text{i} \\
&=\dfrac{1}{3}z_n-\dfrac{1}{3}\text{i} \\
&=\dfrac{1}{3}\left(z_n-\text{i}\right)\\
&=\dfrac{1}{3}u_n\end{align*}$
$\quad$
Initialisation :
Si $n=0$ alors $\left(\dfrac{1}{3}\right)^n(1-\text{i})=1-\text{i}=z_0-\text{i}=u_0$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons que la propriété soit vraie au rang $n$, c’est-à-dire que $u_n=\left(\dfrac{1}{3}\right)^n(1-\text{i})$.
Montrons qu’elle est encore vraie au rang $n+1$ c’est-à-dire que $u_{n+1}=\left(\dfrac{1}{3}\right)^{n+1}(1-\text{i})$
$\begin{align*} u_{n+1}&=\dfrac{1}{3}u_n \\
&=\dfrac{1}{3}\times \left(\dfrac{1}{3}\right)^n(1-\text{i})\\
&=\left(\dfrac{1}{3}\right)^{n+1}(1-\text{i}) \end{align*}$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $u_n=\left(\dfrac{1}{3}\right)^n(1-\text{i})$.
$\quad$
Spécialité 5 points
On appelle suite de Fibonacci la suite $(u_n)$ définie par $u_0=0$, $u_1=1$ et, pour tout entier naturel $n$, \[u_{n+2} = u_{n+1} + u_{n}.\] On admet que, pour tout entier naturel $n$, $u_n$ est un entier naturel.
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
-
- Calculer les termes de la suite de Fibonacci jusqu'à $u_{10}$.
- Que peut-on conjecturer sur le PGCD de $u_{n}$ et $u_{n+1}$ pour tout entier naturel $n$?
- On définit la suite $(v_n)$ par $v_n=u_n^2 - u_{n+1}\times u_{n-1}$ pour tout entier naturel $n$ non nul.
- Démontrer que, pour tout entier naturel $n$ non nul, $v_{n+1} = -v_n$.
- En déduire que, pour tout entier naturel $n$ non nul, \[u_n^2 - u_{n+1}\times u_{n-1} = \left (-1\right )^{n-1}.\]
- Démontrer alors la conjecture émise à la question 1. b.
Partie B
On considère la matrice $F=\begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}$.
- Calculer $F^2$ et $F^3$. On pourra utiliser la calculatrice.
- Démontrer par récurrence que, pour tout entier naturel $n$ non nul, \[F^n = \begin{pmatrix} u_{n+1} & u_n \\ u_n & u_{n-1} \end{pmatrix}\]
-
- Soit $n$ un entier naturel non nul. En remarquant que $F^{2n+2} = F^{n+2}\times F^{n}$, démontrer que \[u_{2n+2} =u_{n+2}\times u_{n+1}+ u_{n+1}\times u_n.\]
- En déduire que, pour tout entier naturel $n$ non nul, \[u_{2n+2} = u_{n+2}^2 - u_n^2.\]
- On donne $u_{12}=144$. Démontrer en utilisant la question 3. qu'il existe un triangle rectangle dont les longueurs des côtés sont toutes des nombres entiers, l'une étant égale à 12. Donner la longueur des deux autres côtés.
Correction de l'exercice de Spécialité 5 points
On appelle suite de Fibonacci la suite $(u_n)$ définie par $u_0=0$, $u_1=1$ et, pour tout entier naturel $n$, \[u_{n+2} = u_{n+1} + u_{n}.\] On admet que, pour tout entier naturel $n$, $u_n$ est un entier naturel.
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
-
- Calculer les termes de la suite de Fibonacci jusqu'à $u_{10}$. On a :
- Que peut-on conjecturer sur le PGCD de $u_{n}$ et $u_{n+1}$ pour tout entier naturel $n$? Il semblerait que pour tout entier naturel $n$ le PGCD de $u_n$ et de $u_{n+1}$ soit égal à $1$.
$u_0=0$, $u_1=1$, $u_2=1$, $u_3=2$, $u_4=3$, $u_5=5$, $u_6=8$, $u_7=13$, $u_8=21$, $u_9=34$ et $u_{10}=55$
$\quad$
$\quad$ - On définit la suite $(v_n)$ par $v_n=u_n^2 - u_{n+1}\times u_{n-1}$ pour tout entier naturel $n$ non nul.
- Démontrer que, pour tout entier naturel $n$ non nul, $v_{n+1} = -v_n$. Soit $n$ un entier naturel non nul.
- En déduire que, pour tout entier naturel $n$ non nul, \[u_n^2 - u_{n+1}\times u_{n-1} = \left (-1\right )^{n-1}.\] La suite $\left(v_n\right)$ est donc géométrique de raison $-1$ et de premier terme $v_1={u_1}^2-u_2\times u_0=1$.
- Démontrer alors la conjecture émise à la question 1. b. Soit $n$ un entier naturel $n$ non nul.
$\begin{align*} v_{n+1}&={u_{n+1}}^2-u_{n+2}\times u_n \\
&={u_{n+1}}^2-\left(u_{n+1}+u_n\right)\times u_n \\
&={u_{n+1}}^2-u_{n+1}\times u_n-{u_n}^2 \\
&=-{u_n}^2+u_{n+1}\left(u_{n+1}-u_n\right)\end{align*}$
Or, $u_{n+1}=u_n+u_{n-1} \iff u_{n-1}=u_{n+1}-u_n$.
Par conséquent $v_{n+1}=-{u_n}^2+u_{n+1}\times u_{n-1}=-v_n$.
$\quad$
Ainsi, pour tout entier naturel $n$ non nul on a $v_n=(-1)^{n-1}$.
Par conséquent ${u_n}^2-u_{n+1}\times u_{n-1}=(-1)^{n-1}$.
$\quad$
Si $n$ est impair alors $n-1$ est pair et
${u_n}^2-u_{n+1}\times u_{n-1}=1$
$\iff u_n\times u_n-u_{n+1}\times u_{n-1}=1$
D’après le théorème de Bezout les nombres $u_n$ et $u_{n+1}$ sont premiers entre eux.
$\quad$
Si $n$ est pair alors $n-1$ est impair et
${u_n}^2-u_{n+1}\times u_{n-1}=-1$
$\iff -{u_n}^2+u_{n+1}\times u_{n-1}=1$
$\iff -u_n\times u_n++u_{n+1}\times u_{n-1}=1$
D’après le théorème de Bezout les nombres $u_n$ et $u_{n+1}$ sont premiers entre eux.
La conjecture de la question est donc vraie pour tout entier naturel $n$ non nul.
De plus le PGCD de $0$ et $1$ est $1$. La conjecture est également vraie pour $n=0$.
La conjecture de la question est donc vraie pour tout entier naturel $n$.
$\quad$
Partie B
On considère la matrice $F=\begin{pmatrix} 1 & 1 \\ 1 & 0\end{pmatrix}$.
- Calculer $F^2$ et $F^3$. On pourra utiliser la calculatrice. On a $F^2=\begin{pmatrix}2&1\\1&1\end{pmatrix}$ et $F^3=\begin{pmatrix}3&2\\2&1\end{pmatrix}$.
- Démontrer par récurrence que, pour tout entier naturel $n$ non nul, \[F^n = \begin{pmatrix} u_{n+1} & u_n \\ u_n & u_{n-1} \end{pmatrix}\] Montrons cette propriété par récurrence.
-
- Soit $n$ un entier naturel non nul. En remarquant que $F^{2n+2} = F^{n+2}\times F^{n}$, démontrer que \[u_{2n+2} =u_{n+2}\times u_{n+1}+ u_{n+1}\times u_n.\] Pour tout entier naturel $n$ on a $u_{n+2}=u_{n+1}+u_n$ soit $u_{n+1}=u_{n+2}-u_n$
- En déduire que, pour tout entier naturel $n$ non nul, \[u_{2n+2} = u_{n+2}^2 - u_n^2.\] Soit $n$ un entier naturel non nul.
Ainsi, pour tout entier naturel $n$ non nul, on a :
$\begin{align*} u_{2n+2}&=u_{n+2}\times u_{n+1}+u_{n+1}\times u_n \\
&=u_{n+1}\left(u_{n+2}+u_n\right) \\
&=\left(u_{n+2}-u_n\right)\left(u_{n+2}+u_n\right) \\
&={u_{n+2}}^2-{u_n}^2\end{align*}$
$\quad$
$F^{2n+2}=F^{n+2+n}=F^{n+2}\times F_n$.
Par conséquent :
$\begin{pmatrix} u_{2n+3}&u_{2n+2}\\u_{2n+2}&u_{2n+1}\end{pmatrix}=\begin{pmatrix} u_{n+3}&u_{n+2}\\u_{n+2}&u_{n+1}\end{pmatrix}\times \begin{pmatrix} u_{n+1}&u_n\\u_n&u_{n-1}\end{pmatrix}$
En identifiant les coefficients de la $2$ieme ligne, $1^{\text{ère}}$ colonne on obtient $u_{2n+2}=u_{n+2}\times u_{n+1}+u_{n+1}\times u_n$.
$\quad$ - On donne $u_{12}=144$. Démontrer en utilisant la question 3. qu'il existe un triangle rectangle dont les longueurs des côtés sont toutes des nombres entiers, l'une étant égale à 12. Donner la longueur des deux autres côtés. D’après la question précédente on a, pour tout entier naturel $n$ non nul, ${u_{n+2}}^2=u_{2n+2}+{u_n}^2$
$\quad$
Initialisation : Si $n=1$ alors $F^1=\begin{pmatrix}1&1\\1&0\end{pmatrix}=\begin{pmatrix}u_2&u_1\\u_1&u_0\end{pmatrix}$.
La propriété est vraie au rang $1$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$, c’est à dire $F^n=\begin{pmatrix}u_{n+1}&u_n\\u_n&u_{n-1}\end{pmatrix}$.
Montrons que la propriété est encore vraie au rang $n+1$, soit $F^{n+1}=\begin{pmatrix}u_{n+2}&u_{n+1}\\u_{n+1}&u_{n}\end{pmatrix}$.
$\begin{align*} F^{n+1}&=F\times F_n \\
&=\begin{pmatrix}1&1\\1&0\end{pmatrix}\times \begin{pmatrix}u_{n+1}&u_n\\u_n&u_{n-1}\end{pmatrix} \\
&=\begin{pmatrix} u_{n+1}+u_n&u_n+u_{n-1}\\u_{n+1}&u_n\end{pmatrix} \\
&=\begin{pmatrix} u_{n+2}&u_{n+1}\\u_{n+1}&u_n\end{pmatrix}\end{align*}$
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul, on a $F_n=\begin{pmatrix} u_{n+1}&u_n\\u_n&u_{n-1}\end{pmatrix}$.
$\quad$
La solution de l’équation $2n+2=12$ est $n=5$.
Par conséquent :
${u_7}^2=u_{12}+{u_5}^2$
$\iff 13^2=144+5^2$
$\iff 13^2=12^2+5^2$
D’après la réciproque du théorème de Pythagore, un triangle dont les côtés mesurent $5$, $12$ et $13$ unités est rectangle.
$\quad$
- Vues: 29789
