Baccalauréat S -- Nouvelle Calédonie 27 novembre 2018 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (6 points)

Commun à tous les candidats

Soient $f$ et $g$ les fonctions définies sur $]0~;~+\infty[$ par \[f(x)=\text{e} ^{-x}\quad \text{ et }\quad g(x) = \dfrac{1}{x^2} \text{e} ^{-\frac{1}{x}}.\] On admet que $f$ et $g$ sont dérivables sur $]0~;~+\infty[$. On note $f'$ et $g'$ leurs fonctions dérivées respectives. Les représentations graphiques de $f$ et $g$ dans un repère orthogonal, nommées respectivement $\mathcal{C}_f$ et $\mathcal{C}_g$ sont données ci-dessous: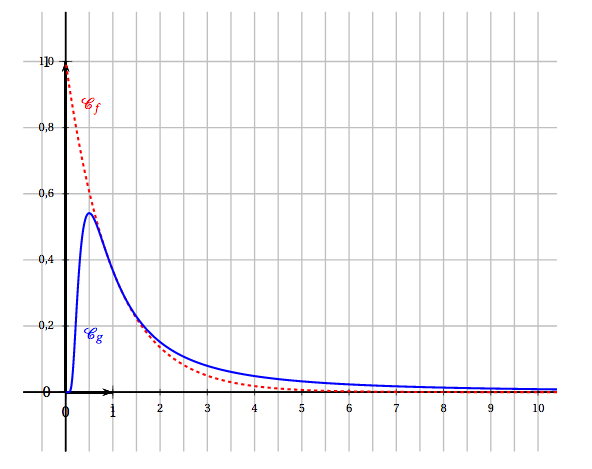

Partie A -- Conjectures graphiques

Dans chacune des questions de cette partie, aucune explication n'est demandée.

1. Conjecturer graphiquement une solution de l'équation $f(x)=g(x)$ sur $]0~;~+\infty[$.
Graphiquement, une solution de l’équation $f(x)=g(x)$ est $1$.
$\quad$
2. Conjecturer graphiquement une solution de l'équation $g'(x)=0$ sur $]0~;~+\infty[$.
Graphiquement, une solution de l’équation $g'(x)=0$ est $0,5$ (la dérivée s’annule en l’abscisse d’un sommet).
$\quad$

 

Partie B -- Étude de la fonction $g$

 

1. Calculer la limite de $g(x)$ quand $x$ tend vers $+\infty$.
$\lim\limits_{x\to +\infty} -\dfrac{1}{x}=0$ et $\lim\limits_{X \to 0} \text{e}^X=0$ donc$\lim\limits_{x \to +\infty} \text{e}^{-1/x}=0$.
De plus $\lim\limits_{x \to +\infty} \dfrac{1}{x^2}=0$.
Donc, par produit de limites, $\lim\limits_{x \to +\infty} g(x)=0$.
$\quad$
2. On admet que la fonction $g$ est strictement positive sur $]0~;~+\infty[$. Soit $h$ la fonction définie sur $]0~;~+\infty[$ par $h(x)=\ln\left ( g(x) \strut\right )$.
   1. Démontrer que, pour tout nombre réel $x$ strictement positif, \[h(x)= \dfrac{-1-2x\ln x}{x}.\]
   Pour tout réel $x$ strictement positif on a :
   $\begin{align*} h(x)&=\ln\left(g(x)\right) \\
   &=\ln\left(\dfrac{1}{x^2}\text{e}^{-1/x}\right) \\
   &=\ln\left(\dfrac{1}{x^2}\right)+\ln\left(\text{e}^{-1/x}\right)\\
   &=-\ln\left(x^2\right)-\dfrac{1}{x} \\
   &=-2\ln(x)-\dfrac{1}{x} \\
   &=\dfrac{-2x\ln(x)-1}{x}\end{align*}$
   $\quad$
   
   2. Calculer la limite de $h(x)$ quand $x$ tend vers 0.
   $\lim\limits_{x\to 0^+} x\ln(x)=0$ ( Limite de référence) donc $\lim\limits_{x\to 0^+}-2x\ln(x)-1=-1$.
   De plus, $\lim\limits_{x\to 0^+} \dfrac{1}{x}=+\infty$.
   Donc, par produit de limites, $\lim\limits_{x \to 0^+} h(x)=-\infty$.
   $\quad$
   
   3. En déduire la limite de $g(x)$ quand $x$ tend vers 0.
   Pour tout réel $x$ strictement positif on a $h(x)=\ln\left(g(x)\right) \iff g(x)=\text{e}^{h(x)}$.
   Or $\lim\limits_{x \to 0^+} h(x)=-\infty$ et $\lim\limits_{X \to -\infty} =0$.
   Donc, par composition de limite on a $\lim\limits_{x \to 0^+} g(x)=0$.
   $\quad$
3. Démontrer que, pour tout nombre réel $x$ strictement positif, \[g'(x)= \dfrac{\text{e} ^{-\frac{1}{x}}\left (1-2x \strut\right )}{x^4}.\]
La fonction $g$ est dérivable sur $]0;+\infty[$ d’après l’énoncé.
$\begin{align*} g'(x)&=\dfrac{-2}{x^3}\text{e}^{-1/x}+\dfrac{1}{x^2}\times \dfrac{1}{x^2}\text{e}^{-1/x} \\
&=\left(\dfrac{-2}{x^3}+\dfrac{1}{x^4}\right)\text{e}^{-1/x} \\
&=\dfrac{(-2x+1)\text{e}^{-1/x}}{x^4} \end{align*}$
$\quad$
4. En déduire les variations de la fonction $g$ sur $]0~;~+\infty[$.
La fonction exponentielle est strictement positive sur $\mathbb{R}$. De plus, pour tout $x>0$, on a $x^4>0$.
Le signe de $g'(x)$ ne dépend donc que de celui de $1-2x$.
Or $1-2x=0 \iff x=1/2$ et $1-2x>0\iff -2x>-1 \iff x<\dfrac{1}{2}$.
Ainsi $g'(x)<0$ sur l’intervalle $\left]\dfrac{1}{2};+\infty\right[$
$g\left(\dfrac{1}{2}\right)=0$
et $g'(x)>0$ sur l’intervalle $\left]0;\dfrac{1}{2}\right[$.
Par conséquent, la fonction $g$ est croissante sur l’intervalle $\left]0;\dfrac{1}{2}\right[$ et décroissante sur l’intervalle $\left]\dfrac{1}{2};+\infty\right[$.
$\quad$

 

Partie C -- Aire des deux domaines compris entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$

 

1. Démontrer que la point A de coordonnées $\left (1~;~\text{e} ^{-1}\strut\right )$ est un point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$.
   On admet que ce point est l'unique point d'intersection de $\mathcal{C}_f$ et $\mathcal{C}_g$, et que $\mathcal{C}_f$ est au dessus de $\mathcal{C}_g$ sur l'intervalle $]0~;~1[$ et en dessous sur l'intervalle $]1~;~+\infty[$.
$f(1)=\text{e}^{-1}$ et $g(1)=\dfrac{1}{1^2}\text{e}^{-1/1}=\text{e}^{-1}$.
Ainsi le point $A$ de coordonnées $\left(1;\text{e}^{-1}\right)$ est un point d’intersection de $\mathscr{C}_f$ et $\mathscr{C}_g$.
$\quad$
2. Soient $a$ et $b$ deux réels strictement positifs. Démontrer que \[\displaystyle\int_{a}^{b} \left ( f(x)-g(x)\strut\right ) \text{d} x = \text{e} ^{-a} + \text{e} ^{-\frac{1}{a}} - \text{e} ^{-b} - \text{e} ^{-\frac{1}{b}}.\]
Pour tout réel $a$ et $b$ strictement positifs on a :
$\begin{align*} \displaystyle \int_a^b \left(f(x)-g(x)\right)\text{d} x &=\int_a^b \left(\text{e}^{-x}-\dfrac{1}{x^2}\text{e}^{-1/x}\right) \text{d} x \\
&=\left[-\text{e}^{-x}-\text{e}^{-1/x}\right]_a^b \\
&=-\text{e}^{-b}-\text{e}^{-1/b}+\text{e}^{-a}+\text{e}^{-1/a} \\
&=\text{e}^{-a}+\text{e}^{-1/a}-\text{e}^{-b}-\text{e}^{-1/b}\end{align*}$
$\quad$
3. Démontrer que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =1-2\text{e} ^{-1}.\]
$\lim\limits_{a \to 0} \text{e}^{-a}=\text{e}^0=1$
$\lim\limits_{a \to 0^+} -\dfrac{1}{a}=-\infty$ et $\lim\limits_{x \to -\infty} \text{e}^x=0$. Donc $\lim\limits_{a \to 0^+} \text{e}^{-1/a}=0$.
Par conséquent :
$\begin{align*} \displaystyle \lim\limits_{a \to 0^+} \int_a^1 \left(f(x)-g(x)\right)\text{d} x&=1+0-\text{e}^{-1}-\text{e}^{-1} \\
&=1-2\text{e}^{-1}\end{align*}$
$\quad$
4. On admet que \[\displaystyle\lim_{a\to 0} \displaystyle\int_{a}^{1} \left ( f(x)-g(x)\strut\right ) \text{d} x =\displaystyle\lim_{b\to +\infty} \displaystyle\int_{1}^{b} \left ( g(x)-f(x)\strut\right ) \text{d} x .\] Interpréter graphiquement cette égalité.
Cette égalité signifie que l’aire du domaine compris entre $\mathscr{C}_f$, $\mathscr{C}_g$ et les droites d’équation $x=0$ et $x=1$ est égale à celle du domaine compris entre $\mathscr{C}_g$ et  $\mathscr{C}_f$ pour tous les points dont l’abscisse est supérieure à $1$.
$\quad$