Baccalauréat S Centres étrangers 13 juin 2017 - Correction Exercice 4
Correction de l'exercice 4 5 points
Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. Pour tout entier $n \geqslant 4$, on considère $P_n$ un polygone régulier à $n$ côtés, de centre O et dont l'aire est égale à 1. On admet qu'un tel polygone est constitué de $n$ triangles superposables à un triangle OA$_n$B$_n$ donné, isocèle en O. On note $r_n = \text{OA}_n$ la distance entre le centre O et le sommet A$_n$ d'un tel polygone.
Partie A : étude du cas particulier $n = 6$
On a représenté ci-dessous un polygone $P_6$. 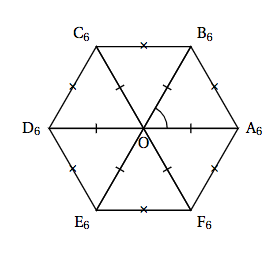
- Justifier le fait que le triangle OA$_6$B$_6$ est équilatéral, et que son aire est égale à $\dfrac{1}{6}$. Les angles au centre sont tous égaux et mesurent $\dfrac{360}{6}=60$°.
- Exprimer en fonction de $r_6$ la hauteur du triangle OA$_6$B$_6$ issue du sommet B$_6$. On appelle $M$ le milieu de $\left[OA_6\right]$.
- En déduire que $r_6 = \sqrt{\dfrac{2}{3\sqrt{3}}}$. L’aire du triangle $OA_6B_6$ est donc également $\begin{align*} \mathscr{A}_6&= \dfrac{r_6\times \dfrac{r_6\sqrt{3}}{2}}{2} \\
Le triangle $OA_6B_6$ est isocèle en $O$.
Puisque l’angle au sommet principal $\widehat{A_6OB_6}$ mesure $60$° cela signifie donc que le triangle $OA_6B_6$ est équilatéral.
$\quad$
Tous les triangles étant superposables ont la même aire $\mathscr{A}_6$. On sait également que l’aire du polygone est égale à $1$.
Ainsi $6\times \mathscr{A}_6=1$ soit $\mathscr{A}_6=\dfrac{1}{6}$.
$\quad$
Puisque le triangle $OA_6B_6$ est équilatéral, cela signifie que la hauteur $\left(B_6M\right)$ est également une médiane.
Ainsi $OM=\dfrac{r_6}{2}$.
On applique alors le théorème de Pythagore dans le triangle $OMB_6$ rectangle en $M$ :
$\begin{align*} {OB_6}^2=OM^2+{MB_6}^2 &\iff {r_6}^2=\dfrac{{r_6}^2}{4}+{MB_6}^2 \\
&\iff {MB_6}^2=\dfrac{3{r_6}^2}{4} \\
&\iff MB_6=\dfrac{r_6\sqrt{3}}{2}
\end{align*}$
$\quad$
&=\dfrac{{r_6}^2\sqrt{3}}{4}
\end{align*}$
Cela signifie donc que :
$\begin{align*} \dfrac{{r_6}^2\sqrt{3}}{4}=\dfrac{1}{6}&\iff {r_6}^2=\dfrac{4}{6\sqrt{3}} \\
&\iff {r_6}^2=\dfrac{2}{3\sqrt{3}} \\
&\iff r_6=\sqrt{\dfrac{2}{3\sqrt{3}}}
\end{align*}$
$\quad$
Partie B : cas général avec $n \geqslant 4$
Dans cette partie, on considère le polygone $P_n$ avec $n \geqslant 4$, construit de telle sorte que le point A$_n$ soit situé sur l'axe réel, et ait pour affixe $r_n$. On note alors $r_n \mathrm{e}^{\text{i}\theta_n}$ l’affixe de B$_n$ où $\theta_n$ est un réel de l'intervalle $\left]0~;~\dfrac{\pi}{2}\right]$. 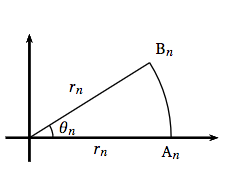
- Exprimer en fonction de $r_n$ et $\theta_n$ la hauteur issue de B$_n$ dans le triangle OA$_n$B$_n$ puis établir que l'aire de ce triangle est égale à $\dfrac{r_n^2}{2} \sin \left(\theta_n \right)$. On appelle $M$ le pied de la hauteur issue de $B_n$.
- On rappelle que l'aire du polygone $P_n$ est égale à 1. Donner, en fonction de $n$, une mesure de l'angle $\left(\vec{\text{OA}_n},~\vec{\text{OB}_n}\right)$, puis démontrer que : \[r_n = \sqrt{\dfrac{2}{n \sin \left(\dfrac{2\pi}{n}\right)}}.\] Les $n$ angles au centre ont tous la même mesure. Ainsi :
Dans le triangle $OMB_n$ rectangle en $M$ on a :
$\begin{align*}\sin\left(\theta_n\right)=\dfrac{OM}{OB_n} &\iff \sin\left(\theta_n\right)=\dfrac{OM}{r_n} \\
&\iff OM=r_n\sin\left(\theta_n\right)
\end{align*}$
$\quad$
Remarque : On pouvait également voir la hauteur $MB_n$ comme (la valeur absolue de ) la partie imaginaire de l’affixe de $B_n$ qui est $r_n\text{e}^{\text{i} \theta_n}=r_n\left(\cos \left(\theta_n\right)+\text{i} \sin \left(\theta_n\right)\right)$.
$\quad$
L’aire du triangle $OA_nB_n$ est :
$\begin{align*} \mathscr{A}_n&=\dfrac{OA_n\times MB_n}{2} \\
&=\dfrac{r_n\times r_n\sin \theta_n}{2} \\
&=\dfrac{{r_n}^2}{2}\sin\left(\theta_n\right)
\end{align*}$
$\quad$
$\begin{align*} \left(\vec{OA_n},\vec{OB_n}\right)&=\theta_n \\
&=\dfrac{2\pi}{n}
\end{align*}$
$\quad$
On sait que l’aire du polygone $P_n$ est égale à $1$.
Par conséquent :
$\begin{align*} n\times \mathscr{A}_n=1 &\iff \dfrac{n{r_n}^2}{2}\sin\left(\dfrac{2\pi}{n}\right)=1 \\
&\iff {r_n}^2=\dfrac{2}{n\sin\left(\dfrac{2\pi}{n}\right)} \\
&\iff r_n=\sqrt{\dfrac{2}{n\sin\left(\dfrac{2\pi}{n}\right)}}
\end{align*}$
$\quad$
Partie C : étude de la suite $\left(r_n\right)$
On considère la fonction $f$ définie pour tout réel $x$ de l'intervalle $]0~;~\pi[$ par \[f(x) = \dfrac{x}{\sin x}.\] Ainsi, le nombre $r_n$, défini dans la partie B pour $n \geqslant 4$, s'exprime à l'aide de la fonction $f$ par : \[r_n=\sqrt{\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n}\right)}.\] On admet que la fonction $f$ est strictement croissante sur l'intervalle $]0~;~\pi[$.
- Montrer que la suite $\left(r_n\right)$ est décroissante. On pourra pour cela commencer par démontrer que pour tout $n \geqslant 4$, on a : $0 < \dfrac{2\pi}{n+1} < \dfrac{2\pi}{n} < \pi$. Pour tout entier naturel $n\geq 4$ on a :
- En déduire que la suite $\left(r_n\right)$ converge. On ne demande pas de déterminer sa limite $L$, et on admet dans la suite de l'exercice que $L = \dfrac{1}{\sqrt{\pi}}$. La suite $\left(r_n\right)$ est donc décroissante et minorée par $0$. Elle converge donc.
- On considère l'algorithme suivant. $$\begin{array}{|l |l |}\hline \text{VARIABLES: } & n \text{ est un nombre entier }\\ \text{ TRAITEMENT : }& n \text{ prend la valeur 4 }\\ &\text{Tant que } \sqrt{\dfrac{2}{n \sin \left(\dfrac{2\pi}{n}\right)}}> 0,58 \text{ faire }\\ &\hspace{1cm} n \text{ prend la valeur }n + 1 \\ &\text{ Fin Tant que }\\ \text{SORTIE : } &\text{Afficher }n \\ \hline \end{array}$$ Quelle valeur numérique de $n$ va afficher en sortie cet algorithme ? L’algorithme renvoie le plus petit entier naturel $n$ tel que $r_n\leq 0,58$.
$\begin{align*} 0<2<n<n+1&\iff 0<\dfrac{1}{n+1}<\dfrac{1}{n}<\dfrac{1}{2} \\
&\iff 0 < \dfrac{2\pi}{n+1}<\dfrac{2\pi}{n}<\pi \\
&\iff 0<f\left(\dfrac{2\pi}{n+1}\right)<f\left(\dfrac{2\pi}{n}\right) \quad (*)\\
&\iff 0<\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n+1}\right)<\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n}\right) \\
&\iff 0<\sqrt{\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n+1}\right)}<\sqrt{\dfrac{1}{\pi}f\left(\dfrac{2\pi}{n}\right) } \quad (**)\\
&\iff 0<r_{n+1}<r_n
\end{align*}$
$\quad$
$(*)$ car la fonction $f$ est croissante et strictement positive (quotient de fonctions strictement positives sur l’intervalle d’étude) sur l’intervalle $]0;\pi[$.
$(**)$ car la fonction racine carré est croissante sur l’intervalle $[0;+\infty[$.$\quad$
La suite $\left(r_n\right)$ est donc décroissante.
$\quad$
$\quad$
La suite $\left(r_n\right)$ est décroissante.
D’après la calculatrice $r_{10} \approx 0,583~318$ et $r_{11}\approx 0,579~915$
L’algorithme va donc afficher $11$.
$\quad$
- Vues: 38351
