Baccalauréat S Centres étrangers 13 juin 2017 - Correction Exercice 1
Correction de l'exercice 1 (5 points)
Cet exercice est un questionnaire à choix multiples (Q.C.M.).
Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse exacte.
Aucune justification n'est demandée. Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapportent aucun point.
On étudie la production d'une usine qui fabrique des bonbons, conditionnés en sachets.
On choisit un sachet au hasard dans la production journalière. La masse de ce sachet, exprimée en gramme, est modélisée par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 175$. De plus, une observation statistique a montré que 2% des sachets ont une masse inférieure ou égale à 170 g, ce qui se traduit dans le modèle considéré par : $P(X \leqslant 170) = 0,02$.
- Quelle est la probabilité, arrondie au centième, de l'évènement « la masse du sachet est comprise entre 170 et 180 grammes» ?
- A. 0,04
- B. 0,96
- C. 0,98
- D. On ne peut pas répondre car il manque des données.
On appelle $\sigma$ l’écart-type associé à la variable aléatoire $X$. - Les différents bonbons présents dans les sachets sont tous enrobés d'une couche de cire comestible. Ce procédé, qui déforme certains bonbons, est effectué par deux machines A et B. Lorsqu'il est produit par la machine A, la probabilité qu'un bonbon prélevé aléatoirement soit déformé est égale à $0,05$.
Sur un échantillon aléatoire de 50 bonbons issus de la machine A, quelle est la probabilité, arrondie au centième, qu'au moins 2 bonbons soient déformés ?
- A.0,72
- B. 0,28
- C.0,54
- D. On ne peut pas répondre car il manque des données
On appelle $B$ la variable aléatoire comptant le nombre de bonbons déformés. - La machine A produit un tiers des bonbons de l'usine. Le reste de la production est assuré par la machine B. Lorsqu'il est produit par la machine B, la probabilité qu'un bonbon prélevé aléatoirement soit déformé est égale à $0,02$. Dans un test de contrôle, on prélève au hasard un bonbon dans l'ensemble de la production. Celui-ci est déformé.
Quelle est la probabilité, arrondie au centième, qu'il soit produit par la machine B ?- A. 0,02
- B. 0,67
- C. 0,44
- D. 0,01
On considère les événements suivants : - La durée de vie de fonctionnement, exprimée en jour, d'une machine servant à l'enrobage, est modélisée par une variable aléatoire $Y$ qui suit la loi exponentielle dont l'espérance est égale à 500 jours.
Quelle est la probabilité, arrondie au centième, que la durée de fonctionnement de la machine soit inférieure ou égale à 300 jours ?
- A. 0,45
- B. 1
- C.0,55
- D.On ne peut pas répondre car il manque des données
La variable aléatoire $Y$ suit la loi exponentielle de paramètre $\lambda$. - L'entreprise souhaite estimer la proportion de personnes de plus de 20 ans parmi ses clients, au niveau de confiance de 95%, avec un intervalle d'amplitude inférieure à $0,05$. Elle interroge pour cela un échantillon aléatoire de clients.
Quel est le nombre minimal de clients à interroger ?
- A.40
- B. 400
- C.1600
- D.20
Un intervalle de confiance au niveau de confiance de $95\%$ est du type $\left[f-\dfrac{1}{\sqrt{n}};f+\dfrac{1}{\sqrt{n}}\right]$.
$\begin{align*} P(X \leq 170)=0,02 &\iff P(X-175 \leq -5)=0,02 \\
P(\left(\dfrac{X-175}{\sigma} \leq -\dfrac{5}{\sigma}\right)=0,02
\end{align*}$
La variable aléatoire $X’=\dfrac{X-175}{\sigma}$ suit la loi normale centrée réduite et on a donc $P(\left(X’ \leq -\dfrac{0,05}{\sigma}\right)=0,02$.
En utilisant la touche inverse loi normale de la calculatrice on trouve $-\dfrac{5}{\sigma}\approx -2,054$.
Soit $\sigma \approx 2,434$.
On en déduit donc que $P(170\leq X\leq 180) \approx 0,96$.
Réponse B
$\quad$
Remarque : Il y avait beaucoup plus rapide en voyant que :
$\begin{align*} P(170\leq X\leq 180)&=2P(170\leq X\leq 175) \\
&=2\left(0,5-P(X \leq 170)\right)\\
&=2(0,5-0,02) \\
&=0,96
\end{align*}$
$\quad$
Il y a $50$ tirages aléatoires, indépendants et identiques (on suppose le nombre de bonbons suffisamment important pour que ce soit le cas). A chaque tirage, il n’y a que $2$ issues : le bonbon est déformé ou ne l’est pas. La probabilité qu’il soit déformé est $0,05$.
La variable aléatoire $B$ suit donc la loi binomiale de paramètres $n=50$ et$ p=0,05$.
On veut calculer $P(B\geq 2) = 1-P(B\leq 1) \approx 0,72$ (d’après la calculatrice).
Réponse A
$\quad$
– $A$ : le bonbon est produit par la machine A;
– $B$ : le bonbon est produit par la machine B;
– $D$ : le bonbon est déformé.
On obtient l’arbre pondéré suivant :
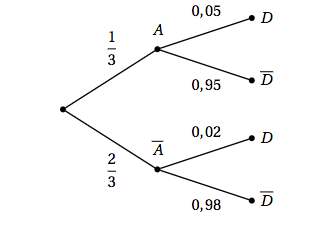
D’après la formule des probabilités totales on a :
$\begin{align*} p(D)&=p(A\cap D)+p(B \cap D) \\
&=\dfrac{1}{3}\times 0,05+\dfrac{2}{3}\times 0,02 \\
&=0,03
\end{align*}$
On veut calculer :
$\begin{align*} p_D(B)&=\dfrac{p(D\cap B)}{p(D)} \\
&=\dfrac{\dfrac{2}{3}\times 0,02}{0,03} \\
&\approx 0,44
\end{align*}$
Réponse C
$\quad$
On a $E(Y)=\dfrac{1}{\lambda} \iff 500=\dfrac{1}{\lambda} \iff \lambda=\dfrac{1}{500}$ $\iff \lambda =0,002$.
On veut calculer $P(Y\leq 300) =1-\text{e}^{-0,002\times 300}\approx 0,45$.
Réponse A
$\quad$
Son amplitude est donc égale à $\dfrac{2}{\sqrt{n}}$.
Par conséquent :
$\begin{align*} \dfrac{2}{\sqrt{n}}=0,05&\iff \sqrt{n}=\dfrac{2}{0,05} \\
&\iff \sqrt{n}=40 \\
&\iff n=1~600
\end{align*}$
Réponse C
$\quad$
- Vues: 33561
