Baccalauréat S Liban 5 juin 2017
Page 1 sur 10
Exercice 1 6 points
On considère un cube ABCDEFGH dont la représentation graphique en perspective cavalière est donnée ci-dessous. Les arêtes sont de longueur 1. L'espace est rapporté au repère orthonormé $\left(\text{D};\vec{\text{DA}},\vec{\text{DC}},\vec{\text{DH}}\right)$.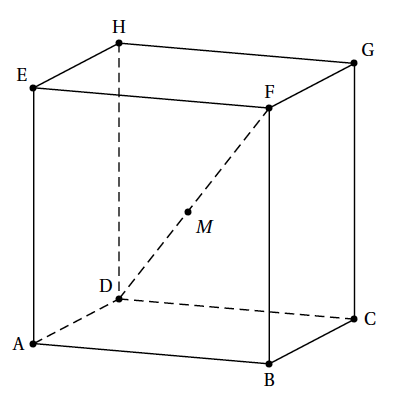
Partie A
- Montrer que le vecteur $\vec{\text{DF}}$ est normal au plan (EBG).
- Déterminer une équation cartésienne du plan (EBG).
- En déduire les coordonnées du point I intersection de la droite (DF) et du plan (EBG). On démontrerait de la même manière que le point J intersection de la droite (DF) et du plan (AHC) a pour coordonnées $\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3} \right)$.
Partie B
À tout réel $x$ de l'intervalle [0;1], on associe le point $M$ du segment [DF] tel que $\vec{\text{D}M} = x\vec{\text{DF}}$. On s'intéresse à l'évolution de la mesure $\theta$ en radian de l'angle $\widehat{\text{EMB}}$ lorsque le point $M$ parcourt le segment [DF]. On a $0 \leqslant \theta \leqslant \pi$.
- Que vaut $\theta$ si le point $M$ est confondu avec le point D ? avec le point F ?
-
- Justifier que les coordonnées du point $M$ sont $(x;x;x)$.
- Montrer que $\cos (\theta) = \dfrac{3x^2 - 4x + 1}{3x^2 - 4x + 2}$. On pourra pour cela s'intéresser au produit scalaire des vecteurs $\vec{M\text{E}}$ et $\vec{M\text{B}}$.
- On a construit ci-dessous le tableau de variations de la fonction \[f \::\: x \longmapsto \dfrac{3x^2 - 4x + 1}{3x^2 - 4x + 2}.\]
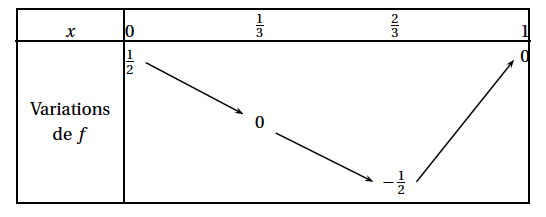
Pour quelles positions du point $M$ sur le segment [DF] :- le triangle $M$EB est-il rectangle en $M$ ?
- l'angle $\theta$ est-il maximal ?
- Vues: 35304
