Baccalauréat S Amérique du Nord 2 juin 2017 - Correction Exercice 2
Correction de l'exercice 2 (5 points)
Un fabricant doit réaliser un portail en bois plein sur mesure pour un particulier. L'ouverture du mur d'enceinte (non encore construit) ne peut excéder 4 mètres de large. Le portail est constitué de deux vantaux de largeur $a$ telle que $0 < a \leqslant 2$.
Dans le modèle choisi, le portail fermé a la forme illustrée par la figure ci-dessous. Les côtés [AD] et [BC] sont perpendiculaires au seuil [CD] du portail. Entre les points A et B, le haut des vantaux a la forme d'une portion de courbe.
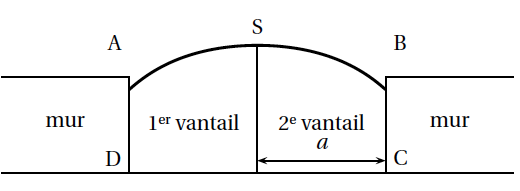
Cette portion de courbe est une partie de la représentation graphique de la fonction $f$ définie sur $[-2;2]$ par: \[f(x) = - \dfrac{b}{8}\left(\text{e}^{\frac{x}{b}} + \text{e}^{-\frac{x}{b}}\right) + \dfrac{9}{4} \quad \text{ où } b > 0.\] Le repère est choisi de façon que les points A, B, C et D aient pour coordonnées respectives $(-a;f( -a))$, $(a;f(a))$, $(a;0)$ et $(-a;0)$ et on note S le sommet de la courbe de $f$, comme illustré ci-dessous.
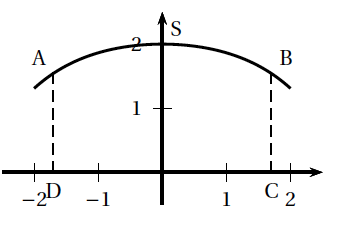
Partie A
- Montrer que, pour tout réel $x$ appartenant à l'intervalle $[-2;2]$, $f(-x) = f(x)$. Que peut-on en déduire pour la courbe représentative de la fonction $f$ ? $\begin{align*} f(-x)&=-\dfrac{b}{8}\left(\text{e}^{\frac{-x}{b}}+\text{e}^{-\frac{-x}{b}}\right)+\dfrac{9}{4} \\
- On appelle $f'$ la fonction dérivée de la fonction $f$. Montrer que, pour tout réel $x$ de l'intervalle $[-2;2]$ : \[f'(x) = - \dfrac{1}{8}\left(\text{e}^{\frac{x}{b}} + \text{e}^{-\frac{x}{b}}\right).\] La fonction $f$ est dérivable sur l’intervalle $[-2;2]$ en tant que somme de fonctions dérivables.
- Dresser le tableau de variations de la fonction $f$ sur l'intervalle $[-2;2]$ et en déduire les coordonnées du point S en fonction de $b$. Pour tout réel $x\in[0;2]$ on a, puisque $b>0$ :
&=-\dfrac{b}{8}\left(\text{e}^{\frac{-x}{b}}+\text{e}^{\frac{x}{b}}\right)+\dfrac{9}{4} \\
&=f(x)
\end{align*}$
La courbe représentative de la fonction $f$ est donc symétrique par rapport à l’axe des ordonnées.
$\quad$
$\begin{align*} f'(x)&=-\dfrac{b}{8}\left(\dfrac{1}{b}\text{e}^{\frac{x}{b}}-\dfrac{1}{b}\text{e}^{-\frac{x}{b}}\right) \\
&=-\dfrac{1}{8}\left(\text{e}^{\frac{x}{b}}-\text{e}^{-\frac{x}{b}}\right)
\end{align*}$
$\quad$
$\dfrac{x}{b}\geqslant -\dfrac{x}{b}$
$\iff \text{e}^{\frac{x}{b}} \geqslant \text{e}^{-\frac{x}{b}}$
$\iff \text{e}^{\frac{x}{b}}-\text{e}^{-\frac{x}{b}} \geqslant 0$
$\iff -\dfrac{1}{8}\left(\text{e}^{\frac{x}{b}}-\text{e}^{-\frac{x}{b}}\right) \leqslant 0$
$\iff f'(x) \leqslant 0$
La fonction $f$ est donc décroissante sur l’intervalle $[0;2]$.
Par symétrie, la fonction $f$ est donc croissante sur l’intervalle $[2;0]$.
On obtient le tableau de variation suivant :
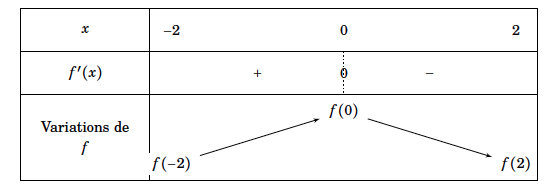
Avec $f(-2)=-\dfrac{b}{8}\left(e^{\dfrac{-2}{b}}+\text{e}^{\dfrac{2}{b}}\right)+\dfrac{9}{4}=f(2)$
Et $f(0)=-\dfrac{b}{8}\times 2+\dfrac{9}{4}=\dfrac{-b+9}{4}$.
Ainsi $S\left(0;\dfrac{-b+9}{4}\right)$.
$\quad$
Partie B
La hauteur du mur est de 1,5 m. On souhaite que le point S soit à 2 m du sol. On cherche alors les valeurs de $a$ et $b$.
- Justifier que $b = 1$. On veut que :
- Montrer que l'équation $f(x) = 1,5$ admet une unique solution sur l'intervalle $[0;2]$ et en déduire une valeur approchée de $a$ au centième. On a donc $f(x)=-\dfrac{1}{8}\left(e^x+e^{-x}\right)+\dfrac{9}{4}$.
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
- Dans cette question, on choisit $a = 1,8$ et $b = 1$. Le client décide d'automatiser son portail si la masse d'un vantail excède $60$ kg. La densité des planches de bois utilisées pour la fabrication des vantaux est égale à $20$ kg.m$^{-2}$. Que décide le client ? Calculons la surface d’un vantail.
$\begin{align*} f(0)=2&\iff \dfrac{-b+9}{4}=2 \\
&\iff -b+9=8 \\
&\iff -b=-1 \\
&\iff b=1
\end{align*}$
$\quad$
et $f(2)=-\dfrac{1}{8}\left(e^2+e^{-2}\right)+\dfrac{9}{4}\approx 1,309$
$\6$ est compris entre $\5$ et $\4$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right]$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right) > \8 > \3\left(\6\right)$, soit $\3\left(\4\right)> \3\left(\1\right)>\3\left(\6\right)$
comme $\3$ est strictement décroissante sur $\left[\9;\10\right]$; on déduit $\4< \1 < \6$
L’équation $f(x)=1,5$ possède une unique solution dont une valeur approchée est $1,76$.
Ainsi $a\approx 1,76$.
$\quad$
Il s’agit de l’aire comprise entre l’axe des abscisses, la courbe représentant la fonction $f$ et les droites d’équation $x=0$ et $ x=1,8$.
Puisque la fonction $f$ est positive sur l’intervalle $[0;1,8]$ (le minimum est $1,5$ d’après ce qui a été dit à la question précédente) l’aire cherchée est :
$\begin{align*} \mathscr{A}&=\int_0^{1,8}f(x) dx \phantom{\dfrac{1}{1}} \\
&=\left[-\dfrac{1}{8}\left[e^x-e^{-x}\right]+\dfrac{9}{4}x\right]_0^{1,8} \\
&=-\dfrac{1}{8}\left(e^{1,8}-\text{e}^{-1,8}\right)+\dfrac{9}{4}\times 1,8-0\\
&\approx 3,314
\end{align*}$
La masse du vantail est donc :
$M=20\times \mathscr{A}\approx 66,289>60$
Le client décidera donc d’automatiser son portail.
$\quad$
Partie C
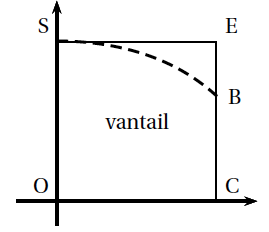
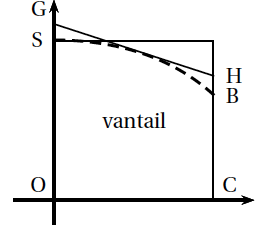
On conserve les valeurs $a = 1,8$ et $b = 1$. Pour découper les vantaux, le fabricant prédécoupe des planches. Il a le choix entre deux formes de planches prédécoupées : soit un rectangle OCES, soit un trapèze OCHG comme dans les schémas ci-dessous. Dans la deuxième méthode, la droite (GH) est la tangente à la courbe représentative de la fonction $f$ au point F d'abscisse $1$.
|
|
| Forme 1 : découpe dans un rectangle | Forme 2 : découpe dans un trapèze |
La forme 1 est la plus simple, mais visuellement la forme 2 semble plus économique. Évaluer l'économie réalisée en termes de surface de bois en choisissant la forme 2 plutôt que la forme 1.
On rappelle la formule donnant l'aire d'un trapèze. En notant $b$ et $B$ respectivement les longueurs de la petite base et de la grande base du trapèze (côtés parallèles) et $h$ la hauteur du trapèze : \[\text{Aire } = \dfrac{b+B}{2} \times h.\]
Avec la forme 1
Le rectangle a donc pour dimension $1,8\times 2$
L’aire de partie perdue est :
$\mathscr{A}_1=2\times 1,8-\mathscr{A}\approx 0,286$
$\quad$
Avec la forme 2
$f'(1)=-\dfrac{1}{8}\left(\text{e}-\text{e}^{-1}\right)$ et $f(1)=-\dfrac{1}{8}\left(\text{e}+\text{e}^{-1}\right)+\dfrac{9}{4}$
Une équation de la tangente $T$ au point $F$ est $y=f'(1)(x-1)+f(1)$
L’ordonnée à l’origine est donc
$\begin{align*} -f'(1)+f(1)&=\dfrac{1}{8}\left(\text{e}-\text{e}^{-1}\right)-\dfrac{1}{8}\left(\text{e}+\text{e}^{-1}\right)+\dfrac{9}{4} \\
&=-2\times \dfrac{1}{8}e^{-1}+\dfrac{9}{4} \\
&=\dfrac{-\text{e}^{-1}+9}{4}
\end{align*}$
Le point de la tangente $T$ ayant pour abscisse $1,8$ a pour ordonnée :
$\begin{align*} y&=f'(1)\times (1,8-1)+f(1) \\
&=f'(1)\times 0,8+f(1) \\
&=-0,1\left(\text{e}-\text{e}^{-1}\right)-\dfrac{1}{8}\left(\text{e}+\text{e}^{-1}\right)+\dfrac{9}{4}
\end{align*}$
Ainsi l’aire du trapèze est :
$\mathscr{A}_T=\dfrac{\dfrac{-\text{e}^{-1}+9}{4}-0,1\left(\text{e}-\text{e}^{-1}\right)-\dfrac{1}{8}\left(\text{e}+\text{e}^{-1}\right)+\dfrac{9}{4} }{2}\times 1,8 $
L’aire de la partie perdue est $\mathscr{A_2}=\mathscr{A}_T-\mathscr{A}\approx 0,094$
Par conséquent on économise environ $0,286-0,094= 0,191$ m$^2$ de bois en choisissant la forme 2.
- Vues: 17510
