Baccalauréat S Amérique du Nord 2 juin 2017 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 5 points

Commun à tous les candidats

Un fabricant doit réaliser un portail en bois plein sur mesure pour un particulier. L'ouverture du mur d'enceinte (non encore construit) ne peut excéder 4 mètres de large. Le portail est constitué de deux vantaux de largeur $a$ telle que $0 < a \leqslant 2$.
Dans le modèle choisi, le portail fermé a la forme illustrée par la figure ci-dessous. Les côtés [AD] et [BC] sont perpendiculaires au seuil [CD] du portail. Entre les points A et B, le haut des vantaux a la forme d'une portion de courbe.

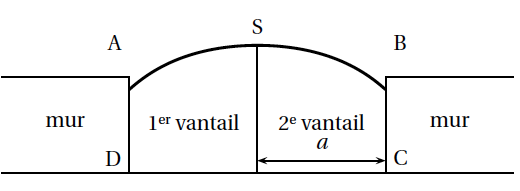
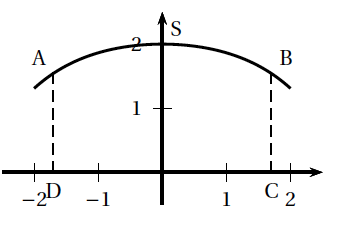
Cette portion de courbe est une partie de la représentation graphique de la fonction $f$ définie sur $[-2;2]$ par: \[f(x) = - \dfrac{b}{8}\left(\text{e}^{\frac{x}{b}} + \text{e}^{-\frac{x}{b}}\right) + \dfrac{9}{4} \quad \text{ où } b > 0.\] Le repère est choisi de façon que les points A, B, C et D aient pour coordonnées respectives $(-a;f( -a))$, $(a;f(a))$, $(a;0)$ et $(-a;0)$ et on note S le sommet de la courbe de $f$, comme illustré ci-dessous.

 

Partie A

 

1. Montrer que, pour tout réel $x$ appartenant à l'intervalle $[-2;2]$, $f(-x) = f(x)$. Que peut-on en déduire pour la courbe représentative de la fonction $f$ ?
2. On appelle $f'$ la fonction dérivée de la fonction $f$. Montrer que, pour tout réel $x$ de l'intervalle $[-2;2]$ : \[f'(x) = - \dfrac{1}{8}\left(\text{e}^{\frac{x}{b}} + \text{e}^{-\frac{x}{b}}\right).\]
3. Dresser le tableau de variations de la fonction $f$ sur l'intervalle $[-2;2]$ et en déduire les coordonnées du point S en fonction de $b$.

Partie B

La hauteur du mur est de 1,5 m. On souhaite que le point S soit à 2 m du sol. On cherche alors les valeurs de $a$ et $b$.

1. Justifier que $b = 1$.
2. Montrer que l'équation $f(x) = 1,5$ admet une unique solution sur l'intervalle $[0;2]$ et en déduire une valeur approchée de $a$ au centième.
3. Dans cette question, on choisit $a = 1,8$ et $b = 1$. Le client décide d'automatiser son portail si la masse d'un vantail excède $60$ kg. La densité des planches de bois utilisées pour la fabrication des vantaux est égale à $20$ kg.m$^{-2}$. Que décide le client ?

Partie C

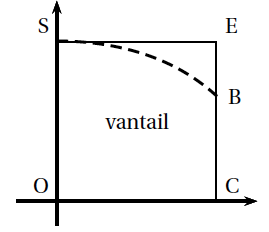
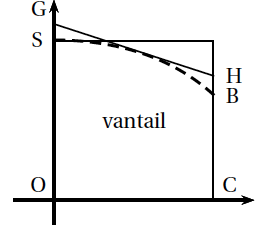
On conserve les valeurs $a = 1,8$ et $b = 1$. Pour découper les vantaux, le fabricant prédécoupe des planches. Il a le choix entre deux formes de planches prédécoupées : soit un rectangle OCES, soit un trapèze OCHG comme dans les schémas ci-dessous. Dans la deuxième méthode, la droite (GH) est la tangente à la courbe représentative de la fonction $f$ au point F d'abscisse $1$.

Forme 1 : découpe dans un rectangle	Forme 2 : découpe dans un trapèze

La forme 1 est la plus simple, mais visuellement la forme 2 semble plus économique. Évaluer l'économie réalisée en termes de surface de bois en choisissant la forme 2 plutôt que la forme 1.
On rappelle la formule donnant l'aire d'un trapèze. En notant $b$ et $B$ respectivement les longueurs de la petite base et de la grande base du trapèze (côtés parallèles) et $h$ la hauteur du trapèze : \[\text{Aire } = \dfrac{b+B}{2} \times h.\]