Baccalauréat S Métropole 21 juin 2017 - Correction Exercice 4
Correction de l'exercice 4 5 points
On étudie un modèle de propagation d'un virus dans une population, semaine après semaine. Chaque individu de la population peut être, à l'exclusion de toute autre possibilité :
- soit susceptible d'être atteint par le virus, on dira qu'il est « de type S»;
- soit malade (atteint par le virus) ;
- soit immunisé (ne peut plus être atteint par le virus).
Un individu est immunisé lorsqu'il a été vacciné, ou lorsqu'il a guéri après avoir été atteint par le virus.
Pour tout entier naturel $n$, le modèle de propagation du virus est défini par les règles suivantes :
- Parmi les individus de type S en semaine $n$, on observe qu'en semaine $n + 1$ : 85 % restent de type S, 5 % deviennent malades et 10 % deviennent immunisés ;
- Parmi les individus malades en semaine $n$, on observe qu'en semaine $n + 1$ : 65 % restent malades, et 35 % sont guéris et deviennent immunisés.
- Tout individu immunisé en semaine $n$ reste immunisé en semaine $n + 1$.
On choisit au hasard un individu dans la population. On considère les événements suivants : $S_n$ : « l'individu est de type S en semaine $n$»;
$M_n$ : « l'individu est malade en semaine $n$»;
$I_n$ : « l'individu est immunisé en semaine $n$».
En semaine 0, tous les individus sont considérés « de type S », on a donc les probabilités suivantes : \[P\left(S_0\right) = 1~;~P\left(M_0\right) = 0\text{ et }P\left(I_0\right) = 0. \]
Partie A
On étudie l'évolution de l'épidémie au cours des semaines 1 et 2.
- Reproduire sur la copie et compléter l'arbre de probabilités donné ci-dessous :
 On obtient l’arbre de probabilités suivant :
On obtient l’arbre de probabilités suivant : - Montrer que $P\left(I_2\right)= 0,2025$. D’après la formule des probabilités totales on a :
- Sachant qu'un individu est immunisé en semaine 2, quelle est la probabilité, arrondie au millième, qu'il ait été malade en semaine 1 ? On veut calculer :
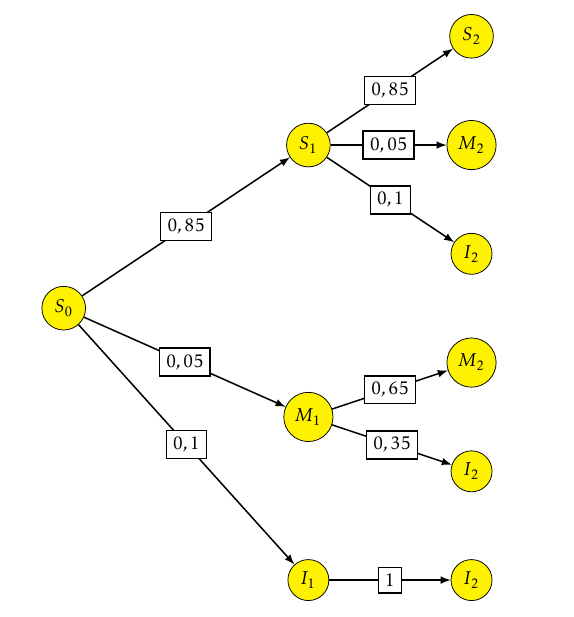
$\begin{align*} P\left(I_2\right)&=P\left(S_1\cap I_2\right)+P\left(M_1\cap I_2\right)+P\left(I_1\cap I_2\right) \\
&=0,85\times 0,1+0,05\times 0,35+0,1\times 1 \\
&=0,202~5
\end{align*}$
$\quad$
$\begin{align*} P_{I_2}\left(M_1\right)&=\dfrac{P\left(I_2\cap M_1\right)}{P\left(I_2\right)} \\
&=\dfrac{0,05\times 0,35}{0,202~5} \\
&=\dfrac{7}{81}\\
&\approx 0,086\\
\end{align*}$
$\quad$
PARTIE B
On étudie à long terme l'évolution de la maladie. Pour tout entier naturel $n$, on : $u_n=P\left(S_n\right)$, $v_n=p\left(M_n\right)$ et $w_n=P\left(I_n\right)$ les probabilités respectives des événements $S_n$, $M_n$ et $I_n$.
- Justifier que, pour tout entier naturel $n$, on a : $u_n+v_n+w_n=1$. On admet que la suite $\left(v_n\right)$ est définie par $v_0=0,65v_n+0,05u_n$. Chaque semaine, l’individu est soit de type $S$, soit malade ou soit immunisé.
- À l'aide d'un tableur, on a calculé les premiers termes des suites $\left(u_n\right)$, $\left(v_n\right)$ et $\left(w_n\right)$. $$\begin{array}{|c|c|c|c|c|}\hline &A&B&C&D\\ \hline 1&n&u_n&v_n&w_n\\ \hline 2&0&1&0&0\\ \hline 3&1&0,8500&0,0500&0,1000\\ \hline 4&2&0,7225&0,0750&0,2025\\ \hline 5&3&0,6141&0,0849&0,3010\\ \hline 6&4&0,5220&0,0859&0,3921\\ \hline 7&5&0,4437&0,0819&0,4744\\ \hline 8&6&0,3771&0,0754&0,5474\\ \hline \dots&\dots&\dots&\dots\\ \hline 20&18&0,0536&0,0133&0,9330\\ \hline 21&19&0,0456&0,0113&0,9431\\ \hline 22&20&0,0388&0,0096&0,9516\\ \hline \end{array} $$
Pour répondre aux questions a. et b. suivantes, on utilisera la feuille de cacul reproduite ci-dessus.- Quelle formule, saisie dans la cellule C3, permet par recopie vers le bas, de calculer les termes de la suite $\left(v_n \right)$ ? On a pu saisir en $C3$ la formule $=0,65*C2+0,05*B2$
- On admet que les termes de $\left(v_n\right)$ augmentent, puis diminuent à partir d'une certain rang $N$, appelé le « pic épidémique»: c'est l'indice de la semaine pendant laquelle la probabilité d'être malade pour un individu choisi au hasard est la plus grande. Déterminer la valeur du pic épidémique prévue par ce modèle. D’après la feuille de calcul on a :
$\quad$
$v_3=0,0849$, $v_4=0,0859$ et $v_5=0,0819$
Le pic épidémique est donc $4$.
$\quad$ -
- Justifier que, pour tout entier naturel $n$, on a : $u_{n+1}=0,85u_n$. En déduire l'expression de $u_n$ en fonction de $n$. D’après l’énoncé, parmi les individus de type $S$ en semaine $n$ on observe, qu’en semaine $n+1$, $85\%$ restent de type $S$.
- Montrer, à l'aide d'un raisonnement par récurrence, que pour tout entier naturel $n$, \[u_n=\dfrac{1}{4}\left(0,85^n-0,65^n\right).\]
Par conséquent $u_{n+1}=0,85u_n$.
La suite $\left(u_n\right)$ est donc géométrique de raison $0,85$ et de premier terme $u_0=1$.
Ainsi, pour tout entier naturel $n$, on a $u_n=0,85^n$.
$\quad$
Initialisation : Si $n=0$ on a $v_0=0$ et $\dfrac{1}{4}\left(0,85^0-0,65^0\right)=0$ - Calculer les limites de chacune des suites $\left(u_n\right)$, $\left(v_n\right)$ et $\left(w_n\right)$. Que peut-on en déduire quant à l'évolution de l'épidémie prévue à long terme par ce modèle ? $-1<0,85<1$ donc $\lim\limits_{n \to +\infty} 0,85^n =0$
$S_n,M_n,I_n$ forment une partition de l'univers. Donc $P\left(S_n\right)+P\left(M_n\right)+P\left(I_n\right)=1$.
Soit $u_n+v_n+w_n=1$
$\quad$
La propriété est donc vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$. $v_n=\dfrac{1}{4}\left(0,85^n-0,65^n\right)$.
$\begin{align*} v_{n+1}&=0,65v_n+0,05u_n \\
&=0,65\times \dfrac{1}{4}\left(0,85^n-0,65^n\right)+0,05\times 0,85^n \\
&=\dfrac{1}{4}\left(0,65\times 0,85^n-0,65^{n+1}\right)+0,05\times 0,85^n \\
&=\dfrac{1}{4}\times 0,65\times 0,85^n-\dfrac{1}{4}\times 0,65^{n+1}+0,05\times 0,85^n \\
&=\left(\dfrac{1}{4}\times 0,65+0,05\right)\times 0,85^n-\dfrac{1}{4}\times0,65^{n+1} \\
&=\dfrac{1}{4}(0,65+0,2)\times 0,85^n-\dfrac{1}{4}\times0,65^{n+1} \\
&=\dfrac{1}{4}\left(0,85^{n+1}-0,65^{n+1}\right)
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $v_n=\dfrac{1}{4}\left(0,85^n-0,65^n\right)$
$\quad$
$-1<0,65<1$ donc $\lim\limits_{n \to +\infty} 0,65^n =0$
Ainsi $\lim\limits_{n \to +\infty} u_n=0$ et $\lim\limits_{n \to +\infty} v_n=0$.
D’après la question 1. on a $u_n+v_n+w_n=1$ pour tout entier naturel $n$.
Donc $\lim\limits_{n \to +\infty} w_n=1$
Cela signifie donc que sur le long terme, selon ce modèle, tous les individus seront immunisés.
- Vues: 17721
