Baccalauréat S Métropole 21 juin 2017 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Dans une vaste plaine, un réseau de capteurs permet de détecter la foudre et de produire une image des phénomènes orageux. Ces données servent en particulier aux services météorologiques pour améliorer leurs prévisions et pour permettre des interventions plus rapides sur les lieux, notamment en cas d'incendie.
Le but de l'exercice est d'étudier les impacts de foudre détectés par un capteur. L'écran radar, sur lequel les points d'impact de foudre sont observés, a l'allure suivante :

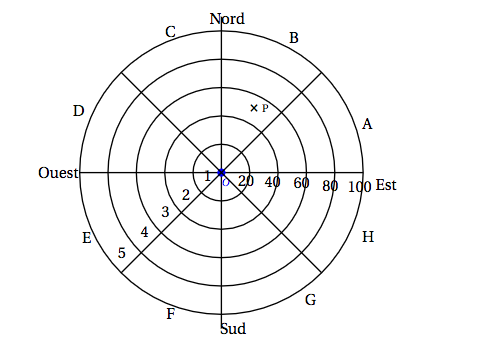
Le capteur de foudre étant représenté par le centre de l'écran, cinq cercles concentrique correspondant aux rayons respectifs 20, 40, 60, 80 et 100 kilomètres délimitent dans l'ordre cinq zones, numérotées de 1 à 5, définies par leur distance au capteur. De plus, huit segments partant du capteur délimitent huit portions, de même ouverture angulaire, nommées dans le sens trigonométrique de A à H.
L'écran est ainsi partagé en quarante secteurs dénommés par une lettre et un nombre entre 1 et 5. Par exemple, le point P positionné sur la figure est situé dans le secteur B3.
On assimile l'écran radar à une partie du plan complexe en définissant un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$ de la manière suivante :

• l'origine O marque la position du capteur ;
• l'axe des abscisses est orienté d'Ouest en Est ;
• l'axe des ordonnées est orienté du Sud au Nord ;
• l'unité choisie est le kilomètre.

Dans la suite, un point de l'écran radar est associé à un point d'affixe z.

PARTIE A

1. On note $z_P$ l'affixe du point P situé dans le secteur B3 sur le graphique précédent. On appelle $r$ le module de $z_P$ et $\theta$ son argument dans l'intervalle $]-\pi~;~\pi]$. Parmi les quatre propositions suivantes, déterminer la seule qui propose un encadrement correct pour $r$ et pour $\theta$ (aucune justification n'est demandée) : $$\begin{array}{|c|c|c|c|} \hline \text{Proposition A} & \text{Proposition B} & \text{Proposition C} &\text{Proposition D} \\ \hline 40 < r < 60 & 20 < r < 40 &40 < r < 60 & 0 < r < 60 \\ \text{et } & \text{et } & \text{et } &\text{et } \\ 0<\theta < \dfrac{\pi}{4} & \dfrac{\pi}{2}<\theta < \dfrac{3\pi}{4} & \dfrac{\pi}{4}<\theta < \dfrac{\pi}{2} & -\dfrac{\pi}{2}<\theta < -\dfrac{\pi}{4} \\ \hline \end{array} $$
Le point $P$ appartient au secteur $B3$.
Par conséquent $r=z_P\in[40;60]$ et $\theta \in \left[\dfrac{\pi}{4};\dfrac{\pi}{2}\right]$.
Proposition C

2. Un impact de foudre est matérialisé sur l'écran en un point d'affixe $z$. Dans chacun des deux cas suivants, déterminer le secteur auquel ce point appartient :
   1. $z =70\mathrm{e}^{-\mathrm{i}\frac\pi3} $ ;
   On a $z=70\text{e}^{-\text{i} \frac{\pi}{3}}$.
   Ainsi $r\in[60;80]$ et $\theta\in\left]-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right[$.
   donc le point appartient au secteur $G4$.
   $\quad$
   
   2. $z = -45\sqrt{3}+45\mathrm{i}$.
   On a $z=-45\sqrt{3}+45\text{i}$
   Donc $|z|=\sqrt{\left(-45\sqrt{3}\right)^2+45^2}=90$
   Par conséquent $z=90\left(-\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right)=90\text{e}^{\frac{5\pi}{6}}$
   Le point appartient donc au secteur $D5$.

 

Partie B

On suppose dans cette partie que le capteur affiche un impact au point P d'affixe $50\mathrm{e}^{\mathrm{i}\frac\pi3}$. En raison d'imprécisions de mesures, le point d'impact affiché ne donne qu'une indication approximative du point d'impact réel de la foudre. Ainsi, lorsque le capteur affiche le point d'impact P d'affixe $50\mathrm{e}^{\mathrm{i}\frac\pi3}$, l'affixe $z$ du point d'impact réel de la foudre admet :

• un module qui peut être modélisé par une variable aléatoire M suivant une loi normale d'espérance $\mu = 50$ et d'écart type $\sigma = 5$ ;
• un argument qui peut être modélisé par une variable aléatoire T suivant une loi normale d'espérance $\dfrac{\pi}{3}$ et d'écart type $\dfrac{\pi}{12}$.

On suppose que les variables aléatoires $M$ et $T$ sont indépendantes, c'est-à-dire que, quels que soient les intervalles $I$ et $J$, les événements $(M \in 1)$ et $(T\in J)$ sont indépendants. Dans la suite les probabilités seront arrondies à $10^{-3}$ près.

1. Calculer la probabilité $P(M < 0)$ et interpréter le résultat obtenu.

2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$

$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
D’après la calculatrice on a $P(M<0)=0,5-P(0<M<50)=0$
Cela signifie qu’il est impossible que le module du nombre complexe $z$ soit négatif ou nul.
$\quad$
2. Calculer la probabilité $P(M\in ]40~;~60[)$.

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 


D’après la calculatrice on a $P\left(M\in]40;60[\right)\approx 0,954$.
Remarque : On pouvait également dire que $P\left(M\in]40;60[\right)=P(\mu-2\sigma\leqslant M \leqslant \mu+2\sigma)$.
$\quad$
3. On admet que $P\left(T\in\left]\dfrac{\pi}{4}~;~\dfrac{\pi}{2}\right[\right)=0,819$. En déduire la probabilité que la foudre ait effectivement frappé le secteur B3 selon cette modélisation.
Les événements $(M\in I)$ et $(T\in J)$ étant indépendants on a :
$\begin{align*} P\left(\left(M\in]40;60[\right) \cap \left(T\in\left]\dfrac{\pi}{4};\dfrac{\pi}{2}\right[\right)\right) &= P\left(M\in]40;60[\right)\times P\left(T\in\left]\dfrac{\pi}{4};\dfrac{\pi}{2}\right[\right) \\
&\approx 0,954\times 0,819 \\
&\approx 0,781
\end{align*}$
$\quad$