Baccalauréat S Asie 22 juin 2017

Page 1 sur 12

 

Exercice 1 5 points

Commun à tous les candidats

Un protocole de traitement d'une maladie, chez l'enfant, comporte une perfusion longue durée d'un médicament adapté. La concentration dans le sang du médicament au cours du temps est modélisée par la fonction $C$ définie sur l'intervalle $[0~;~+ \infty[$ par : \[C(t) = \dfrac{d}{a}\left(1 - \text{e}^{-\frac{a}{80} t}\right)\] où

• $C$ désigne la concentration du médicament dans le sang, exprimée en micromole par litre,
• $t$ le temps écoulé depuis le début de la perfusion, exprimé en heure,
• $d$ le débit de la perfusion, exprimé en micromole par heure,
• $a$ un paramètre réel strictement positif, appelé clairance, exprimé en litre par heure.

Le paramètre $a$ est spécifique à chaque patient.
En médecine, on appelle « plateau » la limite en $+ \infty$ de la fonction $C$.

Partie A : étude d'un cas particulier

La clairance $a$ d'un certain patient vaut 7, et on choisit un débit $d$ égal à $84$. Dans cette partie, la fonction $C$ est donc définie sur $[0~;~+ \infty[$ par : \[C(t) = 12\left(1 - \text{e}^{-\frac{7}{80} t}\right).\]

1. Étudier le sens de variation de la fonction $C$ sur $[0~;~+ \infty[$.
2. Pour être efficace, le plateau doit être égal à 15. Le traitement de ce patient est-il efficace ?

 

Partie B : étude de fonctions

 

1. Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par : \[f(x) = \dfrac{105}{x} \left(1 - \text{e}^{- \frac{3}{40}x}\right).\] Démontrer que, pour tout réel $x$ de $]0~;~+ \infty[$, $f'(x) = \dfrac{105g(x)}{x^2}$, où $g$ est la fonction définie sur $[0~;~+ \infty[$ par : \[g(x) = \dfrac{3x}{40}\text{e}^{- \frac{3}{40}x}\ + \text{e}^{- \frac{3}{40}x} - 1.\]
2. On donne le tableau de variation de la fonction $g$ :
   
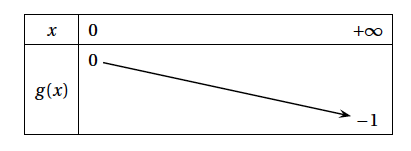
   En déduire le sens de variation de la fonction $f$.
   On ne demande pas les limites de la fonction $f$ .
3. Montrer que l'équation $f(x) = 5,9$ admet une unique solution sur l'intervalle [1 ; 80]. En déduire que cette équation admet une unique solution sur l'intervalle $]0~;~+ \infty[$. Donner une valeur approchée de cette solution au dixième près.

 

Partie C : détermination d'un traitement adéquat

Le but de cette partie est de déterminer, pour un patient donné, la valeur du débit de la perfusion qui permette au traitement d'être efficace, c'est-à-dire au plateau d'être égal à $15$. Au préalable, il faut pouvoir déterminer la clairance $a$ de ce patient. À cette fin, on règle provisoirement le débit $d$ à 105, avant de calculer le débit qui rende le traitement efficace. On rappelle que la fonction $C$ est définie sur l' intervalle $[0~;~+ \infty[$ par : \[C(t) = \dfrac{d}{a}\left(1 - \text{e}^{-\frac{a}{80} t}\right)\]

1. On cherche à déterminer la clairance a d'un patient. Le débit est provisoirement réglé à $105$.
   1. Exprimer en fonction de $a$ la concentration du médicament $6$ heures après le début de la perfusion.
   2. Au bout de $6$ heures, des analyses permettent de connaître la concentration du médicament dans le sang; elle est égale à $5,9$ micromole par litre. Déterminer une valeur approchée, au dixième de litre par heure, de la clairance de ce patient.
2. Déterminer la valeur du débit $d$ de la perfusion garantissant l'efficacité du traitement.