Baccalauréat S Métropole 21 juin 2017 - Correction Spécialité
Correction de l'exercice de Spécialité 5 points
On appelle « triangle rectangle presque isocèle » , en abrégé TRPI, un triangle rectangle dont les côtés de l'angle droit ont pour longueurs $x$ et $x + 1$, et dont l 'hypoténuse a pour longueur $y$, où $x$ et $y$ sont des entiers naturels. Ainsi, un TRPI est un triangle rectangle dont les longueurs des côtés de l'angle droit sont deux nombres entiers consécutifs et dont la longueur de l'hypoténuse est un nombre entier. 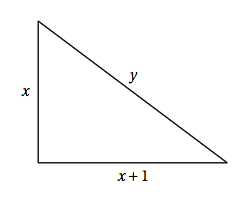
Si le triangle de côtés $x$, $x + 1$ et $y$, où $y$ est la longueur de l'hypoténuse, est un TRPI, on dira que le couple $(x~;~y)$ définit un TRPI.
Partie A
- Démontrer que le couple d'entiers naturels $(x~;~y)$ définit un TRPI si, et seulement si, on a : \[y^2 = 2x^2 + 2x + 1\] $(x;y)$ définit un TRPI
- Montrer que le TRPI ayant les plus petits côtés non nuls est défini par le couple $(3~;~5)$. Si $x=1$ alors $y^2=5$ mais $\sqrt{5}$ n’est pas un nombre entier.
-
- Soit $n$ un entier naturel. Montrer que si $n^2$ est impair alors $n$ est impair.
- Méthode 1 : Si $n$ est pair alors il existe un entier naturel $k$ tel que $n=2k$.
Par conséquent
$\begin{align*}n^2&= (2k)^2 \\
&=4k^2\\
&=2\times 2k^2
\end{align*}$
On en déduit donc que $n^2$ est également pair.
Un nombre entier pair a donc nécessairement un carré pair.
Cela signifie par conséquent que si $n^2$ est impair alors $n$ est impair.
$\quad$ - Méthode 2: on utilise la contraposée
$$\mathcal{P}\Rightarrow \mathcal{Q} \iff \text{Non}\left( \mathcal{Q}\right) \Rightarrow\text{Non}\left( \mathcal{P}\right)$$ Ici , on suppose donc que $n$ est pair et on doit prouver que $n^2$ est pair.
Or si $n$ est pair, alors $n\equiv 0\;[2]$ , d'où on déduit d'après la compatibilité des congruences avec les puissances : $n^2\equiv 0^2\;[2]$, soit $n^2\equiv 0 \;[2]$, ce qui prouve que $n^2$ est pair.
- Méthode 1 : Si $n$ est pair alors il existe un entier naturel $k$ tel que $n=2k$.
- Montrer que dans un couple d'entiers $(x~;~y)$ définissant un TRPI, le nombre $y$ est nécessairement impair. b. Si $(x;y)$ définit un TRPI alors $y^2=2x^2+2x+1$
- Montrer que si le couple d'entiers naturels $(x~;~y)$ définit un TRPI, alors $x$ et $y$ sont premiers entre eux. Si $(x;y)$ est un TRPI alors $y^2=2x^2+2x+1$
$2x^2+2x+1\equiv 1~~[2]$
Donc $y^2$ est impair.
D’après la question précédente, cela signifie donc que $y$ est impair.
$\quad$
Par conséquent :
$\begin{align*} -(2+2x)x+y\times y &= -(2+2x)x+y^2 \\
&=-2x-2x^2+2x^2+2x+1=1
\end{align*}$
D’après le théorème de Bézout, les nombres $x$ et $y$ sont premiers entre eux.
$\quad$ - Soit $n$ un entier naturel. Montrer que si $n^2$ est impair alors $n$ est impair.
$\iff y^2=x^2+(x+1)^2$ d’après le théorème de Pythagore
$\iff y^2=x^2+x^2+2x+1 $
$\iff y^2=2x^2+2x+1$
$\quad$
Si $x=2$ alors $y^2=13$ mais $\sqrt{13}$ n’est pas un nombre entier.
Si $x=3$ alors $y^2=25$. Donc $y=5$.
Le TRPI ayant les plus petits côtés non nuls est défini par le couple $(3;5)$.
$\quad$
Partie B
On note $A$ la matrice carrée : $A =\begin{pmatrix}3&2\\4&3\end{pmatrix}$, et $B$ la matrice colonne : $B=\begin{pmatrix}1\\2\end{pmatrix}$. Soient $x$ et $y$ deux entiers naturels ; on définit les entiers naturels $x'$ et $y'$ par la relation : \[\begin{pmatrix}x'\\y'\end{pmatrix} = A\begin{pmatrix}x\\y\end{pmatrix} + B.\] Exprimer $x'$ et $y'$ en fonction de $x$ et $y$.
- Montrer que : $y'^2 - 2x'(x' + 1) = y^2 - 2x(x + 1)$. On a :
- a.
$\begin{align*} {y’}^2-2x’\left(x’+1\right)&=(4x+3y+2)^2-2(3x+2y+1)(3x+2y+1+1) \\
&=16x^2+9y^2+4+24xy+16x+12y\\
&-(6x+4y+2)(3x+2y+2) \\
&=16x^2+9y^2+4+24xy+16x+12y\\
&-\left(18x^2+12xy+12x+12xy+8y^2+8y+6x+4y+4\right) \\
&=16x^2+9y^2+4+24xy+16x+12y\\
&-18x^2-24xy-18x-8y^2-12y-4 \\
&=-2x^2+y^2-2x\\
&=y^2-2x(x+1)
\end{align*}$ - En déduire que si le couple $(x~;~y)$ définit un TRPI, alors le couple $\left(x'~;~y'\right)$ définit également un TRPI. On considère les suites $\left(x_n\right)_{n\in \mathbb{N}}$ et $\left(y_n\right)_{n\in\mathbb{N}}$ d'entiers naturels, définies par $x_0 = 3$, $y_0 = 5$ et pour tout entier naturel n : $\begin{pmatrix}x_{n+1}\\ y_{n+1}\end{pmatrix}=A\begin{pmatrix}x_n\\y_n\end{pmatrix}+B$. Montrer par récurrence que, pour tout entier naturel $n$, le couple $\left(x_ny_n\right)$ définit un TRPI. ’après la question A.1. $(x;y)$ définit un TRPI si, et seulement si, $y^2=2x^2+2x+1$ soit $y^2-2x^2-2x=1$ ou encore $y^2-2x(x+1)=1$
- Initialisation : au rang $0$, on sait que le couple $(3;5)$ définit un TRPI
La propriété est donc vraie au rang $0$.
$\quad$
Initialisation : Supposons la propriété vraie au rang $n$ : $\left(x_n;y_n\right)$ définit un TRPI.
Alors $x_{n+1}=3x_n+2y_n+1$ et $y_{n+1}=4x_n+3y_n+2$
D’après la question précédente, puisque $\left(x_n;y_n\right)$ définit un TRPI, alors $\left(x_{n+1};y_{n+1}\right)$ définit également un TRPI.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ $\left(x_n;y_n\right)$ définit un TRPI.
$\quad$ - Déterminer, par la méthode de votre choix que vous préciserez, un TRPI dont les longueurs des côtés sont supérieures à 2017 En utilisant la relation matricielle on obtient successivement les couples suivant les couples suivants :
$x’=3x+2y+1$ et $y’=4x+3y+2$
$\quad$
Or ${y’}^2-2x’\left(x’+1\right)=y^2-2x(x+1)$
$(x;y)$ définit TRPI
$\iff y^2-2x(x+1)=1$
$\iff {y’}^2-2x’\left(x’+1\right)=1$
$\iff \left(x’;y’\right)$ définit un TRPI
$\quad$
$(3;5)$ ; $(20;29)$ ; $(119;169)$ ; $(696;985)$ ; $(4~059;5~741)$
Un triangle rectangle sont les côtés de l’angle droit ont pour longueurs $4~059$ et $4~060$ définissent un TRPI dont l’hypoténuse mesure $5~741$.
- Vues: 17718
