Baccalauréat S Asie 18 juin 2013 - Spécialité

Page 9 sur 10: Spécialité

 

Exercice 4 5 points : Spécialité

Candidats ayant choisi l'enseignement de spécialité

Un logiciel permet de transformer un élément rectangulaire d'une photographie.

Ainsi, le rectangle initial OEFG est transformé en un rectangle OE$'$F$'$G$'$, appelé image de OEFG.

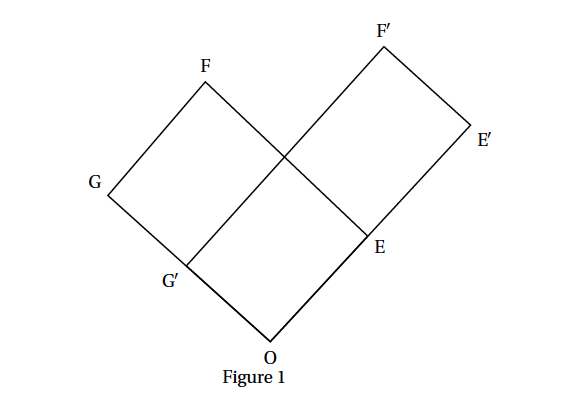
L'objet de cet exercice est d'étudier le rectangle obtenu après plusieurs transformations successives.
Partie A
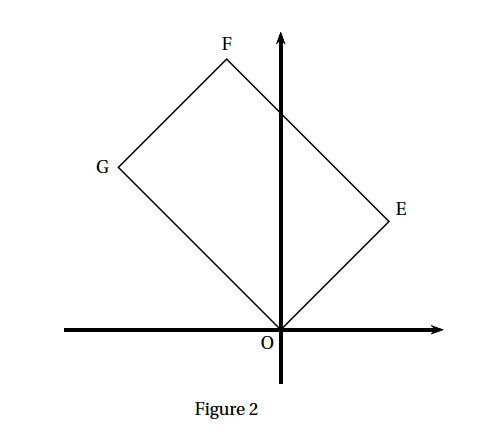
Le plan est rapporté à un repère orthonormé $\left(\text{O},  \vec{i}, \vec{j}\right)$.

Les points E, F et G ont pour coordonnées respectives (2 ; 2), $(-1 ; 5)$ et $(-3 ; 3)$.

La transformation du logiciel associe à tout point $M(x ; y)$ du plan le point $M'(x' ; y')$, image du point $M$ tel que:
\[\left\{\begin{array}{l c l} x'&=&\dfrac{5}{4}x + \dfrac{3}{4}y\\ y'&=&\dfrac{3}{4}x + \dfrac{5}{4}y \end{array}\right.\]

1. 1. Calculer les coordonnées des points E$'$, F$'$ et G$'$, images des points E, F et G par cette transformation.
   2. Comparer les longueurs OE et OE$'$ d'une part, OG et OG$'$ d'autre part. Donner la matrice carrée d'ordre 2, notée $A$, telle que: $\begin{pmatrix}x'\\y' \end{pmatrix}= A \begin{pmatrix}x\\y \end{pmatrix}$.

Partie B
Dans cette partie, on étudie les coordonnées des images successives du sommet F du rectangle OEFG lorsqu'on applique plusieurs fois la transformation du logiciel.

1. On considère l'algorithme suivant destiné à afficher les coordonnées de ces images successives. Une erreur a été commise. Modifier cet algorithme pour qu'il permette d'afficher ces coordonnées.
   $$\begin{array}{|c|l|}\hline \text{Entrée } &\text{ Saisir un entier naturel non nul } N\\ \hline \text{Initialisation }& \text{Affecter à x la valeur } - 1\\ &\text{ Affecter à }y \text{ la valeur 5 }\\ \hline \text{Traitement}&\text{ POUR } i \text{ allant de 1 à } N\\ &\text{Affecter à } a \text{ la valeur } \frac{5}{4} x + \frac{3}{4}y\\ &\text{Affecter à } b \text{ la valeur } \frac{3}{4}x + \frac{5}{4}y\\ &\text{Affecter à } x \text{ la valeur } a\\ &\text{Affecter à } y \text{ la valeur } b\\ &\text{FIN POUR}\\ \hline \text{Sortie} &\text{Afficher } x, \text{ afficher }y\\ \hline \end{array}$$


2. On a obtenu le tableau suivant :
   $$\begin{array}{|c|c|c|c|c|c|c|c|} \hline i &1 &2 &3 &4 &5 &10 &15\\ \hline x &2,5 &7,25 &15,625 &31,8125 &63,9063 &2047,9971 &65535,9999 \\ \hline y &5,5 &8,75 &16,375 &32,1875 &64,0938 &2048,0029 &65536,0001 \\ \hline \end{array}$$ Conjecturer le comportement de la suite des images successives du point F.

Partie C

Dans cette partie, on étudie les coordonnées des images successives du sommet E du rectangle OEFG. On définit la suite des points $E_{n}\left(x_{n} ; y_{n}\right)$ du plan par $E_{0} =$ E et la relation de récurrence :
\[\begin{pmatrix}x_{n+1}\\y_{n+1}\end{pmatrix} = A\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix},\]
où $\left(x_{n+1} ; y_{n+1}\right)$ désignent les coordonnées du point $E_{n+1}$.
Ainsi $x_{0} = 2$ et $y_{0} = 2$.

1. On admet que, pour tout entier $n \geqslant 1$, la matrice $A^n$ peut s'écrire sous la forme : $A^{n} = \begin{pmatrix}\alpha_{n}&\beta_{n}\\\beta_{n}&\alpha_{n}\end{pmatrix}$.
   Démontrer par récurrence que, pour tout entier naturel $n \geqslant 1$, on a : \[\alpha_{n} = 2^{n-1} + \dfrac{1}{2^{n+1}} \quad \text{et}\quad \beta_{n} = 2^{n-1} - \dfrac{1}{2^{n+1}}.\]
2. 1. Démontrer que, pour tout entier naturel $n$, le point $E_{n}$ est situé sur la droite d'équation $y = x$. On pourra utiliser que, pour tout entier naturel $n$, les coordonnées $\left(x_{n} ; y_{n}\right)$ du point $E_{n}$ vérifient :
      \[\begin{pmatrix}x_{n}\\y_{n}\end{pmatrix} = A^n \begin{pmatrix}2\\2\end{pmatrix}.\]
   2. Démontrer que la longueur O$E_{n}$ tend vers $+ \infty$ quand $n$ tend vers $+ \infty$.