Baccalauréat S Asie 18 juin 2013 - Correction de l'Exercice 1

Page 2 sur 10: Correction de l'Exercice 1

Exercice 1 5 points

Commun à tous les candidats

Dans cet exercice, les probabilités seront arrondies au centième.

Partie A
Un grossiste achète des boîtes de thé vert chez deux fournisseurs. Il achète 80 % de ses boîtes chez le fournisseur A et 20 % chez le fournisseur B.
10 % des boîtes provenant du fournisseur A présentent des traces de pesticides et 20 % de celles provenant du fournisseur B présentent aussi des traces de pesticides. On prélève au hasard une boîte du stock du grossiste et on considère les évènements suivants :

• évènement A : «la boîte provient du fournisseur A »
• évènement B : «la boîte provient du fournisseur B »
• évènement S : «la boîte présente des traces de pesticides ».

 

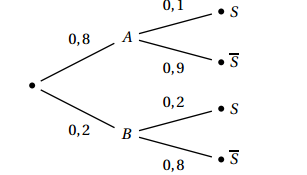
1. Traduire l'énoncé sous forme d'un arbre pondéré.

2. 1. Quelle est la probabilité de l'évènement $B \cap \overline{S}$ ?
   $p \left( B \cap \bar{S} \right) = 0,2 \times 0,8 = 0,16$
   
   2. Justifier que la probabilité que la boîte prélevée ne présente aucune trace de pesticides est égale à $0,88$.
   On utilise la propriété des probabilités totales.
   $p\left( \bar{S} \right) = p \left( A \cap \bar{S} \right) + p \left( B \cap \bar{S} \right)$ $=0,8\times 0,9 + 0,16 $ $=0,88$
3. On constate que la boîte prélevée présente des traces de pesticides.
   Quelle est la probabilité que cette boîte provienne du fournisseur B ?
On cherche $p_S(B) = \dfrac{p(B \cap S)}{p(S)} = \dfrac{0,2 \times 0,2}{1 – 0,88}$ $= \dfrac{1}{3}$ $\approx 0,33$

Partie B
Le gérant d'un salon de thé achète $10$ boîtes chez le grossiste précédent. On suppose que le stock de ce dernier est suffisamment important pour modéliser cette situation par un tirage aléatoire de $10$ boîtes avec remise. On considère la variable aléatoire $X$ qui associe à ce prélèvement de $10$ boîtes, le nombre de boîtes sans trace de pesticides.

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on précisera les paramètres.

On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

• « \3 » considéré comme succès, de probabilité $p=\4$
• « \5 » considéré comme échec, de probabilité $q=1-p=\6$

Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

2. Calculer la probabilité que les 10 boîtes soient sans trace de pesticides.

2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
3. Calculer la probabilité qu'au moins $8$ boîtes ne présentent aucune trace de pesticides.

Partie C
À des fins publicitaires, le grossiste affiche sur ses plaquettes: «88 % de notre thé est garanti sans trace de pesticides ».
Un inspecteur de la brigade de répression des fraudes souhaite étudier la validité de l'affirmation. À cette fin, il prélève $50$ boîtes au hasard dans le stock du grossiste et en trouve $12$ avec des traces de pesticides.
On suppose que, dans le stock du grossiste, la proportion de boîtes sans trace de pesticides est bien égale à $0,88$. On note $F$ la variable aléatoire qui, à tout échantillon de $50$ boîtes, associe la fréquence des boîtes ne contenant aucune trace de pesticides.

1. Donner l'intervalle de fluctuation asymptotique de la variable aléatoire $F$ au seuil de 95 %.

La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$


L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

$$I_{50}= [0,78;0,98]$$
2. L'inspecteur de la brigade de répression peut-il décider, au seuil de 95 %, que la publicité est mensongère ?
La fréquence observée du nombres de boîtes ne contenant pas de pesticides est $f = \frac{50 – 12}{50} = 0,76$.
$~$
Mais $f \notin I_{50}$ et $f < 0,78$. L’échantillon n’est pa représentatif de ce qu’annonce le grossiste.
$~$
L’inspecteur de la brigade de répression peut décider que la publicité est mensongère.