Baccalauréat S Asie 18 juin 2013 - Correction de l'Exercice 2
Exercice 2 6 points
On considère les fonctions $f$ et $g$ définies pour tout réel $x$ par :
\[f(x) = \text{e}^x \quad \text{et}\quad g(x) = 1 - \text{e}^{- x}.\] Les courbes représentatives de ces fonctions dans un repère orthogonal du plan, notées respectivement $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$, sont fournies en annexe.
Partie A
Ces courbes semblent admettre deux tangentes communes. Tracer aux mieux ces tangentes sur la figure de l'annexe. 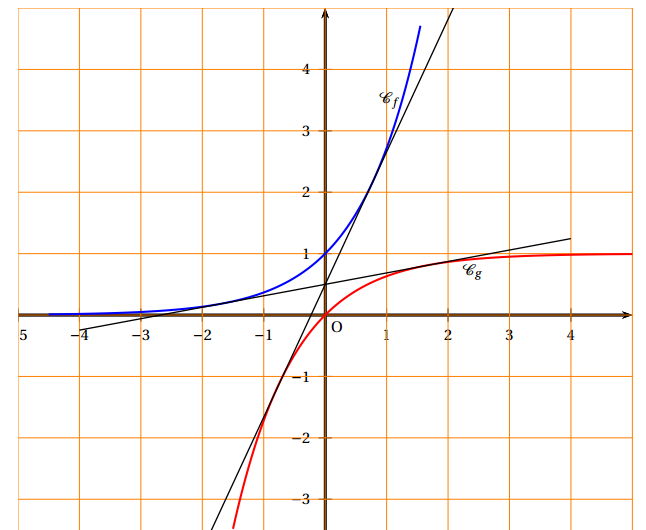
Dans cette partie, on admet l'existence de ces tangentes communes.
On note $\mathcal{D}$ l'une d'entre elles. Cette droite est tangente à la courbe $\mathcal{C}_{f}$ au point A d'abscisse $a$ et tangente à la courbe $\mathcal{C}_{g}$ au point B d'abscisse $b$.
-
- Exprimer en fonction de $a$ le coefficient directeur de la tangente à la courbe $\mathcal{C}_{f}$ au point A. Le coefficient directeur de la tangente à la courbe $\mathcal{C}_{f}$ au point A est égal à $f'(a)$.
- Exprimer en fonction de $b$ le coefficient directeur de la tangente à la courbe $\mathcal{C}_{g}$ au point B. De même le coefficient directeur de la tangente à la courbe $\mathcal{C}_{g}$ au point B est égal à $g'(b)$.
- En déduire que $b = - a$. Si les deux tangentes sont égales le coefficient directeur de leurs équations réduites sont égaux, soit : $f'(a) = g'(b) \iff \text{e}^{a} = \text{e}^{- b}$ et appliquant la fonction logarithme népérien : $a = - b \iff b = - a$.
Or $f'(x) = \text{e}^{x}$,donc $f'(a) = \text{e}^{a}$.
Or $g'(x) = - \left(- \text{e}^{-x}\right)=\text{e}^{-x}$,donc $g'(b) = \text{e}^{- b}$. - Démontrer que le réel $a$ est solution de l'équation \[2( x - 1)\text{e}^x + 1 = 0.\] Une équation réduite de la tangente à la courbe $\mathcal{C}_{f}$ au point A est égale à :
$$y - \text{e}^a = \text{e}^{a}(x - a) \iff y = x\text{e}^{a} + \text{e}^a(1 - a)$$ Une équation réduite de la tangente à la courbe $\mathcal{C}_{g}$ au point B est égale à : $$y - \left(1 - \text{e}^{- b}\right) = \text{e}^{- b}(x - b) \iff y = x\text{e}^{ - b} + 1 - \text{e}^{- b} - b\text{e}^{- b}$$
Ou en remplaçant $- b$ par $a$ : $$y = x\text{e}^{a} + 1 - \text{e}^{a} + a\text{e}^{a} \iff y = x\text{e}^{a} + 1 + \text{e}^{a}(a - 1)$$ Si les deux tangentes sont égales, leurs équations réduites sont les mêmes. On a déjà vu l'égalité des coefficients directeurs.
Les ordonnées à l'origine sont aussi les mêmes soit : $\text{e}^a(1 - a) = 1 + \text{e}^{a}(a - 1) \iff \text{e}^a(2 - 2a) = 1 \iff 2(a - 1)\text{e}^a + 1 = 0$.
Donc $a$ est solution de l'équation dans $\mathbb R$ : $$2( x -1)\text{e}^x + 1 = 0.$$
Partie C
On considère la fonction $\varphi$ définie sur $\mathbb{R}$ par
\[\varphi(x) = 2(x -1)\text{e}^x + 1.\]
-
- Calculer les limites de la fonction $\varphi$ en $- \infty$ et $+ \infty$. Sur $\mathbb R$, : $\varphi(x) = 2x\text{e}^x - 2\text{e}^x + 1$.
- Calculer la dérivée de la fonction $\varphi$, puis étudier son signe. Somme de fonctions dérivable sur $\mathbb R$, $\varphi$ est dérivable sur $\mathbb R$ et : $\varphi'(x) = 2\text{e}^x + 2(x - 1)\text{e}^x = 2x\text{e}^x$.
- Dresser le tableau de variation de la fonction $\varphi$ sur $\mathbb{R}$. Préciser la valeur de $\varphi(0)$. $$\varphi(0)=-2e^0 + 1 = -1$$
On sait que $\displaystyle\lim_{x \to - \infty} \text{e}^x = 0$ et $\displaystyle\lim_{x \to - \infty} x\text{e}^x = 0$, d'où par somme de limite : $\displaystyle\lim_{x to - \infty} \varphi(x) = 1$.
La droite d'équation $y = 1$ est asymptote horizontale à la courbe représentative de $\varphi$.
On a $\displaystyle\lim_{x to + \infty} (x - 1) = + \infty$ et $\displaystyle\lim_{x \to + \infty} \text{e}^x = + \infty$, d'où par somme de limites : $\displaystyle\lim_{x \to + \infty} \varphi(x) = + \infty$.
Comme, quel que soit $x \in \mathbb R$; \: $\text{e}^x > 0$, le signe de $\varphi'(x)$ est celui de $x$. Donc sur $]- \infty~;~0[, \, \varphi'(x) < 0$ : la fonction est décroissante sur cet intervalle et sur $]0~;~+ \infty[$, :$\varphi'(x) > 0$ : la fonction $\varphi$ est croissante sur cet intervalle.
D'où le tableau de variations :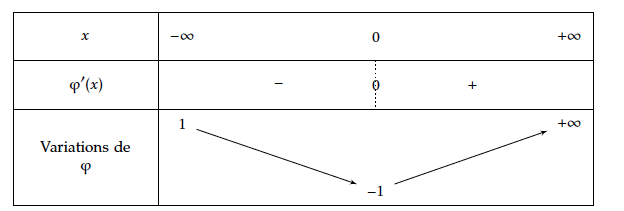
-
- Démontrer que l'équation $\varphi(x) = 0$ admet exactement deux solutions dans $\mathbb{R}$.
- En appliquant le théorème de la bijection sur $]-\infty;0[$ :D'après le théorème de la bijection :$\varphi(-1,68)\approx 0,001$ et $\varphi(-1,67)\approx -0,005$ Ainsi $\varphi(-1,67) <\varphi(\beta)<\varphi(-1,68)$, comme $\varphi$ est strictement décroissante sur $]-\infty;0]$; on déduit : $-1,68\leqslant\beta\leqslant-1,67$
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\1 \left(\3\right)=\5$
$\6\in \left[\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right]$ .$ \beta\approx -1,67$Détaillons la démarche !
La calculatrice donne successivement :
$\varphi(- 2) \approx 0,18$ et $\varphi(- 1) \approx -0,47$, donc $- 2 < \beta < - 1$ ;
$\varphi(- 1,7) \approx 0,013$ et $\varphi(- 1,6) \approx -0,05$, donc $- 1,7 < \beta < - 1,6$ ;
$\varphi(- 1,68) \approx 0,001$ et $\varphi(- 1,67) \approx -0,005$, donc $- 1,68 < \beta < - 1,67$ ;
Conclusion au centième près $\alpha \approx - 1,68$. - En appliquant le théorème de la bijection sur $[0;+\infty[$ :
D'après le théorème de la bijection :
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\1 \left(\3\right)=\5$
$\6\in \left[\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right]$ .
$\varphi(0,76)\approx -0,03$ et $\varphi(0,77)\approx 0,006$\\ Ainsi $\varphi(0,76)<\varphi(\alpha)<\varphi(0,77)$, comme $\varphi$ est strictement croissante sur $[0;+\infty[$; on déduit : $0,76\leqslant\alpha\leqslant0,77$$\alpha\approx 0,77$
- En appliquant le théorème de la bijection sur $]-\infty;0[$ :
- On note $\alpha$ la solution négative de l'équation $\varphi(x) = 0$ et $\beta$ la solution positive de cette équation. À l'aide d'une calculatrice, donner les valeurs de $\alpha$ et $\beta$ arrondies au centième.
- Démontrer que l'équation $\varphi(x) = 0$ admet exactement deux solutions dans $\mathbb{R}$.
Partie D
Dans cette partie, on démontre l'existence de ces tangentes communes, que l'on a admise dans la partie B. On note E le point de la courbe $\mathcal{C}_{f}$ d'abscisse $\alpha$ et F le point de la courbe $\mathcal{C}_{g}$ d'abscisse $- \alpha$ ($\alpha$ est le nombre réel défini dans la partie C).
- Démontrer que la droite (EF) est tangente à la courbe $\mathcal{C}_{f}$ au point E. Démontrons que le coefficient directeur de la droite (EF) est $e^{\alpha}$:
- Démontrer que (EF) est tangente à $\mathcal{C}_{g}$ au point F. Le coefficient directeur de la tangente à la courbe $\mathcal{C}_{g}$ au point d'abscisse $- \alpha$ est $\text{e}^{- (- \alpha)} = \text{e}^{\alpha}.$ On a vu dans la question précédente que la droite (EF) a pour coefficient directeur $\text{e}^{\alpha}$ et contient le point F.
On sait que E appartient à la droite (EF) et à la courbe représentative $\mathcal{C}_{f}$. E$\left(\alpha~;~\text{e}^{\alpha}\right)$ et F$\left(- \alpha~;~1 - \text{e}^{\alpha}\right)$.
Le coefficient directeur de $(EF)$ est $$m_{(EF)}=\dfrac{y_F-y_E}{x_F-x_E}=\dfrac{1-e^{\alpha}-e^{\alpha}}{-\alpha-\alpha}=\dfrac{1-2e^{\alpha}}{-2\alpha}$$ On procède alors par équivalence.
$$\begin{array}{ll} m_{(EF)}=\text{e}^{\alpha}&\iff \dfrac{1-2e^{\alpha}}{-2\alpha}=\text{e}^{\alpha}\\ &\iff 1-2e^{\alpha} =-2\alpha\text{e}^{\alpha}\\ &\iff 2\alpha\text{e}^{\alpha} -2e^{\alpha} +1=0\\ &\iff 2(\alpha-1)\text{e}^{\alpha} +1=0\\ &\iff \varphi(\alpha)=0\end{array}$$ Or l'égalité $ \varphi(\alpha)=0$ est vraie et donc
- Vues: 43870
