Baccalauréat S Nouvelle-Calédonie 19 novembre 2016 - Correction Exercice 4

Page 8 sur 12: Correction Exercice 4

Commun à tous les candidats

On considère le cube ABCDEFGH représenté ci-dessous. On définit les points I et J respectivement par $\vec{\text{HI}} = \dfrac{3}{4} \vec{\text{HG}}$ et $\vec{\text{JG}} = \dfrac{1}{4} \vec{\text{CG}}$.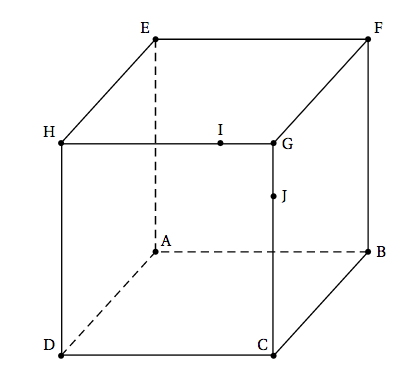

1. Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJK) où K est un point du segment [BF].

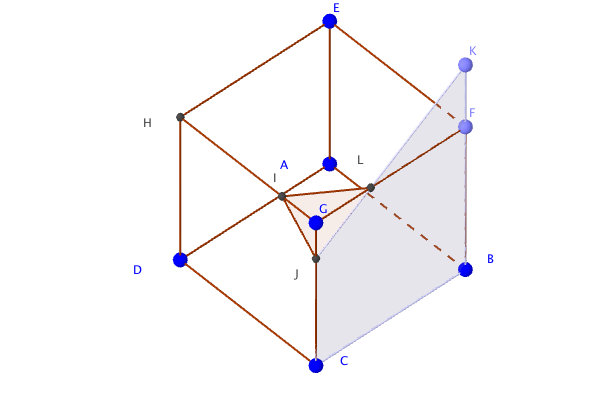
2. Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJL) où L est un point de la droite (BF).

3. Existe-t-il un point P de la droite (BF) tel que la section du cube par le plan (IJP) soit un triangle équilatéral ? Justifier votre réponse.
Dans les triangles $FLP$ et $GPJ$ :
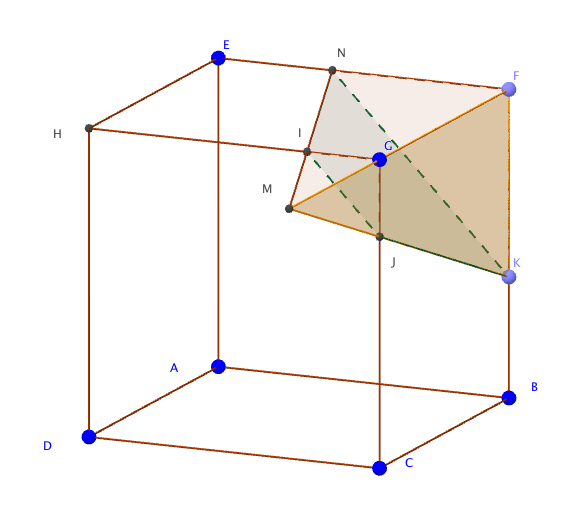
– les droites $(GJ)$ et $(PF)$ sont parallèles;
– les droites $(PJ)$ et $(FG)$ sont sécantes en $N$.
D’après le théorème de Thalès on a :
$\dfrac{NG}{NP}=\dfrac{NJ}{NP}=\dfrac{GJ}{FP}$
Or $\dfrac{GJ}{FP}=\dfrac{1}{3}$
Ainsi $\dfrac{NG}{NP}=\dfrac{1}{3}$ et $GN=GJ$.
Il existe donc un point $P$ de la droite $(BF)$ tel que la section du cube par le plan $(IJP)$ soit un triangle équilatéral.
$\quad$