Baccalauréat S Nouvelle-Calédonie 19 novembre 2016
Exercice 1 4 points
On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~;~ +\infty[$ par \[f(x) = x\text{e}^{- x} - 0,1.\]
- Déterminer la limite de $f$ en $+ \infty$.
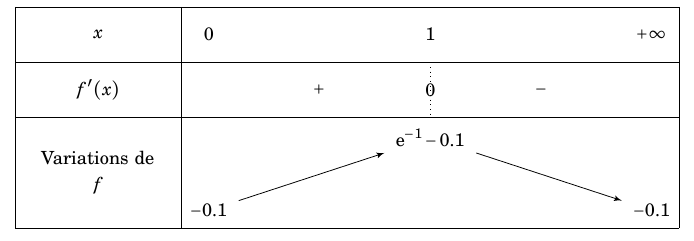
- Étudier les variations de $f$ sur $[0~;~+ \infty[$ et dresser le tableau de variations.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution notée $\alpha$ sur l'intervalle [0 ; 1].
- Démontrer que la fonction $F$, définie sur l'intervalle $[\alpha~;~\beta]$ par \[F(x) = -(x + 1)\text{e}^{- x} - 0,1x\] est une primitive de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$.
- Calculer, en unités d'aire, une valeur arrondie à $0,01$ près de l'aire du domaine compris entre les courbes $\mathcal{C}$ et $\mathcal{C}'$. On utilisera les valeurs arrondies à $0,001$ près suivantes : $\alpha \approx 0,112$ et $\beta \approx 3,577$.
- Sachant que l'on peut disposer 36 plants de tulipes par mètre carré, calculer le nombre de plants de tulipes nécessaire à la réalisation de ce massif.
On admet l'existence du nombre réel strictement positif $\beta$ tel que $\alpha < \beta$ et $f(\beta) = 0$.
On note $\mathcal{C}$ la courbe représentative de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$ dans un repère orthogonal et $\mathcal{C}'$ la courbe symétrique de $\mathcal{C}$ par rapport à l'axe des abscisses.
L'unité sur chaque axe représente 5 mètres.
Ces courbes sont utilisées pour délimiter un massif floral en forme de flamme de bougie sur lequel seront plantées des tulipes. 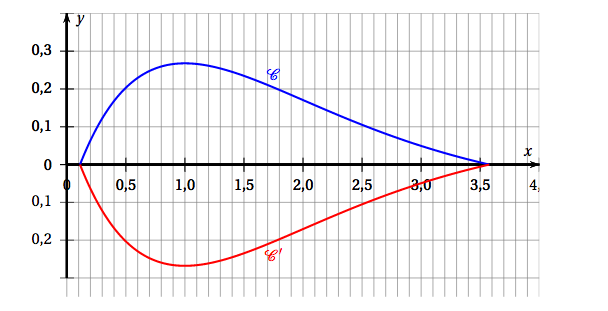
Correction de l'exercice 1 (4 points)
On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~;~ +\infty[$ par \[f(x) = x\text{e}^{- x} - 0,1.\]
- Déterminer la limite de $f$ en $+ \infty$. $f(x)=x\text{e}^{-x}-0,1=\dfrac{x}{\text{e}^x}-0,1=\dfrac{1}{\dfrac{\text{e}^x}{x}}-0,1$.
- Étudier les variations de $f$ sur $[0~;~+ \infty[$ et dresser le tableau de variations. D’après l’énoncé, la fonction $f$ est dérivable sur $[0;+\infty[$.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution notée $\alpha$ sur l'intervalle [0 ; 1].
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = [\2 ; \3]$.
- $\1$ est strictement croissante sur l' intervalle $I = [\2 ; \3]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
- Démontrer que la fonction $F$, définie sur l'intervalle $[\alpha~;~\beta]$ par \[F(x) = -(x + 1)\text{e}^{- x} - 0,1x\] est une primitive de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$. La fonction $F$ est dérivable sur $[\alpha;\beta]$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
- Calculer, en unités d'aire, une valeur arrondie à $0,01$ près de l'aire du domaine compris entre les courbes $\mathcal{C}$ et $\mathcal{C}'$. On utilisera les valeurs arrondies à $0,001$ près suivantes : $\alpha \approx 0,112$ et $\beta \approx 3,577$. Calculons dans un premier temps l’aire du domaine compris entre la courbe l’axe des abscisses, la courbe $\mathscr{C}$ et les droites d’équations $x=\alpha$ et $x=\beta$.
- Sachant que l'on peut disposer 36 plants de tulipes par mètre carré, calculer le nombre de plants de tulipes nécessaire à la réalisation de ce massif. On devra donc planter $36\times 26 = 936$ plants de tulipes.
Or $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} \dfrac{1}{\dfrac{\text{e}^x}{x}}=0$
Par conséquent $ \lim\limits_{x \to +\infty} f(x)=-0,1$.
$\quad$
$f'(x)=\text{e}^{-x}-x\text{e}^{-x}=(1-x)\text{e}^{-x}$
La fonction exponentielle est strictement positive sur $\mathbb R$. Le signe de $f'(x)$ ne dépend donc que de $1-x$.
Ainsi $f$ est croissante sur $[0;1]$ et décroissante sur $[1;+\infty[$.
On obtient donc le tableau de variation suivant :
$\6$ est compris entre $\1\left(\2\right)$ et $\1\left(\3\right)$, en effet $\1\left(\2\right) < \6 $ et $\1\left(\3\right) > \6 $
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $[\2 ; \3]$ .
On admet l'existence du nombre réel strictement positif $\beta$ tel que $\alpha < \beta$ et $f(\beta) = 0$.
On note $\mathcal{C}$ la courbe représentative de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$ dans un repère orthogonal et $\mathcal{C}'$ la courbe symétrique de $\mathcal{C}$ par rapport à l'axe des abscisses.
L'unité sur chaque axe représente 5 mètres.
Ces courbes sont utilisées pour délimiter un massif floral en forme de flamme de bougie sur lequel seront plantées des tulipes. 
$\begin{align*} F'(x)&=-\text{e}^{-x}-\left(-(x+1)\text{e}^{-x}\right)-0,1\\ &=-\text{e}^{-x}+(x+1)\text{e}^{-x}-0,1\\ &=(-1+x+1)\text{e}^{-x}-0,1\\ &=x\text{e}^{-x}-0,1\\ &=f(x)
\end{align*}$
$F$ est bien une primitive de la fonction $f$ sur l’intervalle $[\alpha;\beta]$.
$\quad$
Cette aire vaut :
$\begin{align*} \mathscr{A}_1&=\displaystyle \int_{\alpha}^{\beta}f(x)\text{d}x \\ &=F(\beta)-F(\alpha)
\end{align*}$
Par conséquent, du fait de la symétrie des deux courbes, l’aire du domaine compris entre les courbes $\mathscr{C}$ et $\mathscr{C}’$ vaut :
$\begin{align*} \mathscr{A}&=2\left(F(\beta)-F(\alpha)\right) \\ &=2\left(-(\beta+1)\text{e}^{-\beta}-0,1\beta-\left(-(\alpha+1)\text{e}^{-\alpha}-0,1\alpha\right)\right) \\ &\approx 1,040
\end{align*}$
$\quad$
Le domaine sur chaque axe représente $5$ mètres. L’aire du domaine est donc d’environ $1,040\times 5^2$ soit $26$ m$^2$.
$\quad$
Exercice 2 4 points
La société « Bonne Mamie » utilise une machine pour remplir à la chaîne des pots de confiture. On note $X$ la variable aléatoire qui à chaque pot de confiture produit associe la masse de confiture qu'il contient, exprimée en grammes. Dans le cas où la machine est correctement réglée, on admet que $X$ suit une loi normale de moyenne $\mu = 125$ et d'écart-type $\sigma$.
-
- Pour tout nombre réel $t$ positif, déterminer une relation entre $P(X \leqslant 125 - t)$ et $P(X \geqslant 125 + t)$.
- On sait que 2,3% des pots de confiture contiennent moins de $121$ grammes de confiture. En utilisant la relation précédente, déterminer $P(121 \leqslant X \leqslant 129)$.
- Déterminer une valeur arrondie à l'unité près de $\sigma$ telle que $P(123 \leqslant X \leqslant 127) = 0,68$.
Dans la suite de l'exercice, on suppose que $\sigma = 2$ .
- On estime qu'un pot de confiture est conforme lorsque la masse de confiture qu'il contient est comprise entre $120$ et $130$ grammes.
- On choisit au hasard un pot de confiture de la production. Déterminer la probabilité que ce pot soit conforme. On donnera le résultat arrondi à $10^{-4}$ près.
- On choisit au hasard un pot parmi ceux qui ont une masse de confiture inférieure à $130$~grammes. Quelle est la probabilité que ce pot ne soit pas conforme? On donnera le résultat arrondi à $10^{-4}$ près.
- On admet que la probabilité, arrondie à $10^{-3}$ près, qu'un pot de confiture soit conforme est $0,988$. On choisit au hasard $900$ pots dans la production. On constate que $871$ de ces pots sont conformes. Au seuil de 95 % peut-on rejeter l'hypothèse suivante : « La machine est bien réglée » ?
Correction de l'exercice 2 (4 points)
La société « Bonne Mamie » utilise une machine pour remplir à la chaîne des pots de confiture. On note $X$ la variable aléatoire qui à chaque pot de confiture produit associe la masse de confiture qu'il contient, exprimée en grammes. Dans le cas où la machine est correctement réglée, on admet que $X$ suit une loi normale de moyenne $\mu = 125$ et d'écart-type $\sigma$.
-
- Pour tout nombre réel $t$ positif, déterminer une relation entre $P(X \leqslant 125 - t)$ et $P(X \geqslant 125 + t)$. La variable aléatoire $X$ suit la loi normale de moyenne $\mu=125$.
- On sait que 2,3% des pots de confiture contiennent moins de $121$ grammes de confiture. En utilisant la relation précédente, déterminer $P(121 \leqslant X \leqslant 129)$.
Par conséquent, pour tout nombre réel $t$ positif, on a :
$P(X \leq 125-t)=P(X \geq 125+t)$
$\quad$
Par conséquent $P(X \geq 129)$ $= P(X \geq 125+4)$ $= P(X \leq 125-4)$ $= P(X \leq 121)$ $=0,023$. - Déterminer une valeur arrondie à l'unité près de $\sigma$ telle que $P(123 \leqslant X \leqslant 127) = 0,68$. On sait que $P(\mu-\sigma \leq X \leq \mu+\sigma) \approx 0,68$.
Ainsi $P(121 \leq X \leq 129)$ $=1-\left(P(X \leq 121)+P(X \geq 129)\right)$ $=0,954$.
$\quad$
Or $P(123 \leq X \leq 127)=0,68$
Par conséquent $125-\sigma \approx 123$ et $\sigma \approx 2$.
$\quad$
Remarque : On pouvait faire un raisonnement similaire avec $P(121 \leq X \leq 129) = 0,954$ en utilisant $P(\mu-2\sigma \leq X \leq \mu+2\sigma) \approx 0,954$
$\quad$
Dans la suite de l'exercice, on suppose que $\sigma = 2$ .
- On estime qu'un pot de confiture est conforme lorsque la masse de confiture qu'il contient est comprise entre $120$ et $130$ grammes.
- On choisit au hasard un pot de confiture de la production. Déterminer la probabilité que ce pot soit conforme. On donnera le résultat arrondi à $10^{-4}$ près. On veut calculer $P(120 \leq X \leq 130) \approx 0,987~6$ à $10^{-4}$ près.
- On choisit au hasard un pot parmi ceux qui ont une masse de confiture inférieure à $130$~grammes. Quelle est la probabilité que ce pot ne soit pas conforme? On donnera le résultat arrondi à $10^{-4}$ près. On appelle $C$ l’événement “le pot de confiture est conforme” et $M$ l’événement “le pot de confiture a une masse de confiture inférieure à $130$ grammes”.
$\quad$
On veut calculer :
$\begin{align*} p_M\left(\overline{C}\right)&=\dfrac{p\left(\overline{C}\cap M\right)}{p(M)} \\ &=\dfrac{P(X\leq 120)}{P( X \leq 130)}\\ &=\dfrac{0,5-P(120 \leq X \leq 125)}{0,5+P(125 \leq X \leq 130)} \\ &\approx 0,006~2
\end{align*}$
$\quad$ - On admet que la probabilité, arrondie à $10^{-3}$ près, qu'un pot de confiture soit conforme est $0,988$. On choisit au hasard $900$ pots dans la production. On constate que $871$ de ces pots sont conformes. Au seuil de 95 % peut-on rejeter l'hypothèse suivante : « La machine est bien réglée » ? On note $n=900 \geq 30$, $p=0,988$ donc $np=889,2 \geq 5$ et $n(1-p)=10,8 \geq 5$.
Un intervalle de fluctuation au seuil de $95\%$ de la masse de confiture dans un pot est :
$\begin{align*} I_{900}&=\left[0,988-1,96\sqrt{\dfrac{0,988\times 0,012}{900}};0,988+1,96\sqrt{\dfrac{0,988\times 0,012}{900}}\right] \\ &\approx [0,980;0,996]
\end{align*}$
La fréquence observée est $f=\dfrac{871}{900} \approx 0,968 \notin I_{900}$.
On peut donc rejeter, au risque de $5\%$, l’hypothèse selon laquelle la machine est bien réglée.
$\quad$
Exercice 3 4 points
On se place dans le plan complexe rapporté au repère $\left(\text{O},~\vec{u},~\vec{v}\right)$. Soit $f$ la transformation qui à tout nombre complexe $z$ non nul associe le nombre complexe $f(z)$ défini par : \[f(z) = z + \dfrac{1}{z}.\] On note $M$ le point d'affixe $z$ et $M'$ le point d'affixe $f(z)$.
- On appelle A le point d'affixe $a = - \frac{\sqrt{2}}{2} + \text{i}\frac{\sqrt{2}}{2}$.
- Déterminer la forme exponentielle de $a$.
- Déterminer la forme algébrique de $f(a)$.
- Résoudre, dans l'ensemble des nombres complexes, l'équation $f(z) = 1$.
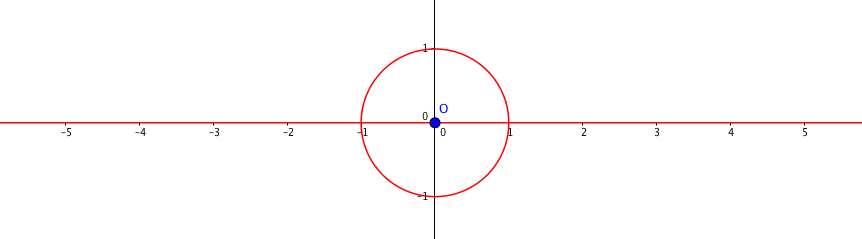
- Soit $M$ un point d'affixe $z$ du cercle $\mathcal C$ de centre O et de rayon 1.
- Justifier que l'affixe $z$ peut s'écrire sous la forme $z = \text{e}^{\text{i}\theta}$ avec $\theta$ un nombre réel.
- Montrer que $f(z)$ est un nombre réel.
- Décrire et représenter l'ensemble des points $M$ d'affixe $z$ tels que $f(z)$ soit un nombre réel.
Correction de l'exercice 3 (4 points)
On se place dans le plan complexe rapporté au repère $\left(\text{O},~\vec{u},~\vec{v}\right)$. Soit $f$ la transformation qui à tout nombre complexe $z$ non nul associe le nombre complexe $f(z)$ défini par : \[f(z) = z + \dfrac{1}{z}.\] On note $M$ le point d'affixe $z$ et $M'$ le point d'affixe $f(z)$.
- On appelle A le point d'affixe $a = - \frac{\sqrt{2}}{2} + \text{i}\frac{\sqrt{2}}{2}$.
- Déterminer la forme exponentielle de $a$. $|a|=\sqrt{\dfrac{1}{2}+\dfrac{1}{2}}=1$
- Déterminer la forme algébrique de $f(a)$. $\begin{align*} f(a)&=\text{e}^{3\text{i} \pi/4} + \dfrac{1}{\text{e}^{3\text{i} \pi/4}} \\ &=\text{e}^{3\text{i} \pi/4} + \text{e}^{-3\text{i} \pi/4} \\ &=-\dfrac{\sqrt{2}}{2}+\text{i} \dfrac{\sqrt{2}}{2} -\dfrac{\sqrt{2}}{2}-\text{i} \dfrac{\sqrt{2}}{2} \\ &=-\sqrt{2}
Donc $a=\text{e}^{3\text{i} \pi/4}$.
$\quad$
\end{align*}$
$\quad$ - Résoudre, dans l'ensemble des nombres complexes, l'équation $f(z) = 1$. $\quad$
- Soit $M$ un point d'affixe $z$ du cercle $\mathcal C$ de centre O et de rayon 1.
- Justifier que l'affixe $z$ peut s'écrire sous la forme $z = \text{e}^{\text{i}\theta}$ avec $\theta$ un nombre réel. Tout nombre complexe $z$ peut s’écrire sous la forme $z=|z|\text{e}^{\text{i} \theta}$.
- Montrer que $f(z)$ est un nombre réel.
Or ici $|z|=OM=1$.
Donc $z$ peut s’écrire sous la forme $z=\text{e}^{\text{i} \theta}$.
$\begin{align*} f(z)&=\text{e}^{\text{i} \theta}+\dfrac{1}{\text{e}^{\text{i} \theta}} \\ &=\text{e}^{\text{i} \theta}+\text{e}^{-\text{i} \theta} \\ &=\cos(\theta)+\text{i} \sin(\theta)+\cos(-\theta)+\text{i} \sin(-\theta) \\ &=\cos(\theta)+\text{i} \sin(\theta)+\cos(\theta)-\text{i} \sin(\theta) \\ &=2\cos(\theta)
\end{align*}$
Donc $f(z)$ est un nombre réel.
Remarque : On a en fait redémontré la formule d’Euler pour le cosinus.
$\quad$ - Décrire et représenter l'ensemble des points $M$ d'affixe $z$ tels que $f(z)$ soit un nombre réel. On note $z=r\text{e}^{\text{i} \theta}$ avec $r>0$
$\begin{align*} f(z)=1 &\iff z+\dfrac{1}{z}=1 \\ &\iff z^2+1=z \quad \text{et } z\neq 0 \\ &\iff z^2-z+1=0 \quad \text{et} z\neq 0
\end{align*}$
$\Delta=(-1)^2-4\times 1\times 1 = -3<0$.
Il y a donc deux racines complexes conjuguées :
$z_1=\dfrac{1-\text{i}\sqrt{3}}{2}$ et $z_2=\dfrac{1+\text{i}\sqrt{3}}{2}$
$\quad$
$\begin{align*} f(z)&=r\text{e}^{\text{i} \theta}+\dfrac{1}{r\text{e}^{\text{i} \theta}} \\ &=r\text{e}^{\text{i} \theta}+\dfrac{1}{r}\text{e}^{-\text{i} \theta} \\ &=r\cos(\theta)+r\text{i} \sin(\theta)+\dfrac{1}{r}\cos(\theta)-\dfrac{\text{i}}{r}\sin(\theta) \\ &=r\cos(\theta)+\dfrac{1}{r}\cos(\theta)+\text{i}\left(r\sin(\theta)-\dfrac{1}{r}\sin(\theta)\right)
\end{align*}$
$f(z)$ est un nombre réel si, et seulement si, $r\sin(\theta)-\dfrac{1}{r}\sin(\theta)=0$.
Or $r\sin(\theta)-\dfrac{1}{r}\sin(\theta)=\sin(\theta)\left(r-\dfrac{1}{r}\right)$.
Ainsi $f(z)$ est un réel si, et seulement si, $\sin(\theta)=0$ ou $r-\dfrac{1}{r}=0$.
Or $\sin(\theta)=0 \iff \theta = k\pi$ où $k\in \mathbb Z$ : $z$ est un réel non nul.
Et $r-\dfrac{1}{r}=0 \iff r=1$ ou $r=-1$ : $r=-1$ est impossible.
Donc l’ensemble des points $M$ d’affixe $z$ tels que $f(z)$ soit un nombre réel est composé du cercle trigonométrique et de l’axe des réels privé de l’origine du repère.
Exercice 4 3 points
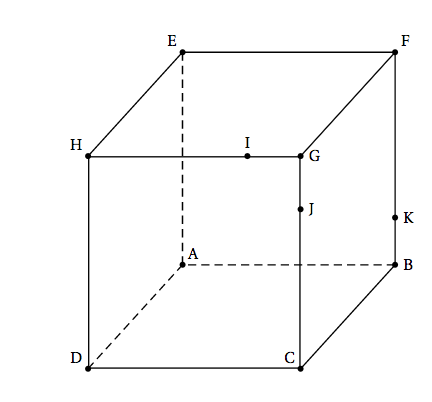
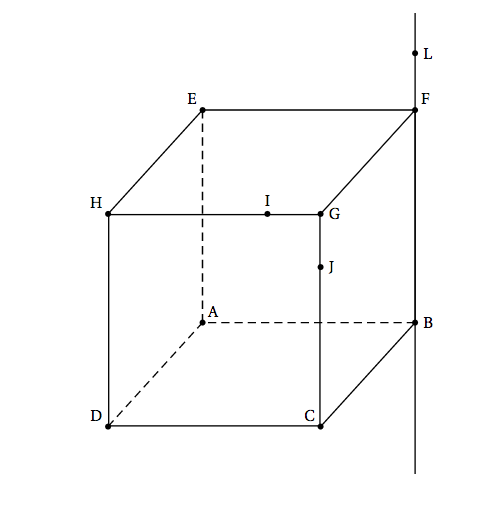
On considère le cube ABCDEFGH représenté ci-dessous. On définit les points I et J respectivement par $\vec{\text{HI}} = \dfrac{3}{4} \vec{\text{HG}}$ et $\vec{\text{JG}} = \dfrac{1}{4} \vec{\text{CG}}$. 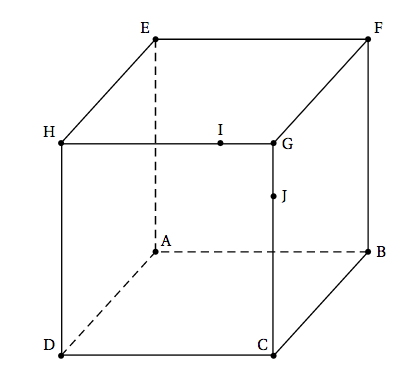
- Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJK) où K est un point du segment [BF].
- Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJL) où L est un point de la droite (BF).
- Existe-t-il un point P de la droite (BF) tel que la section du cube par le plan (IJP) soit un triangle équilatéral ? Justifier votre réponse.
Annexe de l'exercice 4
On considère le cube ABCDEFGH représenté ci-dessous. On définit les points I et J respectivement par $\vec{\text{HI}} = \dfrac{3}{4} \vec{\text{HG}}$ et $\vec{\text{JG}} = \dfrac{1}{4} \vec{\text{CG}}$. 
- Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJK) où K est un point du segment [BF].
- Sur le document réponse donné en annexe, à rendre avec la copie , tracer, sans justifier, la section du cube par le plan (IJL) où L est un point de la droite (BF).
- Existe-t-il un point P de la droite (BF) tel que la section du cube par le plan (IJP) soit un triangle équilatéral ? Justifier votre réponse. Dans les triangles $FLP$ et $GPJ$ :
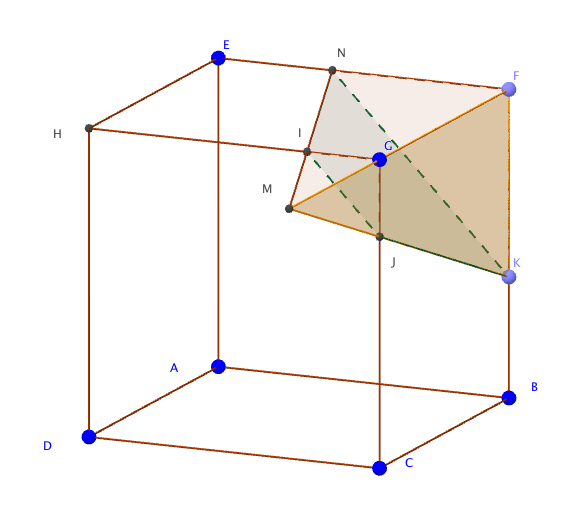
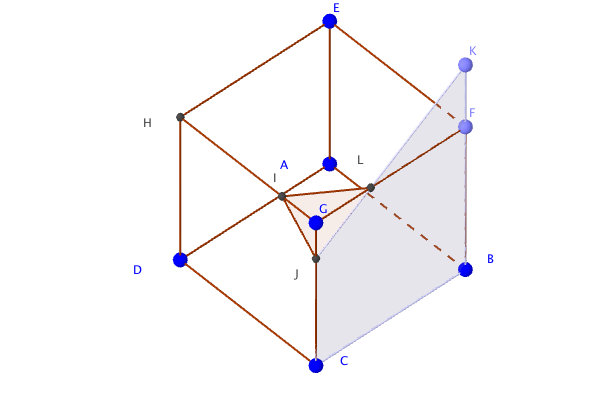
– les droites $(GJ)$ et $(PF)$ sont parallèles;
– les droites $(PJ)$ et $(FG)$ sont sécantes en $N$.
D’après le théorème de Thalès on a :
$\dfrac{NG}{NP}=\dfrac{NJ}{NP}=\dfrac{GJ}{FP}$
Or $\dfrac{GJ}{FP}=\dfrac{1}{3}$
Ainsi $\dfrac{NG}{NP}=\dfrac{1}{3}$ et $GN=GJ$.
Il existe donc un point $P$ de la droite $(BF)$ tel que la section du cube par le plan $(IJP)$ soit un triangle équilatéral.
$\quad$
Exercice 5 5 points
Un apiculteur étudie l'évolution de sa population d'abeilles. Au début de son étude, il évalue à 10000 le nombre de ses abeilles. Chaque année, l'apiculteur observe qu'il perd 20 % des abeilles de l'année précédente. Il achète un nombre identique de nouvelles abeilles chaque année. On notera $c$ ce nombre exprimé en dizaines de milliers. On note $u_0$ le nombre d'abeilles, en dizaines de milliers, de cet apiculteur au début de l'étude. Pour tout entier naturel $n$ non nul, $u_n$ désigne le nombre d'abeilles, en dizaines de milliers, au bout de la $n$-ième année. Ainsi, on a \[u_0 = 1\quad \text{et, pour tout entier naturel }\:n,\: u_{n+ 1} = 0,8u_n + c.\]
Partie A
On suppose dans cette partie seulement que $c = 1$.
- Conjecturer la monotonie et la limite de la suite $\left(u_n\right)$.
- Démontrer par récurrence que, pour tout entier naturel $n,\: u_n = 5 - 4 \times 0,8^n$.
- Vérifier les deux conjectures établies à la question 1. en justifiant votre réponse. Interpréter ces deux résultats.
Partie B
L'apiculteur souhaite que le nombre d'abeilles tende vers 100000 . On cherche à déterminer la valeur de $c$ qui permet d'atteindre cet objectif. On définit la suite $\left(v_n\right)$ par, pour tout entier naturel $n,\: v_n = u_n - 5c$.
- Montrer que la suite $\left(v_n\right)$ est une suite géométrique dont on précisera la raison et le premier terme.
- En déduire une expression du terme général de la suite $\left(v_n\right)$en fonction de $n$.
- Déterminer la valeur de $c$ pour que l'apiculteur atteigne son objectif.
CORRECTION DE l' Exercice 5 5 points
Un apiculteur étudie l'évolution de sa population d'abeilles. Au début de son étude, il évalue à 10000 le nombre de ses abeilles. Chaque année, l'apiculteur observe qu'il perd 20 % des abeilles de l'année précédente. Il achète un nombre identique de nouvelles abeilles chaque année. On notera $c$ ce nombre exprimé en dizaines de milliers. On note $u_0$ le nombre d'abeilles, en dizaines de milliers, de cet apiculteur au début de l'étude. Pour tout entier naturel $n$ non nul, $u_n$ désigne le nombre d'abeilles, en dizaines de milliers, au bout de la $n$-ième année. Ainsi, on a \[u_0 = 1\quad \text{et, pour tout entier naturel }\:n,\: u_{n+ 1} = 0,8u_n + c.\]
Partie A
On suppose dans cette partie seulement que $c = 1$.
- Conjecturer la monotonie et la limite de la suite $\left(u_n\right)$. A l’aide de la calculatrice on obtient :
- Démontrer par récurrence que, pour tout entier naturel $n,\: u_n = 5 - 4 \times 0,8^n$. Initialisation : Si $n=0$ $u_0=1$ et $5-4\times 0,8^n=5-4=1$.
- Vérifier les deux conjectures établies à la question 1. en justifiant votre réponse. Interpréter ces deux résultats. Pour tout entier naturel $n$ on a :
$u_0=1 \quad u_1=1,8 \quad u_2=2,44 \quad u_3=2,952 \quad u_4=3,361~6$
Il semblerait donc que la suite $\left(u_n\right)$ soit croissante.
Sa limite semble être $5$.
$\quad$
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $u_n=5-4\times 0,8^n$.
$\begin{align*} u_{n+1}&=0,8u_n+1 \\ &=0,8\left(5-4\times 0,8^n\right)+1\\ &=4-4\times 0,8^{n+1}+1\\ &=5-4\times 0,8^{n+1}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Pour tout entier naturel$n$ on a donc $u_n=5-4\times 0,8^n$.
$\quad$
$\begin{align*} u_{n+1}-u_n&=5-4\times 0,8^{n+1}-\left(5-4\times 0,8^n\right) \\ &=-4\times 0,8^{n+1}+4\times 0,8^n \\ &=4\times 0,8^n(-0,8+1) \\ &=4\times 0,8^n\times 0,2 \\ &=0,8^{n+1} \\ &>0
\end{align*}$
La suite $\left(u_n\right)$ est donc croissante.
$\quad$
Puisque $-1<0,8<1$ alors $\lim\limits_{n \to +\infty}0,8^n=0$
Par conséquent $\lim\limits_{n \to +\infty} u_n=5$.
$\quad$
Si l’apiculteur achète chaque année $10~000$ abeilles alors son nombres d’abeilles augmentera chaque année et sera de $50~000$ au bout d’un grand nombre d’années.
$\quad$
Partie B
L'apiculteur souhaite que le nombre d'abeilles tende vers 100000 . On cherche à déterminer la valeur de $c$ qui permet d'atteindre cet objectif. On définit la suite $\left(v_n\right)$ par, pour tout entier naturel $n,\: v_n = u_n - 5c$.
- Montrer que la suite $\left(v_n\right)$ est une suite géométrique dont on précisera la raison et le premier terme. Pour tout entier naturel $n$ on a :
- En déduire une expression du terme général de la suite $\left(v_n\right)$en fonction de $n$. Ainsi, pour tout entier naturel $n$ on a : $v_n=(1-5c)\times 0,8^n$
- Déterminer la valeur de $c$ pour que l'apiculteur atteigne son objectif. On a alors, pour tout entier naturel $n$ : $u_n=(1-5c)\times 0,8^n+5c$
$\begin{align*} v_{n+1}&=u_{n+1}-5c \\ &=0,8u_n+c-5c\\ &=0,8u_n-4c\\ &=0,8\left(u_n-5c\right) \\ &=0,8v_n
\end{align*}$
$\quad$
autre méthode : $u_n=v_n+5c$.
$\begin{align*} v_{n+1}&=u_{n+1}-5c \\ &=0,8u_n+c-5c\\ &=0,8u_n-4c\\ &=0,8\left(v_n+5c\right)-4c\\ &=0,8v_n+4c-4c\\ &=0,8v_n
\end{align*}$
La suite $\left(v_n\right)$ est donc géométrique de raison $0,8$ et de premier terme $v_0=u_0-5c=1-5c$.
$\quad$
$\quad$
Pour la même raison qu’à la question A.3 $\lim\limits_{n \to +\infty} u_n=5c$.
L’apiculteur souhaite que $\lim\limits_{n \to +\infty} u_n=10$.
Il faut donc que $c=2$.
Spécialité 5 points
On observe la taille d'une colonie de fourmis tous les jours. Pour tout entier naturel $n$ non nul, on note $u_n$ le nombre de fourmis, exprimé en milliers. dans cette population au bout du $n$-ième jour. Au début de l'étude la colonie compte 5000 fourmis et au bout d'un jour elle compte 5100 fourmis. Ainsi, on a $u_0 = 5$ et $u_1 = 5,1$. On suppose que l'accroissement de la taille de la colonie d'un jour sur l'autre diminue de 10 % chaque jour. En d'autres termes. pour tout entier naturel $n$, \[u_{n+2} - u_{n+1} = 0,9\left(u_{n+1} - u_n\right).\]
- Démontrer, dans ces conditions, que $u_2 = 5,19$.
- Pour tout entier naturel $n$, on pose $V_n = \begin{pmatrix}u_{n+1}\\u_n\end{pmatrix}$ et $A = \begin{pmatrix}1,9& -0,9\\1& 0\end{pmatrix}$.
- Démontrer que, pour tout entier naturel $n$, on a $V_{n+1} = AV_n$. On admet alors que, pour tout entier naturel $n,\: V_n = A^nV_0$.
- On pose $P = \begin{pmatrix}0,9&1\\1&1\end{pmatrix}$. On admet que la matrice $P$ est inversible. À l'aide de la calculatrice, déterminer la matrice $P^{-1}$. En détaillant les calculs, déterminer la matrice $D$ définie par $D = P^{-1} AP$.
- Démontrer par récurrence que, pour tout entier naturel $n$, on a $A^n = PD^nP^{-1}$. Pour tout entier naturel $n$, on admet que \[A^n = \begin{pmatrix}-10 \times 0,9^{n+1} + 10& 10 \times 0,9^{n+1} - 9\\ - 10 \times 0,9^n + 10& 10 \times 0,9^n - 9\end{pmatrix}.\]
- En déduire que, pour tout entier naturel $n$ : $u_n = 6 - 0,9^n$.
- Calculer la taille de la colonie au bout du 10e jour. On arrondira le résultat à une fourmi près.
- Calculer la limite de la suite $\left(u_n\right)$. Interpréter ce résultat dans le contexte.
Correction de l'exercice de Spécialité 5 points
On observe la taille d'une colonie de fourmis tous les jours. Pour tout entier naturel $n$ non nul, on note $u_n$ le nombre de fourmis, exprimé en milliers. dans cette population au bout du $n$-ième jour. Au début de l'étude la colonie compte 5000 fourmis et au bout d'un jour elle compte 5100 fourmis. Ainsi, on a $u_0 = 5$ et $u_1 = 5,1$. On suppose que l'accroissement de la taille de la colonie d'un jour sur l'autre diminue de 10 % chaque jour. En d'autres termes. pour tout entier naturel $n$, \[u_{n+2} - u_{n+1} = 0,9\left(u_{n+1} - u_n\right).\]
- Démontrer, dans ces conditions, que $u_2 = 5,19$. $u_{n+2}-u_{n+1}=0,9\left(u_{n+1}-u_n\right)$
- Pour tout entier naturel $n$, on pose $V_n = \begin{pmatrix}u_{n+1}\\u_n\end{pmatrix}$ et $A = \begin{pmatrix}1,9& -0,9\\1& 0\end{pmatrix}$.
- Démontrer que, pour tout entier naturel $n$, on a $V_{n+1} = AV_n$. On admet alors que, pour tout entier naturel $n,\: V_n = A^nV_0$. $\begin{align*}AV_n&=\begin{pmatrix}1,9&-0,9\\1&0\end{pmatrix} \begin{pmatrix}u_{n+1}\\u_n\end{pmatrix} \\ &=\begin{pmatrix}1,9u_{n+1}-0,9u_n\\u_{n+1}\end{pmatrix} \\ &=\begin{pmatrix}u_{n+2}\\u_{n+1}\end{pmatrix}\\ &=V_{n+1}
- On pose $P = \begin{pmatrix}0,9&1\\1&1\end{pmatrix}$. On admet que la matrice $P$ est inversible. À l'aide de la calculatrice, déterminer la matrice $P^{-1}$. En détaillant les calculs, déterminer la matrice $D$ définie par $D = P^{-1} AP$. A l’aide de la calculatrice on obtient $P^{-1}=\begin{pmatrix}-10&10\\10&-9\end{pmatrix}$
- Démontrer par récurrence que, pour tout entier naturel $n$, on a $A^n = PD^nP^{-1}$. Pour tout entier naturel $n$, on admet que \[A^n = \begin{pmatrix}-10 \times 0,9^{n+1} + 10& 10 \times 0,9^{n+1} - 9\\ - 10 \times 0,9^n + 10& 10 \times 0,9^n - 9\end{pmatrix}.\] Initialisation : Si $n=0$ alors $PD^0P^{-1} = PP^{-1}=I_2$ où $I_2$ est la matrice identité d’ordre $2$.
- En déduire que, pour tout entier naturel $n$ : $u_n = 6 - 0,9^n$. On sait que $V_n=A^nV_0$
\end{align*}$
$\quad$
$\begin{align*}D&=P^{-1}AP \\ &=\begin{pmatrix}-10&10\\10&-9\end{pmatrix} \times \begin{pmatrix}1,9&-0,9\\1&0\end{pmatrix} \times \begin{pmatrix}0,9&1\\1&1\end{pmatrix} \\ &=\begin{pmatrix}-19+10&9\\19-9&-9\end{pmatrix}\times \begin{pmatrix}0,9&1\\1&1\end{pmatrix} \\ &=\begin{pmatrix}-9&10\\10&-9\end{pmatrix} \times\begin{pmatrix}0,9&1\\1&1\end{pmatrix} \\ &=\begin{pmatrix}-8,1+9&-10+10\\9-9&10-9\end{pmatrix} \\ &=\begin{pmatrix}0,9&0\\0&1\end{pmatrix}
\end{align*}$
$\quad$
$A^0=I_2$.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $A^n=PD^nP^{-1}$.
On sait que $D=P^{-1}AP$ donc $PDP^{-1}=A$.
$\begin{align*} A^{n+1}&=A^n \times A \\ &=PD^nP^{-1} \times PDP^{-1} \\ &=PD^nDP^{-1} \\ &=PD^{n+1}P^{-1}
\end{align*}$
La propriété est donc vraie au rang $n+1$
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $A^n=PD^nP^{-1}$.
$\quad$
Donc $\begin{pmatrix}u_{n+1}\\u_n\end{pmatrix} = \begin{pmatrix} 5,1\left(-10\times 0,9^{n+1}+10\right)+5\left(10\times 0,9^{n+1}-9\right) \\5,1\left(-10\times 0,9^n+10\right)+5\left(10\times 0,9^n-9\right)\end{pmatrix}$
Par conséquent
$\begin{align*} u_n&=5,1\left(-10\times 0,9^n+10\right)+5\left(10\times 0,9^n-9\right) \\ &=-51\times 0,9^n+51+50\times 0,9^n-45 \\ &=6-0,9^n
\end{align*}$
$\quad$ - Calculer la taille de la colonie au bout du 10e jour. On arrondira le résultat à une fourmi près. $u_{10}=6-0,9^{10}\approx 5,651$.
- Calculer la limite de la suite $\left(u_n\right)$. Interpréter ce résultat dans le contexte. $-1 <0,9<1$ donc $\lim\limits_{n \to +\infty}0,9^n=0$.
Donc $u_{n+2}=u_{n+1}+0,9\left(u_{n+1}-u_n\right)=1,9u_{n+1}-0,9u_n$
Ainsi
$\begin{align*} u_2&=1,9u_1-0,9u_0 \\ &=1,9\times 5,1-0,9\times 5\\ &=5,19
\end{align*}$
La colonie compte donc environ $5~651$ fourmis au bout du $10^{\e}$ jour.
$\quad$
Par conséquent $\lim\limits_{n \to +\infty} u_n=6$.
Au bout d’un grand nombre de jours, la colonie comptera $6~000$ fourmis.
- Vues: 48933
