Baccalauréat S Nouvelle-Calédonie 19 novembre 2016 - Correction Exercice 3
Page 6 sur 12
Correction de l'exercice 3 (4 points)
On se place dans le plan complexe rapporté au repère $\left(\text{O},~\vec{u},~\vec{v}\right)$. Soit $f$ la transformation qui à tout nombre complexe $z$ non nul associe le nombre complexe $f(z)$ défini par : \[f(z) = z + \dfrac{1}{z}.\] On note $M$ le point d'affixe $z$ et $M'$ le point d'affixe $f(z)$.
- On appelle A le point d'affixe $a = - \frac{\sqrt{2}}{2} + \text{i}\frac{\sqrt{2}}{2}$.
- Déterminer la forme exponentielle de $a$. $|a|=\sqrt{\dfrac{1}{2}+\dfrac{1}{2}}=1$
- Déterminer la forme algébrique de $f(a)$. $\begin{align*} f(a)&=\text{e}^{3\text{i} \pi/4} + \dfrac{1}{\text{e}^{3\text{i} \pi/4}} \\ &=\text{e}^{3\text{i} \pi/4} + \text{e}^{-3\text{i} \pi/4} \\ &=-\dfrac{\sqrt{2}}{2}+\text{i} \dfrac{\sqrt{2}}{2} -\dfrac{\sqrt{2}}{2}-\text{i} \dfrac{\sqrt{2}}{2} \\ &=-\sqrt{2}
Donc $a=\text{e}^{3\text{i} \pi/4}$.
$\quad$
\end{align*}$
$\quad$ - Résoudre, dans l'ensemble des nombres complexes, l'équation $f(z) = 1$. $\quad$
- Soit $M$ un point d'affixe $z$ du cercle $\mathcal C$ de centre O et de rayon 1.
- Justifier que l'affixe $z$ peut s'écrire sous la forme $z = \text{e}^{\text{i}\theta}$ avec $\theta$ un nombre réel. Tout nombre complexe $z$ peut s’écrire sous la forme $z=|z|\text{e}^{\text{i} \theta}$.
- Montrer que $f(z)$ est un nombre réel.
Or ici $|z|=OM=1$.
Donc $z$ peut s’écrire sous la forme $z=\text{e}^{\text{i} \theta}$.
$\begin{align*} f(z)&=\text{e}^{\text{i} \theta}+\dfrac{1}{\text{e}^{\text{i} \theta}} \\ &=\text{e}^{\text{i} \theta}+\text{e}^{-\text{i} \theta} \\ &=\cos(\theta)+\text{i} \sin(\theta)+\cos(-\theta)+\text{i} \sin(-\theta) \\ &=\cos(\theta)+\text{i} \sin(\theta)+\cos(\theta)-\text{i} \sin(\theta) \\ &=2\cos(\theta)
\end{align*}$
Donc $f(z)$ est un nombre réel.
Remarque : On a en fait redémontré la formule d’Euler pour le cosinus.
$\quad$ - Décrire et représenter l'ensemble des points $M$ d'affixe $z$ tels que $f(z)$ soit un nombre réel. On note $z=r\text{e}^{\text{i} \theta}$ avec $r>0$
$\begin{align*} f(z)=1 &\iff z+\dfrac{1}{z}=1 \\ &\iff z^2+1=z \quad \text{et } z\neq 0 \\ &\iff z^2-z+1=0 \quad \text{et} z\neq 0
\end{align*}$
$\Delta=(-1)^2-4\times 1\times 1 = -3<0$.
Il y a donc deux racines complexes conjuguées :
$z_1=\dfrac{1-\text{i}\sqrt{3}}{2}$ et $z_2=\dfrac{1+\text{i}\sqrt{3}}{2}$
$\quad$
$\begin{align*} f(z)&=r\text{e}^{\text{i} \theta}+\dfrac{1}{r\text{e}^{\text{i} \theta}} \\ &=r\text{e}^{\text{i} \theta}+\dfrac{1}{r}\text{e}^{-\text{i} \theta} \\ &=r\cos(\theta)+r\text{i} \sin(\theta)+\dfrac{1}{r}\cos(\theta)-\dfrac{\text{i}}{r}\sin(\theta) \\ &=r\cos(\theta)+\dfrac{1}{r}\cos(\theta)+\text{i}\left(r\sin(\theta)-\dfrac{1}{r}\sin(\theta)\right)
\end{align*}$
$f(z)$ est un nombre réel si, et seulement si, $r\sin(\theta)-\dfrac{1}{r}\sin(\theta)=0$.
Or $r\sin(\theta)-\dfrac{1}{r}\sin(\theta)=\sin(\theta)\left(r-\dfrac{1}{r}\right)$.
Ainsi $f(z)$ est un réel si, et seulement si, $\sin(\theta)=0$ ou $r-\dfrac{1}{r}=0$.
Or $\sin(\theta)=0 \iff \theta = k\pi$ où $k\in \mathbb Z$ : $z$ est un réel non nul.
Et $r-\dfrac{1}{r}=0 \iff r=1$ ou $r=-1$ : $r=-1$ est impossible.
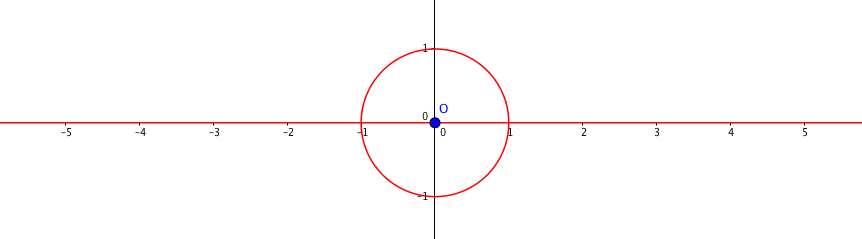
Donc l’ensemble des points $M$ d’affixe $z$ tels que $f(z)$ soit un nombre réel est composé du cercle trigonométrique et de l’axe des réels privé de l’origine du repère.
- Vues: 49021
