Baccalauréat S Nouvelle-Calédonie 19 novembre 2016
Page 1 sur 12
Exercice 1 4 points
On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~;~ +\infty[$ par \[f(x) = x\text{e}^{- x} - 0,1.\]
- Déterminer la limite de $f$ en $+ \infty$.
- Étudier les variations de $f$ sur $[0~;~+ \infty[$ et dresser le tableau de variations.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution notée $\alpha$ sur l'intervalle [0 ; 1].
- Démontrer que la fonction $F$, définie sur l'intervalle $[\alpha~;~\beta]$ par \[F(x) = -(x + 1)\text{e}^{- x} - 0,1x\] est une primitive de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$.
- Calculer, en unités d'aire, une valeur arrondie à $0,01$ près de l'aire du domaine compris entre les courbes $\mathcal{C}$ et $\mathcal{C}'$. On utilisera les valeurs arrondies à $0,001$ près suivantes : $\alpha \approx 0,112$ et $\beta \approx 3,577$.
- Sachant que l'on peut disposer 36 plants de tulipes par mètre carré, calculer le nombre de plants de tulipes nécessaire à la réalisation de ce massif.
On admet l'existence du nombre réel strictement positif $\beta$ tel que $\alpha < \beta$ et $f(\beta) = 0$.
On note $\mathcal{C}$ la courbe représentative de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$ dans un repère orthogonal et $\mathcal{C}'$ la courbe symétrique de $\mathcal{C}$ par rapport à l'axe des abscisses.
L'unité sur chaque axe représente 5 mètres.
Ces courbes sont utilisées pour délimiter un massif floral en forme de flamme de bougie sur lequel seront plantées des tulipes. 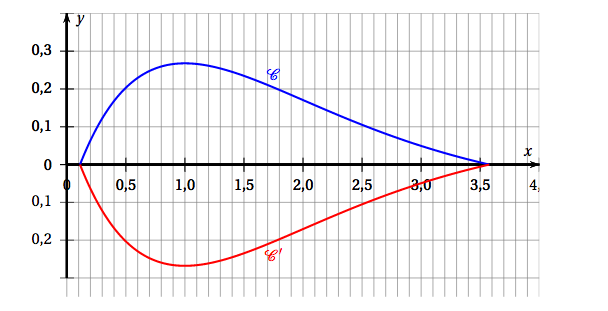
- Vues: 48690
