Baccalauréat S Métropole 19 juin 2014 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

1. On désigne par $\mathcal{P}$ le plan qui passe par A et qui est orthogonal à la droite (DF).
On note H le point d'intersection du plan $\mathcal{P}$ et de la droite (DF).
1. Donner les coordonnées des points D et F.
Dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AC}}, \vec{\text{AD}}\right)$ on a D $(0\,, 0\,,1)$ et F milieu de B $(1\,, 0\,,0)$ C $(0\,, 1\,,0)$ donc F a pour coordonnées $(\dfrac{1+0}{2}\,,\dfrac{0+1}{2}\,,0)=(\dfrac{1}{2}\,,\dfrac{1}{2}\,,0)$

2. Donner une représentation para métrique de la droite (DF).
Ainsi $ \vec{\text{DF}} $ a pour coordonnées $\left (\dfrac{1}{2}-0\,,\dfrac{1}{2}-0\,,1-0\right )$ $M(x~;~y~;~z) \in (DF)$ vérifie $\overrightarrow{DM}=t \overrightarrow{DF}$, on a donc: $ \left\lbrace \begin{array}{l l} x-0 &= \dfrac{1}{2}t\\ y-0 &= \dfrac{1}{2}t\\ z-1 &= t \end{array} \right. \iff \left\lbrace \begin{array}{l l} x&= \dfrac{1}{2}t\\ y&= \dfrac{1}{2}t\\ z&= 1-t \end{array} \right.$
3. Déterminer une équation cartésienne du plan $\mathcal{P}$.
$\mathcal{P}$ a pour vecteur normal $ \vec{\text{DF}} $ car $\mathcal{P}$ est orthogonal à la droite (DF).
Ainsi $\mathcal{P}$ a une équation cartésienne du type $$ \dfrac{1}{2}x+ \dfrac{1}{2}y-z+d=0$$ $A (0\,,0\,,0\,,0)\in \mathcal{P}$ donc $d=0$.
$\mathcal{P}$ admet pour équation cartésienne $\dfrac{1}{2}x+\dfrac{1}{2}y-z=0$ $\mathcal{P}$ admet pour équation cartésienne $x+y-2z=0$
4. Calculer les coordonnées du point H.
$H(x~;~y~;~z) \in (DF \cap \mathcal{P})$ vérifie le système : $ \left\lbrace \begin{array}{l l} x+y-2z&=0 \; (1)\\ x &= \dfrac{1}{2}t\\ y &= \dfrac{1}{2}t\\ z &= 1-t \end{array} \right.$ $(1)\iff \dfrac{1}{2}t +\dfrac{1}{2}t-2(1-t)=0 \iff 3t =2 \iff t=\dfrac{2}{3}$
En reportant $t=\dfrac{2}{3}$ dans la représentation paramétrique de la droite (DF) on obtient : H a pour coordonnées $\left(\dfrac{1}{3}\,,\dfrac{1}{3}\,,\dfrac{1}{3}\right)$
5. Démontrer que l'angle $\widehat{\text{EHG}}$ est un angle droit.
On a $\overrightarrow{EH}\begin{pmatrix}\dfrac{1}{3}-\dfrac{1}{2}\\\dfrac{1}{3}\\\dfrac{1}{3}\end{pmatrix} =\begin{pmatrix}-\dfrac{1}{6}\\\dfrac{1}{3}\\\dfrac{1}{3}\end{pmatrix}$ et $\overrightarrow{EH}\begin{pmatrix}\dfrac{1}{3}\\\dfrac{1}{3}-\dfrac{1}{2}\\\dfrac{1}{3}\end{pmatrix} =\begin{pmatrix}\dfrac{1}{3}\\-\dfrac{1}{6}\\\dfrac{1}{3}\end{pmatrix}$ $$ \overrightarrow{EH}\cdot\overrightarrow{GH}=-\dfrac{1}{6}\times \dfrac{1}{3}+\left(-\dfrac{1}{6}\times \dfrac{1}{3}\right)+\dfrac{1}{3}\times\dfrac{1}{3}=-\dfrac{1}{18}-\dfrac{1}{18}+\dfrac{1}{9}=0$$ Ainsi $\overrightarrow{EH}\cdot \overrightarrow{GH}=0$, ce qui prouve que l'angle $\widehat{\text{EHG}}$ est un angle droit.
2. On désigne par $M$ un point de la droite (DF) et par $t$ le réel tel que $\vec{\text{D}M} = t\vec{\text{DF}}$. On note $\alpha$ la mesure en radians de l'angle géométrique $\widehat{\text{E}M\text{G}}$. Le but de cette question est de déterminer la position du point $M$ pour que $\alpha$ soit maximale.
   1. Démontrer que $M\text{E}^2 = \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}$.
   $M$ un point de la droite (DF) et par $t$ le réel tel que $\vec{\text{D}M} = t\vec{\text{DF}}$ a pour coordonnées $(x\,,y\,,z)$ tels que : $ \left\lbrace \begin{array}{l l} x &= \dfrac{1}{2}t\\ y &= \dfrac{1}{2}t\\ z &= 1-t \end{array} \right.$
   $$\overrightarrow{ME}\begin{pmatrix}\dfrac{1}{2}-\dfrac{1}{2}t\\0-\dfrac{1}{2}t\\t-1\end{pmatrix} =\begin{pmatrix} \dfrac{1}{2}(1-t)\\ -\dfrac{1}{2}t\\t-1\end{pmatrix}$$ $$\text{ Ainsi : }$$ $$\begin{array}{l l} ME^2&=\left( \dfrac{1}{2}(1-t)\right)^2+\left(-\dfrac{1}{2}t\right)^2+\left(t-1\right)^2 \\ &= \dfrac{1}{4}(t-1)^2+\dfrac{1}{4}t^2+(t-1)^2\\ &= \dfrac{5}{4}(t-1)^2+\dfrac{1}{4}t^2\\ &= \dfrac{5}{4}(t^2-2t+1)+\dfrac{1}{4}t^2\\ &= \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}\\ \end{array}$$
   2. Démontrer que le triangle $M$EG est isocèle en $M$. En déduire que $M\text{E}\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{1}{2\sqrt{2}}$.
   On a G milieu de A $(0\,, 0\,,0)$ C $(0\,, 1\,,0)$ donc G a pour coordonnées $(0\,,\dfrac{1}{2}\,,0)$ $$\overrightarrow{MG}\begin{pmatrix}\dfrac{1}{2}t\\ \dfrac{1}{2}t -\dfrac{1}{2}\\1-t\end{pmatrix} =\begin{pmatrix} \dfrac{1}{2}(1-t)\\ -\dfrac{1}{2}t\\t-1\end{pmatrix}$$ $$\text{ Ainsi : }$$ $$\begin{array}{l l} MG^2&=\left(\dfrac{1}{2}t\right)^2+\left( \dfrac{1}{2}(t-1)\right)^2+\left(1-t\right)^2 \\ &= \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}\\ &= ME^2\\ \end{array}$$ Ayant $MG^2=ME^2$; on a prouvé que $ME=MG$ et donc le triangle $M$EG est isocèle en $M$.
   3. Justifier que $\alpha$ est maximale si et seulement si $\sin \left(\dfrac{\alpha}{2} \right)$ est maximal. En déduire que $\alpha$ est maximale si et seulement si $M\text{E}^2$ est minimal.
   On appelle $K$ le milieu de $[EG]$. La droite $(MK)$ est donc une hauteur et une bissectrice du triangle $MEG$ et $\widehat{EMK} = \dfrac{\alpha}{2}$.
   Dans le triangle $MEG$ rectangle en $K$ on a : $\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME}$
   Or $EK = \dfrac{EG}{2} = \dfrac{\sqrt{0,5}}{2} = \dfrac{1}{2\sqrt{2}}$.
   Par conséquent :
   $$ \sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME} \Leftrightarrow ME \sin \left(\dfrac{\alpha}{2} \right) = \dfrac{1}{2\sqrt{2}}$$.
   $~$
   Première méthode : La fonction $\sin$ est strictement croissante sur $\left[0;\dfrac{\pi}{2}\right]$.
   Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal.
   $~$
   Deuxième méthode : Les fonctions $\alpha \mapsto \alpha $ et $\alpha \sin\left( \dfrac{\alpha}{2} \right)$ sont dérivables sur $\mathbb{R}$.
   $ \left(\sin\left( \dfrac{\alpha}{2} \right) \right)’ = \dfrac{\alpha’}{2} \cos \left( \dfrac{\alpha}{2} \right) $.
   $\alpha$ ne prend des valeurs que dans $[0;\pi]$ donc $\cos \left( \dfrac{\alpha}{2} \right) \geq 0$ Par conséquent :
   le signe de $\left(sin\left( \dfrac{\alpha}{2} \right) \right)’ $ = le signe de $\alpha’$.
   Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal.
   $~$
   $~$
   $~$
   Le produit $ME \sin \left(\dfrac{\alpha}{2} \right) $ est constant.
   Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal $\Leftrightarrow ME$ minimal.
   $~$
   
   4. Conclure.
      • Première méthode : Pour déterminer le minimum de $ME$ on va trouver la valeur de $t$ telle que $\dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}$ soit minimal.
        Il s’agit de trouver l’abscisse du sommet de la parabole correspondante :
        $$x_S = \dfrac{-b}{2a} = \dfrac{5}{6}$$
        Par conséquent les coordonnées du point $M$ cherché sont $\left( \dfrac{5}{12};\dfrac{5}{12};\dfrac{1}{6} \right)$.
      • Deuxième méthode : on étudie les variation de $\phi : t \mapsto : \dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}$
        $\phi$ est dérivable sur $\mathbb{R}$ et $$\phi '(t)=\dfrac{3}{2}\times 2t -\dfrac{5}{2} =3t - \dfrac{5}{2}$$ $$\phi '(t) >0 \iff 3t - \dfrac{5}{2} >0 \iff t>\dfrac{5}{6} $$
        d' où le tableau de variation de $\phi$ sur $\mathbb{R}$ :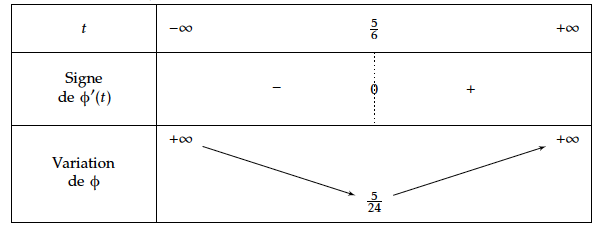
        
        $$\phi \left (\frac{5}{24}\right) =\frac{3}{2}\times \frac{25}{36} -\frac{5}{2}\times \frac{5}{6} +\frac{5}{4}=\frac{5}{24}$$ Par conséquent les coordonnées du point $M$ cherché sont $\left( \dfrac{5}{12};\dfrac{5}{12};\dfrac{1}{6} \right)$.
        On a alors $\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME} =\dfrac{\frac{1}{2\sqrt 2}}{\sqrt{\frac{5}{24}}}=\sqrt{\dfrac{3}{5}}$
        On déduit $\dfrac{\alpha}{2}=\sin ^{-1} \left (\sqrt{\dfrac{3}{5}}\right ) $
        Le maximum de l'angle $\alpha$ est donc $2\sin ^{-1} \left (\sqrt{\dfrac{3}{5}}\right )\approx 101,5 ^{\circ}$
      Une figure dynamique avec Geogebra 3D :