Baccalauréat S Métropole 19 juin 2014 - Correction Exercice 1
Correction de l'exercice 1 (5 points)
PartieA
- Justifier que $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
- Déterminer le tableau de variation de la fonction $f_1$. Onprécisera les limites de $f_1$ en $+\infty$ et en $-\infty$ .
- Limite en $+\infty$ : $\left.\begin{array}{l} \lim\limits_{x \to +\infty}~\text{e}^{-x}=0\\ \lim\limits_{x \to +\infty}~x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to+\infty} f_1(x)=+\infty$
- Limite en $-\infty$ : on factorise par le terme prépondérant $$f_1(x) = x + e^{-x}=e^{-x}\left (1+xe^x\right )$$ On utilise la limite de référence : $\lim\limits_{x \to -\infty}~x\text{e}^{x}=0$
$\left.\begin{array}{l} \lim\limits_{x \to -\infty}~\left (1+xe^x\right )=1\\ \lim\limits_{x \to -\infty}~e^{-x}=+\infty \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to-\infty} f_1(x) =+\infty$ - $f_1$ est dérivable comme somme de fonctions dérivables et $f_1'(x)=1-\text{e}^{-x}$
On a utilisé la formule de dérivation : $$\left (e^u\right )'=u'e^u$$ Signe de la dérivée : $$f'_1(x)>0 \Leftrightarrow 1-\text{e}^{-x}> 0 \Leftrightarrow -\text{e}^{-x}>-1\Leftrightarrow \text{e}^{-x} < 1 \Leftrightarrow - x < \ln 1 \Leftrightarrow - x < 0 \Leftrightarrow x > 0$$ $$f_1 '(x)=0 \Leftrightarrow x = 0.$$
- Le tableau de variation de $f_1$ :
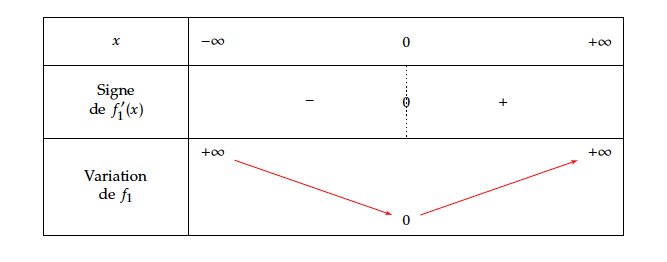
A $\in \mathcal{C}_1\iff f_1(0)=1$, or $f_1(0)=0+e^0=1$
Ayant $f_1(0)=1$, $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
L 'objet de cette partie est d'étudier la suite $\left (I_n\right )$ définie sur $\mathbb{R}$ par : $I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$
- Dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, pour tout entier naturel $n$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ définie sur $\mathbb{R}$ par : $$f_n(x)=x+e^{-nx}$$
Sur le graphique ci-dessous on a tracé la courbe $\mathcal{C}_n$ pour plusieurs valeurs de l'entier $n$ et la droite $\mathcal{D}$ d'équation $x=1$.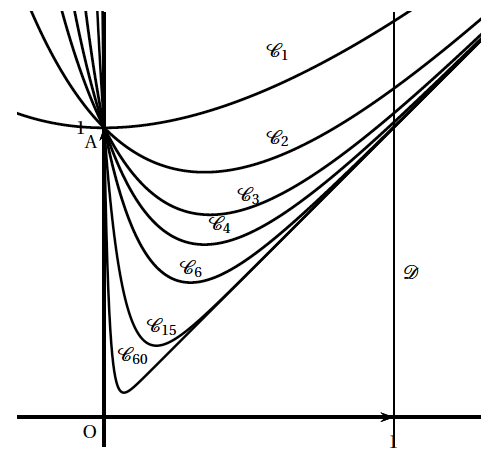
- Interpréter géométriquement l'intégrale $I_n$.
- En utilisant cette interprétation, formuler une conjecture sur le sens de variation de la suite $\left (I_n\right )$ et sa limite éventuelle. On précisera les éléments sur lesquels on s'appuie pour conjecturer. La suite $\left (I_n\right )$ semble décroissante et minorée par 0, et semble converger vers $\dfrac{1}{2}$, l'aire du triangle OIB où I(1;0) et B(1;1).
La fonction $f_n$ est clairement continue et positive sur l'intervalle $[0;1]$, en effet si $x\in [0;1]$ alors $x\geq 0 $ et pour tout réel $x$ , on a $e^{-nx}>0$, d'où par somme $f_n(x)>0$.
$I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$ représente donc l'aire délimitée par $\mathcal{C}_n$, l'axe des abscisses et les droites d'équation $x=0$ et $x=1$.
$$ \begin{array}{ l l l } I_{n+1} -I_n & =\displaystyle\int_0^1\left (x+e^{-(n+1)x}\right )\;\text{d}x-\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x & \\ &= \displaystyle\int_0^1\left (x+e^{-(n+1)x}\right )-\left (x+e^{-nx}\right ) \;\text{d}x & \text{Linéarité de l'intégrale}\\ &= \displaystyle\int_0^1\left ( e^{-(n+1)x}-e^{-nx}\right ) \;\text{d}x & \\ &= \displaystyle\int_0^1 e^{-(n+1)x}\left (1-e^{x}\right ) \;\text{d}x &e^{-(n+1)x}\times e^{x} = e^{-(n+1)x+x}=e^{-nx} \\ \end{array}$$ $$I_{n+1} -I_n =\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x$$ Pour tout réel $x \in [0;1]$ on a :
$0 \leq x \leq1$, la fonction exponentielle étant strictement croissante sur $\mathbb{R}$, on déduit :
$e^0 \leq e^x \leq e^1$, soit $1\leq e^x $ ce qui donne $1- e^x \leq 0$ $\left.\begin{array}{l} 1- e^x \leq 0 \\ e^{-(n+1)x} >0 \end{array}\right\}$ par produit on obtient: $e^{-(n+1)x} \left( 1-e^{x}\right ) \leq 0 $
En intégrant cette dernière inégalité de 0 à 1 ; 0 < 1 on obtient $\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x \leq 0 $
Ainsi $I_{n+1} -I_n\leq 0 $
- Ayant pour tout entier $n$; $I_{n+1} -I_n\leq 0 $, la suite $\left (I_n\right )$ est décroissante
- Par ailleurs comme $f_n$ est positive sur [0;1], par positivité de l'intégrale, on déduit $I_n \geq 0$, et donc la suite $\left (I_n\right )$ est minorée par 0.
- On conclut que la suite $\left (I_n\right )$ est convergente car elle est décroissante et minorée.
Tout d'abord
$$\begin{array}{ l l }I_0&=\displaystyle\int_0^1\left (x+e^{- 0\times x}\right )\;\text{d}x\\ &=\displaystyle\int_0^1\left (x+1\right )\;\text{d}x \\ &=\left [\dfrac{x^2}{2}+x\right ]_0^1\\ &=\dfrac{1}{2}+1-0=\dfrac{3}{2}\end{array}$$
$$I_0=\dfrac{3}{2}$$ Par ailleurs si $n\geq 1$, on a :
$$\begin{array} { l l } I_n &=\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x \\ &=\left [\dfrac{x^2}{2}-\dfrac{e^{-nx}}{n}\right ]_0^1 \\ &=\left [\dfrac{x^2}{2}-\dfrac{e^{-nx}}{n}\right ]_0^1 \text{ ici } n\neq 0\\ &= \dfrac{1}{2}-\dfrac{e^{-n}}{n}-\left (0 -\dfrac{e^{0}}{n}\right)\\ &= \dfrac{1}{2}-\dfrac{e^{-n}}{n}+\dfrac{1}{n} \\ \end{array}$$ $\left.\begin{array}{l} \lim\limits_{n \to +\infty}~ e^{-n}=0\\ \lim\limits_{n \to +\infty}~\dfrac{1}{n} =0 \end{array}\right\}$ par produit on obtient: $\lim\limits_{n \to +\infty} -\dfrac{e^{-n}}{n} =0$
$\left.\begin{array}{l} \lim\limits_{n \to +\infty}~ \dfrac{1}{2} +\dfrac{1}{n}=\dfrac{1}{2}\\ \lim\limits_{n \to +\infty}~-\dfrac{e^{-n}}{n} =0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{n \to +\infty} I_n =\dfrac{1}{2}$
- Vues: 23041
