Baccalauréat S Métropole 19 juin 2014
Exercice 1 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par $\mathcal{C}_1$ la courbe représentative de la fonction $f_1$ définie sur $\mathbb{R}$ par : $$f_1(x)=x+e^{-x}$$
- Justifier que $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
- Déterminer le tableau de variation de la fonction $f_1$. Onprécisera les limites de $f_1$ en $+\infty$ et en $-\infty$ .
Partie B
L 'objet de cette partie est d'étudier la suite $\left (I_n\right )$ définie sur $\mathbb{R}$ par : $I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$
- Dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, pour tout entier naturel $n$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ définie sur $\mathbb{R}$ par : $$f_n(x)=x+e^{-nx}$$
Sur le graphique ci-dessous on a tracé la courbe $\mathcal{C}_n$ pour plusieurs valeurs de l'entier $n$ et la droite $\mathcal{D}$ d'équation $x=1$.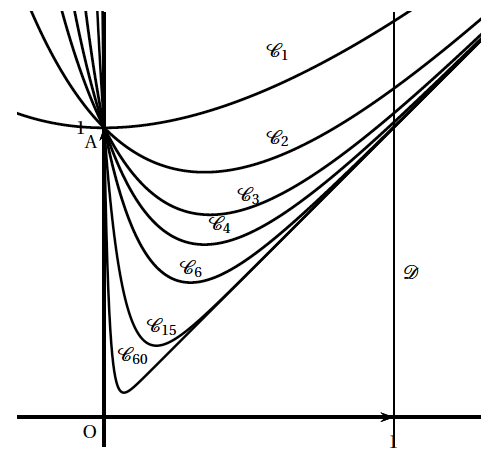
- Interpréter géométriquement l'intégrale $I_n$.
- En utilisant cette interprétation, formuler une conjecture sur le sens de variation de la suite $\left (I_n\right )$ et sa limite éventuelle. On précisera les éléments sur lesquels on s'appuie pour conjecturer.
- Démontrer que pour tout entier naturel $n$ supérieur ou égal à 1, $$I_{n+1} -I_n =\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x$$ En déduire le signe de $I_{n+1} -I_n $ puis démontrer que la suite $\left (I_n\right )$ est convergente.
- Déterminer l'expression de $I_n$ en fonction de $n$ et déterminer la limite de la suite $\left (I_n\right )$.
Correction de l'exercice 1 (5 points)
PartieA
- Justifier que $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
- Déterminer le tableau de variation de la fonction $f_1$. Onprécisera les limites de $f_1$ en $+\infty$ et en $-\infty$ .
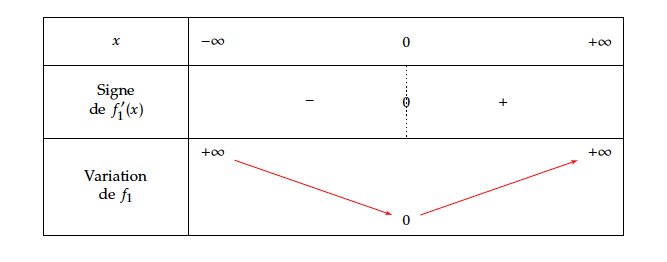
- Limite en $+\infty$ : $\left.\begin{array}{l} \lim\limits_{x \to +\infty}~\text{e}^{-x}=0\\ \lim\limits_{x \to +\infty}~x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to+\infty} f_1(x)=+\infty$
- Limite en $-\infty$ : on factorise par le terme prépondérant $$f_1(x) = x + e^{-x}=e^{-x}\left (1+xe^x\right )$$ On utilise la limite de référence : $\lim\limits_{x \to -\infty}~x\text{e}^{x}=0$
$\left.\begin{array}{l} \lim\limits_{x \to -\infty}~\left (1+xe^x\right )=1\\ \lim\limits_{x \to -\infty}~e^{-x}=+\infty \end{array}\right\}$ par produit on obtient: $\lim\limits_{x \to-\infty} f_1(x) =+\infty$ - $f_1$ est dérivable comme somme de fonctions dérivables et $f_1'(x)=1-\text{e}^{-x}$
On a utilisé la formule de dérivation : $$\left (e^u\right )'=u'e^u$$ Signe de la dérivée : $$f'_1(x)>0 \Leftrightarrow 1-\text{e}^{-x}> 0 \Leftrightarrow -\text{e}^{-x}>-1\Leftrightarrow \text{e}^{-x} < 1 \Leftrightarrow - x < \ln 1 \Leftrightarrow - x < 0 \Leftrightarrow x > 0$$ $$f_1 '(x)=0 \Leftrightarrow x = 0.$$
- Le tableau de variation de $f_1$ :
A $\in \mathcal{C}_1\iff f_1(0)=1$, or $f_1(0)=0+e^0=1$
Ayant $f_1(0)=1$, $\mathcal{C}_1$ passe par le point A de coordonnées (0,1).
L 'objet de cette partie est d'étudier la suite $\left (I_n\right )$ définie sur $\mathbb{R}$ par : $I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$
- Dans le plan muni d'un repère orthonormé $\left(\text{O},~\vec{i},\vec{j}\right)$, pour tout entier naturel $n$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ définie sur $\mathbb{R}$ par : $$f_n(x)=x+e^{-nx}$$
Sur le graphique ci-dessous on a tracé la courbe $\mathcal{C}_n$ pour plusieurs valeurs de l'entier $n$ et la droite $\mathcal{D}$ d'équation $x=1$.
- Interpréter géométriquement l'intégrale $I_n$.
- En utilisant cette interprétation, formuler une conjecture sur le sens de variation de la suite $\left (I_n\right )$ et sa limite éventuelle. On précisera les éléments sur lesquels on s'appuie pour conjecturer. La suite $\left (I_n\right )$ semble décroissante et minorée par 0, et semble converger vers $\dfrac{1}{2}$, l'aire du triangle OIB où I(1;0) et B(1;1).
La fonction $f_n$ est clairement continue et positive sur l'intervalle $[0;1]$, en effet si $x\in [0;1]$ alors $x\geq 0 $ et pour tout réel $x$ , on a $e^{-nx}>0$, d'où par somme $f_n(x)>0$.
$I_n =\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x$ représente donc l'aire délimitée par $\mathcal{C}_n$, l'axe des abscisses et les droites d'équation $x=0$ et $x=1$.
$$ \begin{array}{ l l l } I_{n+1} -I_n & =\displaystyle\int_0^1\left (x+e^{-(n+1)x}\right )\;\text{d}x-\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x & \\ &= \displaystyle\int_0^1\left (x+e^{-(n+1)x}\right )-\left (x+e^{-nx}\right ) \;\text{d}x & \text{Linéarité de l'intégrale}\\ &= \displaystyle\int_0^1\left ( e^{-(n+1)x}-e^{-nx}\right ) \;\text{d}x & \\ &= \displaystyle\int_0^1 e^{-(n+1)x}\left (1-e^{x}\right ) \;\text{d}x &e^{-(n+1)x}\times e^{x} = e^{-(n+1)x+x}=e^{-nx} \\ \end{array}$$ $$I_{n+1} -I_n =\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x$$ Pour tout réel $x \in [0;1]$ on a :
$0 \leq x \leq1$, la fonction exponentielle étant strictement croissante sur $\mathbb{R}$, on déduit :
$e^0 \leq e^x \leq e^1$, soit $1\leq e^x $ ce qui donne $1- e^x \leq 0$ $\left.\begin{array}{l} 1- e^x \leq 0 \\ e^{-(n+1)x} >0 \end{array}\right\}$ par produit on obtient: $e^{-(n+1)x} \left( 1-e^{x}\right ) \leq 0 $
En intégrant cette dernière inégalité de 0 à 1 ; 0 < 1 on obtient $\displaystyle\int_0^1 e^{-(n+1)x} \left( 1-e^{x}\right )\;\text{d}x \leq 0 $
Ainsi $I_{n+1} -I_n\leq 0 $
- Ayant pour tout entier $n$; $I_{n+1} -I_n\leq 0 $, la suite $\left (I_n\right )$ est décroissante
- Par ailleurs comme $f_n$ est positive sur [0;1], par positivité de l'intégrale, on déduit $I_n \geq 0$, et donc la suite $\left (I_n\right )$ est minorée par 0.
- On conclut que la suite $\left (I_n\right )$ est convergente car elle est décroissante et minorée.
Tout d'abord
$$\begin{array}{ l l }I_0&=\displaystyle\int_0^1\left (x+e^{- 0\times x}\right )\;\text{d}x\\ &=\displaystyle\int_0^1\left (x+1\right )\;\text{d}x \\ &=\left [\dfrac{x^2}{2}+x\right ]_0^1\\ &=\dfrac{1}{2}+1-0=\dfrac{3}{2}\end{array}$$
$$I_0=\dfrac{3}{2}$$ Par ailleurs si $n\geq 1$, on a :
$$\begin{array} { l l } I_n &=\displaystyle\int_0^1\left (x+e^{-nx}\right )\;\text{d}x \\ &=\left [\dfrac{x^2}{2}-\dfrac{e^{-nx}}{n}\right ]_0^1 \\ &=\left [\dfrac{x^2}{2}-\dfrac{e^{-nx}}{n}\right ]_0^1 \text{ ici } n\neq 0\\ &= \dfrac{1}{2}-\dfrac{e^{-n}}{n}-\left (0 -\dfrac{e^{0}}{n}\right)\\ &= \dfrac{1}{2}-\dfrac{e^{-n}}{n}+\dfrac{1}{n} \\ \end{array}$$ $\left.\begin{array}{l} \lim\limits_{n \to +\infty}~ e^{-n}=0\\ \lim\limits_{n \to +\infty}~\dfrac{1}{n} =0 \end{array}\right\}$ par produit on obtient: $\lim\limits_{n \to +\infty} -\dfrac{e^{-n}}{n} =0$
$\left.\begin{array}{l} \lim\limits_{n \to +\infty}~ \dfrac{1}{2} +\dfrac{1}{n}=\dfrac{1}{2}\\ \lim\limits_{n \to +\infty}~-\dfrac{e^{-n}}{n} =0 \end{array}\right\}$ par somme on obtient: $\lim\limits_{n \to +\infty} I_n =\dfrac{1}{2}$
Exercice 2 5 points
Les parties A et B peuvent être traitées indépendamment.
Partie A
Un laboratoire pharmaceutique propose des tests de dépistage de diverses maladies. Son service de communication met en avant les caractéristiques suivantes :
- la probabilité qu'une personne malade présente un test positif est $0,99$ ;
- la probabilité qu'une personne saine présente un test positif est $0,001$.
- Pour une maladie qui vient d'apparaître, le laboratoire élabore un nouveau test. Une étude statistique permet d'estimer que le pourcentage de personnes malades parmi la population d'une métropole est égal à 0,1 %.
On choisit au hasard une personne dans cette population et on lui fait subir le test.
On note $M$ l'évènement « la personne choisie est malade» et $T$ l'évènement « le test est positif » .- Traduire l'énoncé sous la forme d'un arbre pondéré.
- Démontrer que la probabilité $p(T)$ de l'évènement $T$ est égale à $1,989 \times 10^{-3}$.
- L'affirmation suivante est-elle vraie ou fausse ? Justifier la réponse. Affirmation : « Si le test est positif, il y a moins d'une chance sur deux que la personne soit malade » .
- Le laboratoire décide de commercialiser un test dès lors que la probabilité qu'une personne testée positivement soit malade est supérieure ou égale à $0,95$.
On désigne par $x$ la proportion de personnes atteintes d'une certaine maladie dans la population. À partir de quelle valeur de $x$ le laboratoire commercialise-t-il le test correspondant ?
Partie B
La chaine de production du laboratoire fabrique, en très grande quantité, le comprimé d'un médicament.
- Un comprimé est conforme si sa masse est comprise entre 890 et 920 mg.
On admet que la masse en milligrammes d'un comprimé pris au hasard dans la production peut être modélisée par une variable aléatoire $X$ qui suit la loi normale $\mathcal{N}\left(\mu,~\sigma^2\right)$, de moyenne $\mu = 900$ et d'écart-type $\sigma = 7$.- Calculer la probabilité qu'un comprimé prélevé au hasard soit conforme. On arrondira à $10^{-2}$.
- Déterminer l'entier positif $h$ tel que $P(900 - h \leqslant X \leqslant 900 + h) \approx 0,99$ à $10^{-3}$ près.
- La chaine de production a été réglée dans le but d'obtenir au moins 97 % de comprimés conformes. Afin d'évaluer l'efficacité des réglages, on effectue un contrôle en prélevant un échantillon de 1000 comprimés dans la production.
La taille de la production est supposée suffisamment grande pour que ce prélèvement puisse être assimilé à 1000 tirages successifs avec remise.
Le contrôle effectué a permis de dénombrer $53$ comprimés non conformes sur l'échantillon prélevé.
Ce contrôle remet-il en question les réglages faits par le laboratoire ? On pourra utiliser un intervalle de fluctuation asymptotique au seuil de 95 %.
Correction de l'exercice 2 (5 points)
Les parties A et B peuvent être traitées indépendamment.
Partie A
- la probabilité qu'une personne malade présente un test positif est $0,99$ ;
- la probabilité qu'une personne saine présente un test positif est $0,001$.
- Pour une maladie qui vient d'apparaître, le laboratoire élabore un nouveau test. Une étude statistique permet d'estimer que le pourcentage de personnes malades parmi la population d'une métropole est égal à 0,1 %.
On choisit au hasard une personne dans cette population et on lui fait subir le test.
On note $M$ l'évènement « la personne choisie est malade» et $T$ l'évènement « le test est positif » .- Traduire l'énoncé sous la forme d'un arbre pondéré.
- Démontrer que la probabilité $p(T)$ de l'évènement $T$ est égale à $1,989 \times 10^{-3}$. Calculons la probabilité de l'événement $T$.
- L'affirmation suivante est-elle vraie ou fausse ? Justifier la réponse. Affirmation : « Si le test est positif, il y a moins d'une chance sur deux que la personne soit malade » . On veut calculer la probabilité de l'événement « Sachant que le test est positif, la personne soit malade » . soit à calculer la probabilité conditionnelle $p_{T}\left (M\right )=\dfrac{p\left (T\cap M\right )}{p(T)}=\dfrac{0,001 \times 0,99}{0,1989 \times 10^{-3} }=\dfrac{990}{1989}=\dfrac{110}{221} \approx 0,498$ $p_{T}\left (M\right )\approx 0,498 $ et donc $p_{T}\left (M\right ) < \dfrac{1 }{2 }$
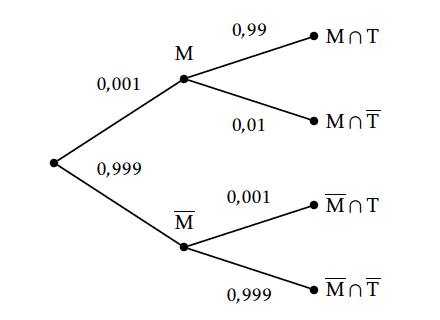
$T=\left (M\cap T \right )\cup \left (\overline{M}\cap T \right ) $. La formule des probabilités totales donne $$p(T)=p\left (M\cap T \right )+p \left (\overline{M}\cap T \right )=p(M)\times p_{M}(T)+p(\overline{M}) \times p_{\overline{M}}(T) $$ soit $p(T)= 0,001\times 0,99+ 0,999\times 0,001 =0,001989=1,989 \times 10^{-3}$
L'affirmation : « Si le test est positif, il y a moins d'une chance sur deux que la personne soit malade » est donc vraie. - Le laboratoire décide de commercialiser un test dès lors que la probabilité qu'une personne testée positivement soit malade est supérieure ou égale à $0,95$.
On désigne par $x$ la proportion de personnes atteintes d'une certaine maladie dans la population. À partir de quelle valeur de $x$ le laboratoire commercialise-t-il le test correspondant ?
Tout d'abord on représente la situation avec l'arbre de probabilité mis à jour :
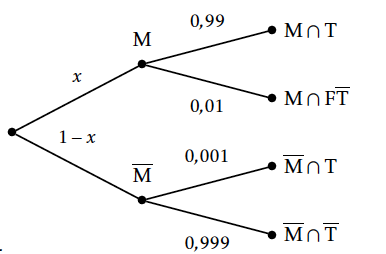
On cherche alors $x$ tel que $p_{T}\left (M\right )\geq 0,95$ $$p_{T}\left (M\right )=\dfrac{p\left (T\cap M\right )}{p(T)}$$ Calculons la probabilité de l'événement $T$. $T=\left (M\cap T \right )\cup \left (\overline{M}\cap T \right ) $.
La formule des probabilités totales donne $$p(T)=p\left (M\cap T \right )+p \left (\overline{M}\cap T \right )=p(M)\times p_{T}(C)+p(\overline{M}) \times p_{\overline{M}}(T) $$ soit $p(T)= x \times 0,99+ (1-x)\times 0,001 $ $$ \begin{array}{ l l l} p_{T}\left (M\right )\geq 0,95 & \iff \dfrac{ 0,99\times x } {x \times 0,99+ (1-x)\times 0,001} \geq 0,95 &\\ &\iff \dfrac{ 1000\times 0,99\times x }{1000\times \left (x \times 0,99+ (1-x)\times 0,001\right )} \geq 0,95 & \\ & \iff \dfrac{990x}{990x +1-x} \geq 0,95 & \\ & \iff \dfrac{990x}{989x +1 } \geq 0,95 & \\ & \iff 990 x \geq 0,95 \times (989x +1) & \text{ en multipliant par }(989x +1) > 0 \\ & \iff x\geq \dfrac{19}{1009} & \\ \end{array}$$
Le laboratoire décide de commercialiser un test dès que $x\geq \dfrac{19}{1009}$
Partie B
- Un comprimé est conforme si sa masse est comprise entre 890 et 920 mg.
On admet que la masse en milligrammes d'un comprimé pris au hasard dans la production peut être modélisée par une variable aléatoire $X$ qui suit la loi normale $\mathcal{N}\left(\mu,~\sigma^2\right)$, de moyenne $\mu = 900$ et d'écart-type $\sigma = 7$.- Calculer la probabilité qu'un comprimé prélevé au hasard soit conforme. On arrondira à $10^{-2}$. 2ND DISTR 2 NORMALCDF( 890 , 920,900 ,7)EXE
- Déterminer l'entier positif $h$ tel que $P(900 - h \leqslant X \leqslant 900 + h) \approx 0,99$ à $10^{-3}$ près. Posons $Z= \dfrac{X - \mu}{\sigma}=\dfrac{X - 900}{7}$ . La variable aléatoire $Z$ suit la loi normale centrée réduite.
$Normalcdf(890,920,900,7)\approx 0,921$
$P(890\leq X \leq 920)\approx 0,921$ à $ 10^{-3}$ près.
$Z$ suit la loi normale centrée réduite.
$ P(900 - h \leqslant X \leqslant 900 + h) \approx 0,99 \Leftrightarrow p\left(\dfrac{900 -h - 900}{7} \leqslant\dfrac{X - 900}{7} \leq \dfrac{900 +h - 900}{7} \right)\approx 0,99 \Leftrightarrow p \left( -\dfrac{h}{7} \leq Z \leqslant \dfrac{h}{7} \right) \approx 0,99 $. On doit donc avoir $$p \left( -\dfrac{h}{7} \leq Z \leqslant \dfrac{h}{7} \right) \approx 0,99 \Leftrightarrow 2 \pi\left(\dfrac{h}{7}\right) -1 \approx 0,99 \Longleftrightarrow \pi\left(\dfrac{h}{7}\right) \approx \dfrac{1,99}{2} \Longleftrightarrow \dfrac{h}{7}\approx \pi^{-1}(0, 995)\Leftrightarrow h\approx 18,030 $$ La valeur attendue de $h$ est donc $ 18,030 $.
- La chaine de production a été réglée dans le but d'obtenir au moins 97 % de comprimés conformes. Afin d'évaluer l'efficacité des réglages, on effectue un contrôle en prélevant un échantillon de 1000 comprimés dans la production.
La taille de la production est supposée suffisamment grande pour que ce prélèvement puisse être assimilé à 1000 tirages successifs avec remise.
Le contrôle effectué a permis de dénombrer $53$ comprimés non conformes sur l'échantillon prélevé.
Ce contrôle remet-il en question les réglages faits par le laboratoire ? On pourra utiliser un intervalle de fluctuation asymptotique au seuil de 95 %. Remarque : l'énoncé sous-entend que la taille de la production est supposée suffisamment grande pour que ce prélèvement puisse être assimilé à 1000 tirages successifs avec remise et donc le tirage de l'échantillon puisse se faire dans les conditions d'application d'une loi binomiale... il faudrait toujours le préciser.
Ici $ p = 0,97, n = 1 000$,donc on a bien $n \geq 30, np =970 \geq 5, n(1- p)=30 \geq 5$ et pour $\alpha = 0,05$, on a $u_{\alpha} \approx 1,96$. L'intervalle $\tilde{I_n}=\left [p-1,96\sqrt{\dfrac{pq}{n}};p+1,96\sqrt{\dfrac{pq}{n}}\right ]=\left [0,97-1,96\sqrt{\dfrac{0,97\times 0,03}{1000}};
0,97+1,96\sqrt{\dfrac{0,97\times 0,03}{1000}}\right ]\approx [0,959 ; 0,981]$ de fluctuation asymptotique au seuil de 0,95 est donc environ $[0,959 ; 0,981]$.
Sur 1000 comprimés, 53 sont non conformes et donc 947 sont conformes, soit une fréquence de $\dfrac{947}{1 000} = 0,947$ : cette fréquence n'appartient pas à l'intervalle de fluctuation de fluctuation asymptotique au seuil de 95 %.
Les réglage faits par le laboratoire ne sont donc pas convenables.
Exercice 3 5 points
On désigne par (E) l'équation \[z^4 + 4z^2 + 16 = 0\] d'inconnue complexe $z$.
- Résoudre dans $\mathbb{C}$ l'équation $Z^2 +4Z + 16 = 0$.
Écrire les solutions de cette équation sous une forme exponentielle. - On désigne par $a$ le nombre complexe dont le module est égal à 2 et dont un argument est égal à $\dfrac{\pi}{3}$.
Calculer $a^2$ sous forme algébrique. En déduire les solutions dans $\mathbb{C}$ de l'équation $z^2 = - 2 + 2\text{i}\sqrt{3}$.
On écrira les solutions sous forme algébrique. - Restitution organisée de connaissances
On suppose connu le fait que pour tout nombre complexe $z = x + \text{i}y$ où $x \in \mathbb{R}$ et $y \in \mathbb{R}$, le conjugué de $z$ est le nombre complexe $z$ défini par $z = x - \text{i} y$. Démontrer que :- Pour tous nombres complexes $z_{1}$ et $z_{2}$, $\overline{ z_{1} \times z_{2}}=\overline{z_{1} } \times\overline{ z{2}} $.
- Pour tout nombre complexe $z$ et tout entier naturel non nul $n,\: \overline{z^{n}} = \left(\overline{z}\right)^n$.
- Démontrer que si $z$ est une solution de l'équation (E) alors son conjugué $\overline{z}$ est également une solution de (E).
En déduire les solutions dans $\mathbb{C}$ de l'équation (E). On admettra que (E) admet au plus quatre solutions.
Correction de l'exercice 3 (5 points)
On désigne par (E) l'équation \[z^4 + 4z^2 + 16 = 0\] d'inconnue complexe $z$.
- Résoudre dans $\mathbb{C}$ l'équation $Z^2 +4Z + 16 = 0$.
Écrire les solutions de cette équation sous une forme exponentielle. - On désigne par $a$ le nombre complexe dont le module est égal à 2 et dont un argument est égal à $\dfrac{\pi}{3}$.
Calculer $a^2$ sous forme algébrique. En déduire les solutions dans $\mathbb{C}$ de l'équation $z^2 = - 2 + 2\text{i}\sqrt{3}$.
On écrira les solutions sous forme algébrique. $$a^2=\left(2e^{i\frac{ \pi}{3}} \right)^2=4 e^{i\frac{2\pi}{3}} =Z_1= -2 + 2i\sqrt 3 $$ $$z^2 = - 2 + 2\text{i}\sqrt{3} \iff z^2 = a^2 \iff z^2 - a^2 =0 \iff (z- a)(z+a)=0\iff z=a \text{ ou } z=-a $$ les solutions dans $\mathbb{C}$ de l'équation $z^2 = - 2 + 2\text{i}\sqrt{3}$ sont $a=2e^{i\frac{ \pi}{3}}=2\left( \dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)=1+ i \sqrt{3}$ et $-a=-1- i \sqrt{3}$
- Restitution organisée de connaissances
On suppose connu le fait que pour tout nombre complexe $z = x + \text{i}y$ où $x \in \mathbb{R}$ et $y \in \mathbb{R}$, le conjugué de $z$ est le nombre complexe $z$ défini par $z = x - \text{i} y$. Démontrer que :- Pour tous nombres complexes $z_{1}$ et $z_{2}$, $\overline{ z_{1} \times z_{2} }=\overline{z_{1} } \times\overline{ z{2}} $. $$\begin{array}{rl } \text{Posons } z_1 &= a+i b \\ z_2 &= c+i d \\ z_1 . z_2&=(a+ib).(c+id)\\ & =(ac-bd)+i(ad+bc)\\ \text{Ainsi } \overline{ z_1 . z_2}&=(ac-bd)-i(ad+bc)\\ \text{Par ailleurs } \overline{ z_1 }.\overline{ z_2}&=(a-ib).(c-id)\\ &= (ac-bd)-i(ad+bc)\\ \end{array} $$ $$\text{ On a donc bien } \overline{ z_{1} \times z_{2} }= \overline{z_{1} } \times \overline{ z{2}} $$
- Pour tout nombre complexe $z$ et tout entier naturel non nul $n,\: \overline{z^{n}} = \left(\overline{z}\right)^n$. On note $\mathcal{P}(n)$ la propriété : $~\overline{z^{n}} = \left(\overline{z}\right)^n$.
- Initialisation :Au rang 1; on a $~\overline{z^{1}} = \overline{z }=\left(\overline{z}\right)^1$, ce qui prouve que $\mathcal{P}(1)$ est vrai.
- Hérédité :Soit $p\geq 1$, on suppose que: $~\overline{z^{p}} = \left(\overline{z}\right)^p \;\text{ HR }$.
On doit prouver que : $~\overline{z^{p+1}} = \left(\overline{z}\right)^{p+1} $
$$\begin{array}{rl l } ~\overline{z^{p+1}}& =\overline{z^{p } \times z}& \\ & = \overline{z^{p }} \times \overline{z} & \text{D'après la propriété ci-dessus ! }\\ & = \overline{z}^p \times \overline{z} & \text{ D'après HR ! }\\ &= \left(\overline{z}\right)^{p+1} \\ \end{array} $$ - Conclusion :La propriété est vraie au rang 1, pour $k\geq 1 $ ; $\mathcal{P}( k ) $ vraie entraîne $\mathcal{P}( k+1 ) $ vraie,le principe de récurrence s'applique et donc pour tout $n \geq 1$: $~\overline{z^{n}} = \left(\overline{z}\right)^n$
- Démontrer que si $z$ est une solution de l'équation (E) alors son conjugué $\overline{z}$ est également une solution de (E).
En déduire les solutions dans $\mathbb{C}$ de l'équation (E). On admettra que (E) admet au plus quatre solutions. si $z$ est une solution de l'équation (E) alors : $$\begin{array}{ l l }z^4 + 4z^2 + 16 = 0& \\ \overline{z^4 + 4z^2 + 16} = 0& \\ \overline{z^4} + \overline{4z^2} + \overline{16} = 0& \text{ car }\overline{z+z'} =\overline{z} +\overline{z'} \\ \overline{z} ^4+ 4\overline{z} ^2+ 16 = 0& \text{ car }\overline{z^4} =\overline{z}^4 \ldots \\ \\ \end{array}$$ Ainsi si $z$ est une solution de l'équation (E) alors : alors son conjugué $\overline{z}$ est également une solution de (E).
On calcule $\Delta = 16-4\times 16 =-48$. Comme $\Delta< 0$, l'équation a deux racines complexes conjuguées : $$Z_1=\dfrac{-b+i\sqrt{-\Delta}}{2a} = \dfrac{-4+i\sqrt{48}}{2 } = \dfrac{-4+i4\sqrt{3}}{2 } = -2 + 2i\sqrt 3 \text { et } Z_2=\overline{Z_1}= -2 - 2i\sqrt 3 $$ $$ \mathcal{S} =\{ -2 + 2i\sqrt 3; -2 - 2i\sqrt 3 \}$$ Forme exponentielle des solutions: $$ Z_1 =-2 + 2i\sqrt 3= 4 \left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)=4 \left(\cos\left(\dfrac{2\pi}{3}\right)+i\sin\left(\dfrac{2\pi}{3}\right)\right)$ $$ Z_1 =4e^{i\frac{2\pi}{3}} \text{ et } Z_2 =4e^{-i\frac{2\pi}{3}}$$
Comme $a$ et $-a$ sont deux solutions de (E); on déduit que leurs conjugués $\overline{a}=1-i\sqrt 3 $ et $-\overline{a} =-1+i\sqrt 3 $ sont aussi soltions de (E). En conclusion (E) a pour ensemble de solutions : $$ \mathcal{S} =\{ 1 + i\sqrt 3; -1 - i\sqrt 3;1-i\sqrt 3;-1+i\sqrt 3 \}$$
Exercice 4 5 points
Dans l'espace, on considère un tétraèdre ABCD dont les faces ABC, ACD et ABD sont des triangles rectangles et isocèles en A. On désigne par E, F et G les milieux respectifs des côtés [AB], [BC] et [CA]. On choisit AB pour unité de longueur et on se place dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AC}}, \vec{\text{AD}}\right)$ de l'espace.
- On désigne par $\mathcal{P}$ le plan qui passe par A et qui est orthogonal à la droite (DF). On note H le point d'intersection du plan $\mathcal{P}$ et de la droite (DF).
- Donner les coordonnées des points D et F.
- Donner une représentation para métrique de la droite (DF).
- Déterminer une équation cartésienne du plan $\mathcal{P}$.
- Calculer les coordonnées du point H.
- Démontrer que l'angle $\widehat{\text{EHG}}$ est un angle droit.
- On désigne par $M$ un point de la droite (DF) et par $t$ le réel tel que $\vec{\text{D}M} = t\vec{\text{DF}}$. On note $\alpha$ la mesure en radians de l'angle géométrique $\widehat{\text{E}M\text{G}}$. Le but de cette question est de déterminer la position du point $M$ pour que $\alpha$ soit maximale.
- Démontrer que $M\text{E}^2 = \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}$.
- Démontrer que le triangle $M$EG est isocèle en $M$. En déduire que $M\text{E}\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{1}{2\sqrt{2}}$.
- Justifier que $\alpha$ est maximale si et seulement si $\sin \left(\dfrac{\alpha}{2} \right)$ est maximal. En déduire que $\alpha$ est maximale si et seulement si $M\text{E}^2$ est minimal.
- Conclure.
Correction de l'exercice 4 5 points
On choisit AB pour unité de longueur et on se place dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AC}}, \vec{\text{AD}}\right)$ de l'espace.
- On désigne par $\mathcal{P}$ le plan qui passe par A et qui est orthogonal à la droite (DF). On note H le point d'intersection du plan $\mathcal{P}$ et de la droite (DF).
- Donner les coordonnées des points D et F. Dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AC}}, \vec{\text{AD}}\right)$ on a D $(0\,, 0\,,1)$ et F milieu de B $(1\,, 0\,,0)$ C $(0\,, 1\,,0)$ donc F a pour coordonnées $(\dfrac{1+0}{2}\,,\dfrac{0+1}{2}\,,0)=(\dfrac{1}{2}\,,\dfrac{1}{2}\,,0)$
- Donner une représentation para métrique de la droite (DF). Ainsi $ \vec{\text{DF}} $ a pour coordonnées $\left (\dfrac{1}{2}-0\,,\dfrac{1}{2}-0\,,1-0\right )$ $M(x~;~y~;~z) \in (DF)$ vérifie $\overrightarrow{DM}=t \overrightarrow{DF}$, on a donc: $ \left\lbrace \begin{array}{l l} x-0 &= \dfrac{1}{2}t\\ y-0 &= \dfrac{1}{2}t\\ z-1 &= t \end{array} \right. \iff \left\lbrace \begin{array}{l l} x&= \dfrac{1}{2}t\\ y&= \dfrac{1}{2}t\\ z&= 1-t \end{array} \right.$
- Déterminer une équation cartésienne du plan $\mathcal{P}$. $\mathcal{P}$ a pour vecteur normal $ \vec{\text{DF}} $ car $\mathcal{P}$ est orthogonal à la droite (DF).
- Calculer les coordonnées du point H. $H(x~;~y~;~z) \in (DF \cap \mathcal{P})$ vérifie le système : $ \left\lbrace \begin{array}{l l} x+y-2z&=0 \; (1)\\ x &= \dfrac{1}{2}t\\ y &= \dfrac{1}{2}t\\ z &= 1-t \end{array} \right.$ $(1)\iff \dfrac{1}{2}t +\dfrac{1}{2}t-2(1-t)=0 \iff 3t =2 \iff t=\dfrac{2}{3}$
- Démontrer que l'angle $\widehat{\text{EHG}}$ est un angle droit. On a $\overrightarrow{EH}\begin{pmatrix}\dfrac{1}{3}-\dfrac{1}{2}\\\dfrac{1}{3}\\\dfrac{1}{3}\end{pmatrix} =\begin{pmatrix}-\dfrac{1}{6}\\\dfrac{1}{3}\\\dfrac{1}{3}\end{pmatrix}$ et $\overrightarrow{EH}\begin{pmatrix}\dfrac{1}{3}\\\dfrac{1}{3}-\dfrac{1}{2}\\\dfrac{1}{3}\end{pmatrix} =\begin{pmatrix}\dfrac{1}{3}\\-\dfrac{1}{6}\\\dfrac{1}{3}\end{pmatrix}$ $$ \overrightarrow{EH}\cdot\overrightarrow{GH}=-\dfrac{1}{6}\times \dfrac{1}{3}+\left(-\dfrac{1}{6}\times \dfrac{1}{3}\right)+\dfrac{1}{3}\times\dfrac{1}{3}=-\dfrac{1}{18}-\dfrac{1}{18}+\dfrac{1}{9}=0$$ Ainsi $\overrightarrow{EH}\cdot \overrightarrow{GH}=0$, ce qui prouve que l'angle $\widehat{\text{EHG}}$ est un angle droit.
- On désigne par $M$ un point de la droite (DF) et par $t$ le réel tel que $\vec{\text{D}M} = t\vec{\text{DF}}$. On note $\alpha$ la mesure en radians de l'angle géométrique $\widehat{\text{E}M\text{G}}$. Le but de cette question est de déterminer la position du point $M$ pour que $\alpha$ soit maximale.
- Démontrer que $M\text{E}^2 = \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}$. $M$ un point de la droite (DF) et par $t$ le réel tel que $\vec{\text{D}M} = t\vec{\text{DF}}$ a pour coordonnées $(x\,,y\,,z)$ tels que : $ \left\lbrace \begin{array}{l l} x &= \dfrac{1}{2}t\\ y &= \dfrac{1}{2}t\\ z &= 1-t \end{array} \right.$
- Démontrer que le triangle $M$EG est isocèle en $M$. En déduire que $M\text{E}\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{1}{2\sqrt{2}}$. On a G milieu de A $(0\,, 0\,,0)$ C $(0\,, 1\,,0)$ donc G a pour coordonnées $(0\,,\dfrac{1}{2}\,,0)$ $$\overrightarrow{MG}\begin{pmatrix}\dfrac{1}{2}t\\ \dfrac{1}{2}t -\dfrac{1}{2}\\1-t\end{pmatrix} =\begin{pmatrix} \dfrac{1}{2}(1-t)\\ -\dfrac{1}{2}t\\t-1\end{pmatrix}$$ $$\text{ Ainsi : }$$ $$\begin{array}{l l} MG^2&=\left(\dfrac{1}{2}t\right)^2+\left( \dfrac{1}{2}(t-1)\right)^2+\left(1-t\right)^2 \\ &= \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}\\ &= ME^2\\ \end{array}$$ Ayant $MG^2=ME^2$; on a prouvé que $ME=MG$ et donc le triangle $M$EG est isocèle en $M$.
- Justifier que $\alpha$ est maximale si et seulement si $\sin \left(\dfrac{\alpha}{2} \right)$ est maximal. En déduire que $\alpha$ est maximale si et seulement si $M\text{E}^2$ est minimal. On appelle $K$ le milieu de $[EG]$. La droite $(MK)$ est donc une hauteur et une bissectrice du triangle $MEG$ et $\widehat{EMK} = \dfrac{\alpha}{2}$.
- Conclure.
- Première méthode : Pour déterminer le minimum de $ME$ on va trouver la valeur de $t$ telle que $\dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}$ soit minimal.
Il s’agit de trouver l’abscisse du sommet de la parabole correspondante :
$$x_S = \dfrac{-b}{2a} = \dfrac{5}{6}$$
Par conséquent les coordonnées du point $M$ cherché sont $\left( \dfrac{5}{12};\dfrac{5}{12};\dfrac{1}{6} \right)$. - Deuxième méthode : on étudie les variation de $\phi : t \mapsto : \dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}$
$\phi$ est dérivable sur $\mathbb{R}$ et $$\phi '(t)=\dfrac{3}{2}\times 2t -\dfrac{5}{2} =3t - \dfrac{5}{2}$$ $$\phi '(t) >0 \iff 3t - \dfrac{5}{2} >0 \iff t>\dfrac{5}{6} $$
d' où le tableau de variation de $\phi$ sur $\mathbb{R}$ :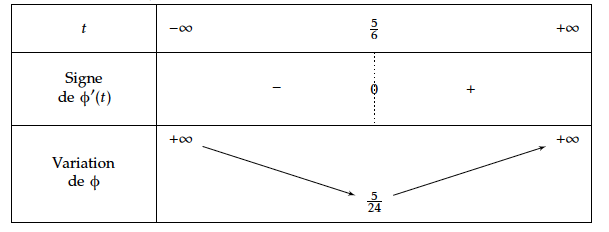
$$\phi \left (\frac{5}{24}\right) =\frac{3}{2}\times \frac{25}{36} -\frac{5}{2}\times \frac{5}{6} +\frac{5}{4}=\frac{5}{24}$$ Par conséquent les coordonnées du point $M$ cherché sont $\left( \dfrac{5}{12};\dfrac{5}{12};\dfrac{1}{6} \right)$.
On a alors $\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME} =\dfrac{\frac{1}{2\sqrt 2}}{\sqrt{\frac{5}{24}}}=\sqrt{\dfrac{3}{5}}$
On déduit $\dfrac{\alpha}{2}=\sin ^{-1} \left (\sqrt{\dfrac{3}{5}}\right ) $
Le maximum de l'angle $\alpha$ est donc $2\sin ^{-1} \left (\sqrt{\dfrac{3}{5}}\right )\approx 101,5 ^{\circ}$
- Première méthode : Pour déterminer le minimum de $ME$ on va trouver la valeur de $t$ telle que $\dfrac{3}{2}t^2-\dfrac{5}{2}t+\dfrac{5}{4}$ soit minimal.
$$\overrightarrow{ME}\begin{pmatrix}\dfrac{1}{2}-\dfrac{1}{2}t\\0-\dfrac{1}{2}t\\t-1\end{pmatrix} =\begin{pmatrix} \dfrac{1}{2}(1-t)\\ -\dfrac{1}{2}t\\t-1\end{pmatrix}$$ $$\text{ Ainsi : }$$ $$\begin{array}{l l} ME^2&=\left( \dfrac{1}{2}(1-t)\right)^2+\left(-\dfrac{1}{2}t\right)^2+\left(t-1\right)^2 \\ &= \dfrac{1}{4}(t-1)^2+\dfrac{1}{4}t^2+(t-1)^2\\ &= \dfrac{5}{4}(t-1)^2+\dfrac{1}{4}t^2\\ &= \dfrac{5}{4}(t^2-2t+1)+\dfrac{1}{4}t^2\\ &= \dfrac{3}{2}t^2 - \dfrac{5}{2}t + \dfrac{5}{4}\\ \end{array}$$
Dans le triangle $MEG$ rectangle en $K$ on a : $\sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME}$
Or $EK = \dfrac{EG}{2} = \dfrac{\sqrt{0,5}}{2} = \dfrac{1}{2\sqrt{2}}$.
Par conséquent :
$$ \sin \left(\dfrac{\alpha}{2} \right) = \dfrac{EK}{ME} \Leftrightarrow ME \sin \left(\dfrac{\alpha}{2} \right) = \dfrac{1}{2\sqrt{2}}$$.
$~$
Première méthode : La fonction $\sin$ est strictement croissante sur $\left[0;\dfrac{\pi}{2}\right]$.
Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal.
$~$
Deuxième méthode : Les fonctions $\alpha \mapsto \alpha $ et $\alpha \sin\left( \dfrac{\alpha}{2} \right)$ sont dérivables sur $\mathbb{R}$.
$ \left(\sin\left( \dfrac{\alpha}{2} \right) \right)’ = \dfrac{\alpha’}{2} \cos \left( \dfrac{\alpha}{2} \right) $.
$\alpha$ ne prend des valeurs que dans $[0;\pi]$ donc $\cos \left( \dfrac{\alpha}{2} \right) \geq 0$ Par conséquent :
le signe de $\left(sin\left( \dfrac{\alpha}{2} \right) \right)’ $ = le signe de $\alpha’$.
Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal.
$~$
$~$
$~$
Le produit $ME \sin \left(\dfrac{\alpha}{2} \right) $ est constant.
Par conséquent $\alpha$ maximale $\Leftrightarrow \sin \left( \dfrac{\alpha}{2} \right)$ maximal $\Leftrightarrow ME$ minimal.
$~$
Ainsi $\mathcal{P}$ a une équation cartésienne du type $$ \dfrac{1}{2}x+ \dfrac{1}{2}y-z+d=0$$ $A (0\,,0\,,0\,,0)\in \mathcal{P}$ donc $d=0$.
$\mathcal{P}$ admet pour équation cartésienne $\dfrac{1}{2}x+\dfrac{1}{2}y-z=0$ $\mathcal{P}$ admet pour équation cartésienne $x+y-2z=0$
En reportant $t=\dfrac{2}{3}$ dans la représentation paramétrique de la droite (DF) on obtient : H a pour coordonnées $\left(\dfrac{1}{3}\,,\dfrac{1}{3}\,,\dfrac{1}{3}\right)$
Spécialité 5 points
Un pisciculteur dispose de deux bassins A et B pour l'élevage de ses poissons. Tous les ans à la même période :
- il vide le bassin B et vend tous les poissons qu'il contenait et transfère tous les poissons du bassin A dans le bassin B ;
- la vente de chaque poisson permet l'achat de deux petits poissons destinés au bassin A.
- Par ailleurs, le pisciculteur achète en plus $200$ poissons pour le bassin A et $100$ poissons pour le bassin B.
Pour tout entier naturel $n$ supérieur ou égal à 1, on note respectivement $a_{n}$ et $b_{n}$ les effectifs de poissons des bassins A et B au bout de $n$ années.
En début de première année, le nombre de poissons du bassin A est $a_{0} = 200$ et celui du bassin B est $b_{0} = 100$.
- Justifier que $a_{1} = 400$ et $b_{1} = 300$ puis calculer $a^2$ et $b^2$.
- On désigne par $A$ et $B$ les matrices telles que $A = \begin{pmatrix}0&2\\1&0\end{pmatrix}$ et $B = \begin{pmatrix}200\\100\end{pmatrix}$ et pour tout entier naturel $n$, on pose $X_{n} = \begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$.
- Expliquer pourquoi pour tout entier naturel $n$, $X_{n+1} = AX_{n} + B$.
- Déterminer les réels $x$ et $y$ tels que $\begin{pmatrix}x\\y\end{pmatrix} = A\begin{pmatrix}x\\y\end{pmatrix} + B$.
- Pour tout entier naturel $n$, on pose $Y_{n} = \begin{pmatrix}a_{n} + 400\\ b_{n} + 300\end{pmatrix}$. Démontrer que pour tout entier naturel $n,\:\: Y_{n+1} = AY_{n}$.
- Pour tout entier naturel $n$, on pose $Z_{n} = Y_{2n}$.
- Démontrer que pour tout entier naturel $n,\: Z_{n+1} = A^2 Z_{n}$. En déduire que pour tout entier naturel $n, Z_{n+1} = 2Z_{n}$.
- On admet que cette relation de récurrence permet de conclure que pour tout entier naturel $n$, \[Y_{2n} = 2Z_{n}.\] En déduire que $Y_{2n + 1} = 2^nY_{1}$ puis démontrer que pour tout entier naturel $n$, \[a_{2n} = 600 \times 2^n - 400\quad \text{et}\quad a_{2n+1} = 800 \times 2^n - 400.\]
- Le bassin A a une capacité limitée à 10 000 poissons.
- On donne l'algorithme suivant. $$\begin{array} {|l |l|}\hline \text{ Variables : } & a, p \text{ et } n \text{sont des entiers naturels.}\\ \text{Initialisation :}& \text{ Demander à l'utilisateur la valeur de } p.\\ \text{ Traitement : } &\text{ Si } p \text{ est pair }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p}{2}\\ \text{ Affecter à a la valeur } 600 \times 2^n - 400.\\ \end{array}\\ &\text{ Sinon }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p - 1}{2}\\ \text{ Affecter à } a \text{ la valeur } 800 \times 2^n - 400.\\ \end{array}\\ &\text{ Fin de Si. }\\ \text{ Sortie : } & \text{ Afficher } a.\\ \hline \end{array}$$ Que fait cet algorithme ? Justifier la réponse.
- Écrire un algorithme qui affiche le nombre d'années pendant lesquelles le pisciculteur pourra utiliser le bassin A.
Correction de l'exercice de Spécialité 5 points
- il vide le bassin B et vend tous les poissons qu'il contenait et transfère tous les poissons du bassin A dans le bassin B ;
- la vente de chaque poisson permet l'achat de deux petits poissons destinés au bassin A.
- Par ailleurs, le pisciculteur achète en plus $200$ poissons pour le bassin A et $100$ poissons pour le bassin B.
En début de première année, le nombre de poissons du bassin A est $a_{0} = 200$ et celui du bassin B est $b_{0} = 100$.
- Justifier que $a_{1} = 400$ et $b_{1} = 300$ puis calculer $a^2$ et $b^2$.
- On désigne par $A$ et $B$ les matrices telles que $A = \begin{pmatrix}0&2\\1&0\end{pmatrix}$ et $B = \begin{pmatrix}200\\100\end{pmatrix}$ et pour tout entier naturel $n$, on pose $X_{n} = \begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$.
- Expliquer pourquoi pour tout entier naturel $n$, $X_{n+1} = AX_{n} + B$.
- Déterminer les réels $x$ et $y$ tels que $\begin{pmatrix}x\\y\end{pmatrix} = A\begin{pmatrix}x\\y\end{pmatrix} + B$. On cherche les valeurs de $(x;y)$ telles que :
- Pour tout entier naturel $n$, on pose $Y_{n} = \begin{pmatrix}a_{n} + 400\\ b_{n} + 300\end{pmatrix}$. Démontrer que pour tout entier naturel $n,\:\: Y_{n+1} = AY_{n}$.
$$\begin{array} AX_n+B &= \begin{pmatrix}2b_n \\\\a_n \end{pmatrix} + \begin{pmatrix}200\\\\100 \end{pmatrix} \\\\
&= \begin{pmatrix} 2b_n+200 \\\\a_n + 100 \end{pmatrix} \\\\
&=X_{n+1}
\end{array}$$
$$\begin{array}{cccc} \begin{cases} x=2y+200 \\\\y=x+100 \end{cases} & \Leftrightarrow \begin{cases} x=2y+200 \\\\y=2y+200+100 \end{cases} \\\\ & \Leftrightarrow \begin{cases} x=2y+200 \\\\ y=-300\end{cases} \\\\ & \Leftrightarrow \begin{cases} x=-400 \\\\ y=-300\end{cases} \end{array}$$
$$\begin{array} Y_{n+1} &= \begin{pmatrix} a_{n+1}+400 \\\\b_{n+1}+300 \end{pmatrix} \\\\
&= \begin{pmatrix} 2b_n+200 + 400 \\\\a_n+100 + 300 \end{pmatrix} \\\\
&=\begin{pmatrix} 2(b_n + 300) \\\\a_n + 400 \end{pmatrix} \\\\
&=AY_n
\end{array}$$ - Pour tout entier naturel $n$, on pose $Z_{n} = Y_{2n}$.
- Démontrer que pour tout entier naturel $n,\: Z_{n+1} = A^2 Z_{n}$. En déduire que pour tout entier naturel $n, Z_{n+1} = 2Z_{n}$.
- On admet que cette relation de récurrence permet de conclure que pour tout entier naturel $n$, \[Y_{2n} = 2Z_{n}.\] En déduire que $Y_{2n + 1} = 2^nY_{1}$ puis démontrer que pour tout entier naturel $n$, \[a_{2n} = 600 \times 2^n - 400\quad \text{et}\quad a_{2n+1} = 800 \times 2^n - 400.\] $Y_{2n+1} = AY_{2n}=2^nAY_0= 2^nY_1$
$Z_{n+1} = Y_{2(n+1)} = Y_{2n+2} = AY_{2n+1} = A^2Y_{2n} = A^2Z_n$
$~$
On a $A^2 = 2I$ où $I$ est la matrice identité.
Par conséquent $Z_{n+1}=2Z_n$.
Or $Y_0 = \begin{pmatrix} 600\\\\400 \end{pmatrix}$ donc $Y_{2n} = \begin{pmatrix} a_{2n} + 400\\\\b_{2n}+300 \end{pmatrix} = 2^n \begin{pmatrix} 600\\\\400 \end{pmatrix}$
Par conséquent $a_{2n} = 600 \times 2^n – 400$
$~$
$Y_1 = \begin{pmatrix} 800\\\\600 \end{pmatrix}$ donc $Y_{2n+1} = \begin{pmatrix} a_{2n+1} + 400\\\\b_{2n+1}+300 \end{pmatrix} = 2^n \begin{pmatrix} 800\\\\600 \end{pmatrix}$
Par conséquent $a_{2n} = 800 \times 2^n – 400$ - Le bassin A a une capacité limitée à 10 000 poissons.
- On donne l'algorithme suivant. $$\begin{array} {|l |l|}\hline \text{ Variables : } & a, p \text{ et } n \text{sont des entiers naturels.}\\ \text{Initialisation :}& \text{ Demander à l'utilisateur la valeur de } p.\\ \text{ Traitement : } &\text{ Si } p \text{ est pair }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p}{2}\\ \text{ Affecter à a la valeur } 600 \times 2^n - 400.\\ \end{array}\\ &\text{ Sinon }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p - 1}{2}\\ \text{ Affecter à } a \text{ la valeur } 800 \times 2^n - 400.\\ \end{array}\\ &\text{ Fin de Si. }\\ \text{ Sortie : } & \text{ Afficher } a.\\ \hline \end{array}$$ Que fait cet algorithme ? Justifier la réponse.
- Écrire un algorithme qui affiche le nombre d'années pendant lesquelles le pisciculteur pourra utiliser le bassin A.
Si $p$ est pair alors $p = 2k$ par conséquent, dans l’algorithme, $n=k$ et on calcule $a_{2k}=a_p$ d’après la question précédente.
Si $p$ est impaire alors $p=2k+1$ par conséquent, dans l’algorithme, $n= \dfrac{p-1}{2} = k$ et on calcule $a_{2k+1} = a_p$d’après la question précédente.
Dans tous les cas on calcule la population du bassin A au bout de $p$ années.$$\begin{array} {|l |l|}\hline \text{ Variables : } & a, p \text{ et } n \text{sont des entiers naturels.}\\ \text{Initialisation :}& p \text{ prend la valeur } 0.\\ & a \text{ prend la valeur } 200.\\ \text{ Traitement : } & \\ & \text{ Tant que : } a\leq 10 000 \\ & p \text{ prend la valeur } p+1 \\ \text{ Traitement : } &\text{ Si } p \text{ est pair }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p}{2}\\ \text{ Affecter à a la valeur } 600 \times 2^n - 400.\\ \end{array} \\ &\text{ Sinon }\\ &\begin{array}{|l} \text{ Affecter à } n \text{ la valeur } \dfrac{p - 1}{2}\\ \text{ Affecter à } a \text{ la valeur } 800 \times 2^n - 400.\\ \end{array}\\ &\text{ Fin de Si. }\\ & \text{ Fin de Tant que. } \\ \text{ Sortie : } & \text{ Afficher } p.\\ \hline \end{array}$$
On a $a-1 = 2b_0+200 = 400$ et $b_1 = a_0 + 100 = 300$
$~$
$a_2=2b_1+200 = 800$ et $b_2 = a_1 + 100 = 400$
On a donc $a_{n+1} = 2b_n+200$ et $b_{n+1}=a_n+100$
- Vues: 23016
