Métropole—La Réunion STI2D & STL 6 septembre 2018 - Exercice 3
Page 5 sur 8
Exercice 3 6 points
Une société d'extraction de gravier reçoit une commande de 550000 tonnes de gravier pour la construction d'un tronçon d'autoroute. Pour satisfaire cette commande, elle exploite un nouveau gisement de pierre.
Le responsable a recensé les masses journalières de gravier extraites de ce gisement au cours de son exploitation. La tendance observée et son expérience professionnelle le conduisent à modéliser la masse journalière de gravier extraite, exprimée en tonnes, par la fonction $f$ définie sur l'intervalle $[0~;~600]$ par : \[f(x) = \left(0,2x^2 + 30x\right)\text{e}^{- 0,01x}\] où $x$ désigne le temps écoulé en jours depuis le début de l'exploitation du gisement.
Partie A
-
- Démontrer que, pour tout $x$ de l'intervalle $[0~;~600]$, \[f'(x) = \left(- 0,002x^2 + 0,1x + 30\right)\text{e}^{- 0,01x}.\]
- Vérifier que, pour tout $x$ de l'intervalle $[0~;~600]$, \[f'(x) = 0,002(- x + 150)(x + 100)\text{e}^{- 0,01x}\]
-
- Étudier le signe de $f'(x)$ sur l'intervalle $[0~;~600]$.
- Dresser le tableau de variations de $f$ sur l'intervalle $[0~;~600]$.
- En déduire au bout de combien de jours la masse journalière de gravier extraite sera maximale. Quelle est alors cette masse maximale, en tonnes ?
- La courbe représentative de la fonction $f$ dans un repère orthogonal est donnée ci-dessous :
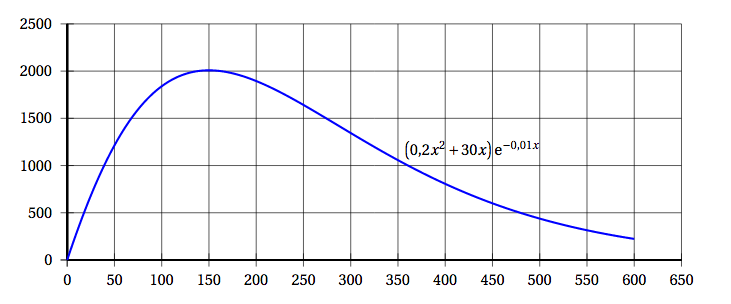
Après avoir atteint son maximum, la masse journalière de gravier extraite diminue. Déterminer graphiquement au bout de combien de jours elle deviendra alors inférieure à 1000 tonnes. Répondre avec la précision permise par le graphique.
Partie B
Un logiciel de calcul formel a permis d'obtenir les résultats suivants:
-
- Que représente le résultat fourni par le logiciel en ligne 2 ?
- Une valeur approchée de la masse totale de gravier extraite, en tonnes, entre le début de l'exploitation et le 600 ème jour d'exploitation est donnée par : \[I= \displaystyle\int_0^{600} f(x)\:\text{d}x.\] La commande pourra-t-elle être satisfaite au bout de $600$ jours ?
- Le responsable du chantier d'extraction estime que la commande sera satisfaite au bout de $400$ jours. Qu'en pensez-vous ? Justifier la réponse par un calcul.
Correction Exercice 3
- Vues: 19225
