Métropole—La Réunion STI2D & STL 6 septembre 2018 - Correction Exercice 1
Page 2 sur 8
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
Indiquer sur la copie le numéro de la question et la réponse correspondante choisie.
- Une forme exponentielle du nombre complexe $- 3 + \text{i}\sqrt{3}$ est :
- $- 2 \sqrt{3}\text{e}^{-\text{i}\frac{\pi}{6}}$
- $2\sqrt{3}\text{e}^{\text{i}\frac{\pi}{6}}$
- $2 \sqrt{3}\text{e}^{\text{i}\frac{5\pi}{6}}$
- $\sqrt{12}\text{e}^{- \text{i}\frac{5\pi}{6}}$
$z= - 3 + \text{i}\sqrt{3}$ $$\begin{array}{cc} \text{ Module} & \text{ Argument }\\ \begin{array}{rl|rl} |z |&=\sqrt{a^2+b^2} \\ & =\sqrt{ 3^2+\sqrt{3}^2}\\ &=\sqrt 12\\ &= 2\sqrt 3 \end{array}& \left\lbrace \begin{array}{l} \cos \theta=\frac{a}{r}~=\frac{-3}{2\sqrt 3}= -\frac{\sqrt 3}{2}\\ ~\sin \theta=\frac{b}{r}~= \frac{\sqrt 3}{2\sqrt 3}= \frac{1}{2} \end{array} \right.\\ &\text{ Donc } \theta = \frac{5\pi}{6} \text{ convient } \end{array}$$ $$z= - 3 + \text{i}\sqrt{3}= 2\sqrt 3 \left(\cos\left( \frac{5\pi}{6} \right) +i\sin \left( \frac{5\pi}{6} \right) \right)= 2 \sqrt{3}\text{e}^{\text{i}\frac{5\pi}{6}}$$ La bonne réponse est c. Une forme exponentielle du nombre complexe $- 3 + \text{i}\sqrt{3}$ est $2 \sqrt{3}\text{e}^{\text{i}\frac{5\pi}{6}}$.
- On considère le nombre complexe $z = \dfrac{1}{2}\text{e}^{-\text{i}\frac{\pi}{4}}$. Le nombre $z^2$ est :
- un nombre réel
- un nombre complexe de partie réelle nulle
- un nombre complexe de module 1
- un nombre complexe de partie imaginaire positive
$$\begin{array}{rl} z^2&= \left ( = \dfrac{1}{2}\text{e}^{-\text{i}\frac{\pi}{4}} \right )\\ &= \dfrac{1}{4}\text{e}^{-\text{i}\frac{2\pi}{4}} \\ &= \dfrac{1}{4}\text{e}^{-\text{i}\frac{\pi}{2}} \\ &= \dfrac{1}{4} \left(\cos\left( \frac{ -\pi}{2} \right) +i\sin \left(-\frac{ \pi}{2} \right) \right) \\ &= \dfrac{1}{4}(0-i) \\ &=-\dfrac{1}{4}i \end{array}$$ La bonne réponse est donc b. $z^2$ est un nombre complexe de partie réelle nulle.
- Une variable aléatoire $T$ suit la loi uniforme sur un intervalle de la forme $[2~;~x]$, où $x$ est un réel strictement supérieur à 2. Sachant que $P(2 \leqslant T \leqslant 3) = \dfrac{1}{4}$, la valeur de $x$ est :
- 2,25
- 6
- 8
- 10
$$\begin{array}{ll}P(2 \leqslant T \leqslant 3) = \dfrac{1}{4}&\iff \dfrac{3-2}{x-2} = \dfrac{1}{4}\\ &\iff \dfrac{1}{x-2} = \dfrac{1}{4}\\ &\iff x-2 = 4 \\& \iff x=6 \end{array}$$Réponse b.
- Sur le graphique ci-dessous, la surface grisée est délimitée par la courbe d'équation $y = \dfrac{1}{x}$, l'axe des abscisses et les droites d'équation $x = \text{e}$ et $x = a$, où $a$ est un réel strictement supérieur à e.
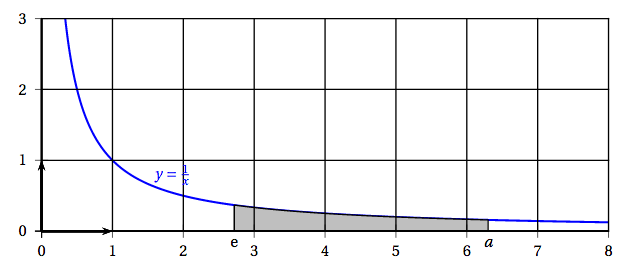
La surface grisée a une aire strictement comprise entre 1 et $1,5$ unité d'aire lorsque $a$ est égal à:
- 2e
- $2\text{e}^2$
- 3e
- $\text{e}^2$
La surface grisée a une aire $\mathcal A$ égale à $$\begin{array}{ll} \mathcal A&=\displaystyle\int_{\text{e}}^{a} \dfrac{1}{x} \text{d }x = \left [ \ln(x)\strut\right ]_{\text{e}}^{a}\\ &= \ln(a)-\ln(\text{e}) = \ln(a)-1 \end{array}$$ On veut $1< \mathcal{A} < 1,5$ donc $1 < \ln(a) -1 < 1,5$ ce qui équivaut à $2 < \ln(a) < 2,5$. La seule valeur de $a$ qui convienne est $a=3\text{e}$.
Réponse c.
Exercice 2
- Vues: 19226
