Baccalauréat S Asie 23 juin 2016 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

Un maraîcher est spécialisé dans la production de fraises. Cet exercice envisage dans la partie A la production de fraises, et dans la partie B leur conditionnement.
Les deux parties de cet exercice peuvent être traitées de façon indépendante.

Partie A: production de fraises

Le maraîcher produit ses fraises dans deux serres notées A et B ; 55% des fleurs de fraisier se trouvent dans la serre A, et 45% dans la serre B. Dans la serre A, la probabilité pour chaque fleur de donner un fruit est égale à 0,88 ; dans la serre B, elle est égale à 0,84.
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte.

• Proposition 1:
  La probabilité qu'une fleur de fraisier, choisie au hasard dans cette exploitation, donne un fruit est égale à 0,862.

On appelle :

• $A$ l’événement “la fleur de fraisier vient de la serre A”;
• $B$ l’événement “la fleur de fraisier vient de la serre B”;
• $F$ l’événement “la fleur donne un fruit”;




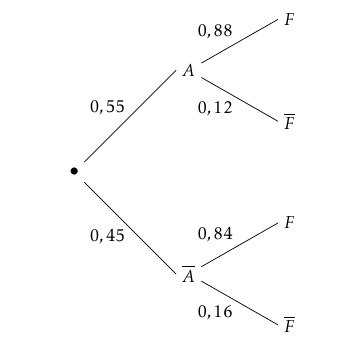
Proposition 1 : vraie

D’après la formule des probabilités totales on a :
$\begin{align*} p(F)&=p(A\cap F)+p(B \cap F) \\ &=0,55\times 0,88 + 0,45 \times 0,84 \\ &=0,862 \end{align*}$

$\quad$

• Proposition 2:
  On constate qu'une fleur, choisie au hasard dans cette exploitation, donne un fruit. La probabilité qu'elle soit située dans la serre A, arrondie au millième, est égale à 0,439.

Proposition 2 : fausse

On veut calculer :
$\begin{align*} p_F(A)&=\dfrac{p(A \cap F)}{p(F)} \\ &=\dfrac{0,55 \times 0,88}{0,862} \\ & \approx 0,561 \end{align*}$

$\quad$

Partie B: conditionnement des fraises

Les fraises sont conditionnées en barquettes. La masse (exprimée en gramme) d'une barquette peut être modélisée par une variable aléatoire $X$ qui suit la loi normale d'espérance $\mu=250$ et d'écart-type $\sigma$. La représentation graphique de la fonction densité de la loi de probabilité de la variable aléatoire $X$ est donnée ci-après: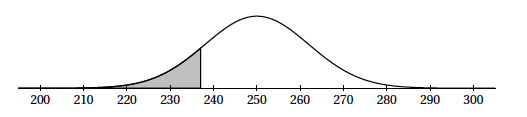

1. On donne $P(X \leqslant237)=0,14$. Calculer la probabilité de l'évènement « la masse de la barquette est comprise entre 237 et 263 grammes ».
$250-237 = 13$ et $250+13=263$. Donc $P(X \geqslant 263)=P(X \leqslant 237)=0,14$.
$\begin{align*} P(237 \leqslant X \leqslant 263)&=1-\left(P(X \leqslant 237)+P(X \geqslant 263)\right) \\ &= 1-0,28 \\ &=0,72 \end{align*}$
$\quad$
2. On note $Y$ la variable aléatoire définie par: $Y=\dfrac{X-250}{\sigma}$.
   1. Quelle est la loi de la variable aléatoire $Y$?
   La variable aléatoire $Y=\dfrac{X-250}{\sigma}$ suit la loi normale centrée réduite.
   $\quad$
   
   2. Démontrer que $P\left ( Y \leqslant- \dfrac{13}{\sigma}\right ) = 0,14$.
   $\begin{align*} P(X \leqslant 237) = 0,14 &\iff P\left(\dfrac{X-250}{\sigma} \leqslant \dfrac{237-250}{\sigma}\right) = 0,14 \\ &\iff \iff P\left(Y{\sigma} \leqslant -\dfrac{13}{\sigma}\right) = 0,14 \end{align*}$
   
   3. En déduire la valeur de $\sigma$ arrondie à l'entier.
   Donc, en utilisant la touche inverse loi normale de la calculatrice on trouve que :
   $-\dfrac{13}{\sigma} \approx -1,08$
   Par conséquent $\sigma \approx \dfrac{-1,08}{-13}$ soit $\sigma \approx 12$.
   $\quad$
3. Dans cette question, on admet que $\sigma$ vaut 12. On désigne par $n$ et $m$ deux nombres entiers.
   1. Une barquette est conforme si sa masse, exprimée en gramme, se trouve dans l'intervalle $\texttt{[} 250-n~;~250+n \texttt{]}$. Déterminer la plus petite valeur de $n$ pour qu'une barquette soit conforme, avec une probabilité supérieure ou égale à 95%.
   On veut trouver le plus petit entier naturel $n$ tel que :
   $\begin{align*} P(250-n \leqslant X \leqslant 250+n) \geqslant 0,95 &\iff P\left(\dfrac{-n}{12} \leqslant \dfrac{X-250}{12} \leqslant \dfrac{n}{12}\right) \geqslant 0,95 \\ &\iff 2P\left(\dfrac{X-250}{12} \leqslant \dfrac{n}{12}\right)-1\geqslant 0,95 \\ &\iff 2P\left(\dfrac{X-250}{12} \leqslant \dfrac{n}{12}\right) \geqslant 1,95 \\ &\iff P\left(\dfrac{X-250}{12} \leqslant \dfrac{n}{12}\right) \geqslant 0,975 \end{align*}$
   Puisque la variable aléatoire $\dfrac{X-250}{12}$ suit la loi normale centrée réduite on trouve donc, à l’aide de la calculatrice, $\dfrac{n}{12} \geqslant 1,960$ soit $n \geqslant 23,52$ et donc $n \geqslant 24$.
   Remarque : On pouvait remarquer qu’on nous demandait de trouver $u_{\alpha}$ tel que $P\left(-u_{\alpha} \leqslant X \leqslant u_{\alpha}\right) = 1-0,05$ et d’après le cours $u_{\alpha}\approx 1,96$.
   $\quad$
   
   2. On considère dans cette question qu'une barquette est conforme si sa masse, exprimée en gramme,se trouve dans l'intervalle $\texttt{[} 230~;~m\texttt{]}$. Déterminer la plus petite valeur de $m$ pour qu'une barquette soit conforme, avec une probabilité supérieure ou égale à 95%.
   On veut trouver la plus petite valeur de $m$ telle que :
   $\begin{align*} P(230 \leqslant X \leqslant m) \geqslant 0,95 &\iff 1-P(X \leqslant 230)-P(X \geqslant m) \geqslant 0,95\\ &\iff P(X \leqslant m)-P(X \leqslant 230) \geqslant 0,95 \\ &\iff P(X \leqslant m)-\left(0,5-P(230 \leqslant X \leqslant 250)\right)\geqslant 0,95 \\ &\iff P(X \leqslant m)-0,047~8\geqslant 0,95 \\ &\iff P(X \leqslant m) \geqslant 0,9978 \\ &\iff m\geqslant 284,18 \end{align*}$
   La plus petite valeur de $m$ cherchée est donc environ $285$