Baccalauréat S Antilles-Guyane 20 juin 2016 - Exercice 3
Page 5 sur 10
Exercice 3 è points
Partie A
On considère la fonction $f$ définie pour tout réel $x$ par $f(x)=x\text{e}^ {1-x^2}$.
- Calculer la limite de la fonction $f$ en $+\infty$.
Indication: on pourra utiliser que pour tout réel $x$ différent de $0$, $f(x)=\frac{\text{e}}{x}\times\frac{x^2}{\text{e}^ {x^2}}$.
On admettra que la limite de la fonction $f$ en $-\infty$ est égale à 0. -
- On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
Démontrer que pour tout réel $x$, \[ f'(x)=\left(1-2x^2\right)\text{e}^ {1-x^2}. \] - En déduire le tableau de variations de la fonction $f$.
- On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
Partie B
On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=\text{e}^ {1-x}$.
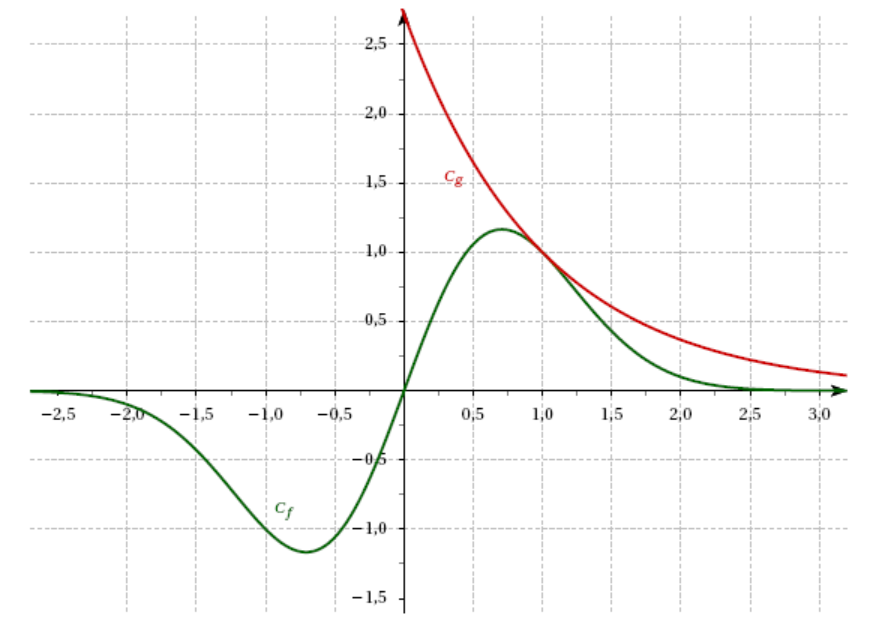
Sur le graphique ci-dessous, on a tracé dans un repère les courbes représentatives $\mathcal{C}_f$ et $\mathcal{C}_g$ respectivement des fonctions $f$ et $g$.
Le but de cette partie est d'étudier la position relative de ces deux courbes.
- Après observation du graphique, quelle conjecture peut-on émettre ?
- Justifier que, pour tout réel $x$ appartenant à $]-\infty~;~0]$, $f(x)<g(x)$.
- Dans cette question, on se place dans l'intervalle $]0~;~+\infty[$.
On pose, pour tout réel $x$ strictement positif, $\Phi(x)=\ln x-x^2+x$.- Montrer que, pour tout réel $x$ strictement positif, \[ f(x)\leqslant g(x)\text{ équivaut à }\Phi(x)\leqslant 0. \] On admet pour la suite que $f(x)=g(x)$ équivaut à $\Phi(x)=0$.
- On admet que la fonction $\Phi$ est dérivable sur $]0~;~+\infty[$. Dresser le tableau de variation de la fonction $\Phi$. (Les limites en $0$ et $+\infty$ ne sont pas attendues.)
- En déduire que, pour tout réel $x$ strictement positif, $\Phi(x)\leqslant 0$.
-
- La conjecture émise à la question 1. de la partie B est-elle valide ?
- Montrer que $\mathcal{C}_f$ et $\mathcal{C}_g$ ont un unique point commun, noté $A$.
- Montrer qu'en ce point $A$, ces deux courbes ont la même tangente.
Partie C
- Trouver une primitive $F$ de la fonction $f$ sur $\mathbb R$.
- En déduire la valeur de $\displaystyle\int_0^1\left(\text{e}^ {1-x}-x\text{e}^ {1-x^2}\right)\text{d}x$.
- Interpréter graphiquement ce résultat.
- Vues: 33964