Baccalauréat S Antilles-Guyane 20 juin 2016

 

Exercice 1 5 points

Commun à tous les candidats

Les valeurs approchées des résultats seront données à $10^{-4}$ près .
Les parties A et B sont indépendantes

Partie A

Un fabricant d'ampoules possède deux machines, notées A et B. La machine A fournit 65% de la production, et la machine B fournit le reste. Certaines ampoules présentent un défaut de fabrication:

• à la sortie de la machine A, 8% des ampoules présentent un défaut;
• à la sortie de la machine B, 5% des ampoules présentent un défaut.

On définit les événements suivants:

• $A$: « l'ampoule provient de la machine A»;
• $B$: « l'ampoule provient de la machine B»;
• $D$: « l'ampoule présente un défaut».

1. On prélève un ampoule au hasard parmi la production totale d'une journée.
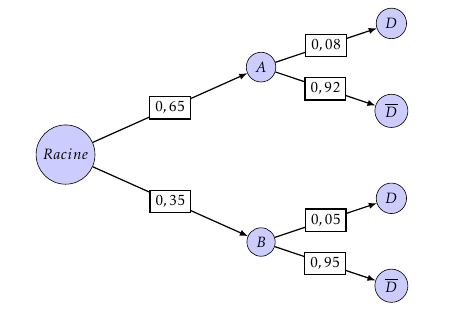
   1. Construire un arbre pondéré représentant la situation.
   2. Montrer que la probabilité de tirer une ampoule sans défaut est égale à 0,9305.
   3. L'ampoule tirée est sans défaut.
      Calculer la probabilité qu'elle provienne de la machine A.
2. On prélève 10 ampoules au hasard parmi la production d'une journée à la sortie de la machine A. La taille du stock permet de considérer les épreuves comme indépendantes et d'assimiler les tirages à tirages avec remise.
   Calculer la probabilité d'obtenir au moins 9 ampoules sans défaut.

Partie B

1. On rappelle que si $T$ suit une loi exponentielle de paramètre $\lambda$ ($\lambda$ étant un réel strictement positif) alors pour tout réel positif $a$, $\displaystyle P(T\leqslant a)=\int\limits_0^a\lambda\text{e}^ {-\lambda x}\text{d}x$.
   1. Montrer que $P(T\geqslant a)=\text{e}^ {-\lambda a}$.
   2. Montrer que si $T$ suit une loi exponentielle alors pour tous les réels positifs $t$ et $a$ on a \[ P_{T\geqslant t}(T\geqslant t+a)=P(T\geqslant a). \]
2. Dans cette partie, la durée de vie en heures d'une ampoule sans défaut est une variable aléatoire $T$ qui suit la loi exponentielle d'espérance 10000 .
   1. Déterminer la valeur exacte du paramètre $\lambda$ de cette loi.
   2. Calculer la probabilité $P(T\geqslant 5000 )$.
   3. Sachant qu'une ampoule sans défaut a déjà fonctionné pendant 7000 heures, calculer la probabilité que sa durée de vie totale dépasse 12000 heures.

Partie C

L'entreprise a cherché à améliorer la qualité de sa production et affirme qu'il n'y a pas plus de 6% d'ampoules défectueuses dans sa production. Une association de consommateurs réalise un test sur un échantillon et obtient 71 ampoules défectueuses sur 1000 .

1. Dans le cas où il y aurait exactement 6% d'ampoules défectueuses, déterminer un intervalle de fluctuation asymptotique au seuil de 95% de la fréquence d'ampoules défectueuses sur un échantillon aléatoire de taille 1000 .
2. A-t-on des raisons de remettre en cause l'affirmation de l'entreprise ?

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Les valeurs approchées des résultats seront données à $10^{-4}$ près .
Les parties A et B sont indépendantes

Partie A

Un fabricant d'ampoules possède deux machines, notées A et B. La machine A fournit 65% de la production, et la machine B fournit le reste. Certaines ampoules présentent un défaut de fabrication:

• à la sortie de la machine A, 8% des ampoules présentent un défaut;
• à la sortie de la machine B, 5% des ampoules présentent un défaut.

On définit les événements suivants:

• $A$: « l'ampoule provient de la machine A»;
• $B$: « l'ampoule provient de la machine B»;
• $D$: « l'ampoule présente un défaut».

1. On prélève un ampoule au hasard parmi la production totale d'une journée.
   1. Construire un arbre pondéré représentant la situation.
   
   
   2. Montrer que la probabilité de tirer une ampoule sans défaut est égale à 0,9305.
   D’après la formule des probabilités totales on a :
   $\begin{align*} p\left(\overline{D}\right) &=p\left(A \cap \overline{D}\right)+p\left(B \cap \overline{D}\right) \\
   &=0,65\times 0,92+0,35\times 0,95 \\
   &=0,930~5
   \end{align*}$
   $\quad$
   
   3. L'ampoule tirée est sans défaut.
      Calculer la probabilité qu'elle provienne de la machine A.
   On veut calculer :
   $\begin{align*} p_{\overline{D}}(A) &=\dfrac{p\left(A \cap \overline{D}\right)}{p\left(\overline{D}\right)} \\
   &=\dfrac{0,65 \times 0,92}{0,930~5} \\
   &=\dfrac{0,598}{0,930~5} \\
   &\approx 0,642~7
   \end{align*}$
   $\quad$
2. On prélève 10 ampoules au hasard parmi la production d'une journée à la sortie de la machine A. La taille du stock permet de considérer les épreuves comme indépendantes et d'assimiler les tirages à tirages avec remise.
   Calculer la probabilité d'obtenir au moins 9 ampoules sans défaut.
On appelle $X$ la variable aléatoire comptant le nombre d’ampoules sans défaut.
On effectue $10$ tirages aléatoires, indépendants, identiques et possédant chacun exactement deux issues : $D$ et $\overline{D}$. On sait que $\left(\overline{D}\right)=0,930~5$.
$n=10$ et $p=0,930~5$.
Par conséquent $X$ suit la loi binomiale de paramètres $n=10$ et $p=0,930~5$.
On veut calculer :
$\begin{align*} P(X\geqslant 9) &=P(X=9)+P(X = 10)
&\approx 0,85
\end{align*}$
$\quad$

Partie B

1. On rappelle que si $T$ suit une loi exponentielle de paramètre $\lambda$ ($\lambda$ étant un réel strictement positif) alors pour tout réel positif $a$, $\displaystyle P(T\leqslant a)=\int\limits_0^a\lambda\text{e}^ {-\lambda x}\text{d}x$.
   1. Montrer que $P(T\geqslant a)=\text{e}^ {-\lambda a}$.
   $\begin{align*} P(T \geqslant a) &= 1-P(X\leqslant a) \\
   &=\displaystyle 1-\int_0^a \lambda\text{e}^{-\lambda x}\mathrm{d}x \\
   &=1-\big[-\text{e}^{-\lambda x}\big]_0^a \\
   &=1+\text{e}^{-\lambda a}-1 \\
   &=\text{e}^{-\lambda a}
   \end{align*}$
   $\quad$
   
   2. Montrer que si $T$ suit une loi exponentielle alors pour tous les réels positifs $t$ et $a$ on a \[ P_{T\geqslant t}(T\geqslant t+a)=P(T\geqslant a). \]
   Soit $t$ et $a$ deux réels positifs.
   $\begin{align*} \displaystyle P_{T \geqslant t}\left(T \geqslant t+a\right) &=\dfrac{P\left(\left(T \geqslant t\right)\cap \left(T \geqslant t+a\right)\right)}{P\left(T\geqslant t\right)} \\
   &=\dfrac{P\left(T\geqslant t+a\right)}{P\left(T \geqslant t\right)} \\
   &=\dfrac{\text{e}^{-\lambda(t+a)}}{\text{e}^{-\lambda t}} \\
   &=\text{e}^{-\lambda a} \\
   &=P\left(T\geqslant a\right)
   \end{align*}$
   $\quad$
2. Dans cette partie, la durée de vie en heures d'une ampoule sans défaut est une variable aléatoire $T$ qui suit la loi exponentielle d'espérance 10000 .
   1. Déterminer la valeur exacte du paramètre $\lambda$ de cette loi.
   On sait que $E(T)=10~000$. Or $E(T)=\dfrac{1}{\lambda}$ donc $\lambda =\dfrac{1}{10~000} = 10^{-4}$
   $\quad$
   
   2. Calculer la probabilité $P(T\geqslant 5000 )$.
   $P(T\geqslant 5~000)=\text{e}^{-5~000\times 10^{-4}}\approx 0,606~5$
   $\quad$
   
   3. Sachant qu'une ampoule sans défaut a déjà fonctionné pendant 7000 heures, calculer la probabilité que sa durée de vie totale dépasse 12000 heures.
   On veut calculer
   $\begin{align*} P_{T \geqslant 7~000}(T \geqslant 12~000) &= P_{T \geqslant 7~000}(T \geqslant 7~000+5~000) \\
   &= P(T \geqslant 5~000) \\
   &\approx 0,606~5
   \end{align*}$
   $\quad$

Partie C

L'entreprise a cherché à améliorer la qualité de sa production et affirme qu'il n'y a pas plus de 6% d'ampoules défectueuses dans sa production. Une association de consommateurs réalise un test sur un échantillon et obtient 71 ampoules défectueuses sur 1000 .

1. Dans le cas où il y aurait exactement 6% d'ampoules défectueuses, déterminer un intervalle de fluctuation asymptotique au seuil de 95% de la fréquence d'ampoules défectueuses sur un échantillon aléatoire de taille 1000 .
On a $n=1~000 \geqslant 30$ et $p=0,06$ donc $np=60 \geqslant 5$ et $n(1-p)=940 \geqslant 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$\begin{align*} I_{1~000} &=\left[0,06-1,96\times \sqrt{\dfrac{0,06\times 0,94}{1~000}};0,06+1,96\times \sqrt{\dfrac{0,06\times 0,94}{1~000}} \right] \\
&\approx [0,045~2;0,074~8]
\end{align*}$
$\quad$
2. A-t-on des raisons de remettre en cause l'affirmation de l'entreprise ?
La fréquence observée est $f=\dfrac{71}{1~000}=0,071\in I_{1~000}$
Au risque d’erreur de $5\%$ on ne peut pas remettre en cause l’affirmation de l’entreprise.
$\quad$

Exercice 2  3 points

Commun à tous les candidats

On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On note $\mathcal{C}$ l'ensemble des points $M$ du plan d'affixe $z$ tels que $\left\vert z-2\right\vert=1$.

1. Justifier que $\mathcal{C}$ est un cercle, dont on précisera le centre et le rayon.
2. Soit $a$ un nombre réel. On appelle $\mathcal{D}$ la droite d'équation $y=ax$.
   Déterminer le nombre de points d'intersection entre $\mathcal{C}$ et $\mathcal{D}$ en fonction des valeurs du réel $a$.

Correction de l'exercice 2 (3 points)

Commun à tous les candidats

On munit le plan complexe d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On note $\mathcal{C}$ l'ensemble des points $M$ du plan d'affixe $z$ tels que $\left\vert z-2\right\vert=1$.

1. Justifier que $\mathcal{C}$ est un cercle, dont on précisera le centre et le rayon.
On appelle $M$ le point d’affixe $z$ et $A$ le point d’affixe $2$.
$|z-2|=1 \iff AM=1$
Donc $\mathscr{C}$ est le cercle de centre $A$ et de rayon $1$.
$\quad$
2. Soit $a$ un nombre réel. On appelle $\mathcal{D}$ la droite d'équation $y=ax$.
   Déterminer le nombre de points d'intersection entre $\mathcal{C}$ et $\mathcal{D}$ en fonction des valeurs du réel $a$.
Si un point $M$ appartient à la droite $\mathscr{D}$ alors ses coordonnées sont $(x;ax)$ et donc son affixe est $z=x+ax\text{i}$.
Ainsi :
$\begin{align*} |x+ax \text{i} -2|=1 &\iff \left|(x-2)+ax \text{i}\right| = 1 \\
&\iff (x-2)^2+(ax)^2 = 1 \\
&\iff x^2-4x+4+a^2x^2=1\\
&\iff \left(a^2+1\right)x^2-4x+3=0
\end{align*}$
Le discriminant est :
$\begin{align*} \Delta &=16-12\left(1+a^2\right) \\
&=4\left(4-3-3a^2\right) \\
&=4\left(1-3a^2\right)
\end{align*}$
Or $1-3a^2=0 \iff a^2=\dfrac{1}{3} \iff a=-\dfrac{\sqrt{3}}{3}$ ou $a=\dfrac{\sqrt{3}}{3}$.
Par conséquent :
• si $a\in \left]-\dfrac{\sqrt{3}}{3};\dfrac{\sqrt{3}}{3}\right[$ alors $\Delta >0$ et le cercle et la droite ont deux points en commun;
• si $a=-\dfrac{\sqrt{3}}{3}$ ou si $a=\dfrac{\sqrt{3}}{3}$ alors $\Delta =0$ et la droite et le cercle n’ont qu’un point en commun;
• si $x\in \left]-\infty;-\dfrac{\sqrt{3}}{3}\right[\cup\left]\dfrac{\sqrt{3}}{3};+\infty\right[$ alors $\Delta <0$ et la droite et le cercle n’ont aucun point en commun.

 

Une animation ?

 

 

Exercice 3 è points

Fonctions

Partie A

On considère la fonction $f$ définie pour tout réel $x$ par $f(x)=x\text{e}^ {1-x^2}$.

1. Calculer la limite de la fonction $f$ en $+\infty$.
   Indication: on pourra utiliser que pour tout réel $x$ différent de $0$, $f(x)=\frac{\text{e}}{x}\times\frac{x^2}{\text{e}^ {x^2}}$.
   On admettra que la limite de la fonction $f$ en $-\infty$ est égale à 0.
2. 1. On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
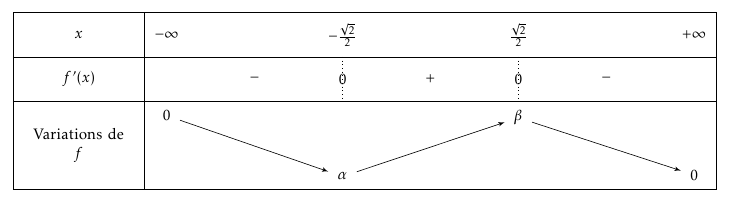
      Démontrer que pour tout réel $x$, \[ f'(x)=\left(1-2x^2\right)\text{e}^ {1-x^2}. \]
   2. En déduire le tableau de variations de la fonction $f$.

Partie B

On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=\text{e}^ {1-x}$.
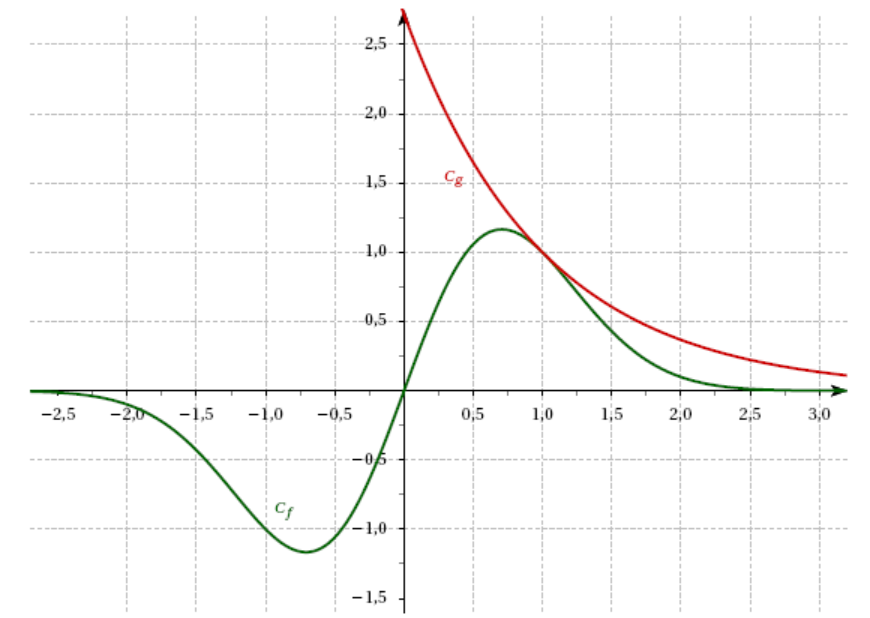
Sur le graphique ci-dessous, on a tracé dans un repère les courbes représentatives $\mathcal{C}_f$ et $\mathcal{C}_g$ respectivement des fonctions $f$ et $g$.

Le but de cette partie est d'étudier la position relative de ces deux courbes.

1. Après observation du graphique, quelle conjecture peut-on émettre ?
2. Justifier que, pour tout réel $x$ appartenant à $]-\infty~;~0]$, $f(x)<g(x)$.
3. Dans cette question, on se place dans l'intervalle $]0~;~+\infty[$.
   On pose, pour tout réel $x$ strictement positif, $\Phi(x)=\ln x-x^2+x$.
   1. Montrer que, pour tout réel $x$ strictement positif, \[ f(x)\leqslant g(x)\text{ équivaut à }\Phi(x)\leqslant 0. \] On admet pour la suite que $f(x)=g(x)$ équivaut à $\Phi(x)=0$.
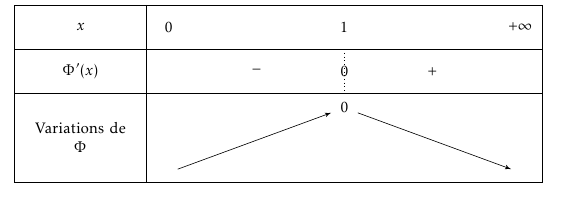
   2. On admet que la fonction $\Phi$ est dérivable sur $]0~;~+\infty[$. Dresser le tableau de variation de la fonction $\Phi$. (Les limites en $0$ et $+\infty$ ne sont pas attendues.)
   3. En déduire que, pour tout réel $x$ strictement positif, $\Phi(x)\leqslant 0$.
4. 1. La conjecture émise à la question 1. de la partie B est-elle valide ?
   2. Montrer que $\mathcal{C}_f$ et $\mathcal{C}_g$ ont un unique point commun, noté $A$.
   3. Montrer qu'en ce point $A$, ces deux courbes ont la même tangente.

Partie C

1. Trouver une primitive $F$ de la fonction $f$ sur $\mathbb R$.
2. En déduire la valeur de $\displaystyle\int_0^1\left(\text{e}^ {1-x}-x\text{e}^ {1-x^2}\right)\text{d}x$.
3. Interpréter graphiquement ce résultat.

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Partie A

On considère la fonction $f$ définie pour tout réel $x$ par $f(x)=x\text{e}^ {1-x^2}$.

1. Calculer la limite de la fonction $f$ en $+\infty$.
   Indication: on pourra utiliser que pour tout réel $x$ différent de $0$, $f(x)=\frac{\text{e}}{x}\times\frac{x^2}{\text{e}^ {x^2}}$.
   On admettra que la limite de la fonction $f$ en $-\infty$ est égale à 0.
2. $f(x)=x\text{e}^{1-x^2}=x\text{e}\times \dfrac{1}{\text{e}^{x^2}}=\dfrac{\text{e}}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$
   $\lim\limits_{x \to +\infty} x^2=+\infty$ et $\lim\limits_{X \to +\infty} \dfrac{\text{e}^X}{X}=+\infty$ par conséquent $\lim\limits_{X \to +\infty} \dfrac{X}{\text{e}^X}=0$
   Donc $\lim\limits_{x \to +\infty} \dfrac{x^2}{\text{e}^{x^2}}=0$.
   De plus $\lim\limits_{x \to +\infty} \dfrac{\text{e}}{x}=0$.
   Donc $\lim\limits_{x \to +\infty} f(x)=0$
   $\quad$
   1. On admet que $f$ est dérivable sur $\mathbb R$ et on note $f'$ sa dérivée.
      Démontrer que pour tout réel $x$, \[ f'(x)=\left(1-2x^2\right)\text{e}^ {1-x^2}. \]
   $\begin{align*} f'(x)&=\text{e}^{1-x^2}+x\times (-2x)\text{e}^{1-x^2} \\
   &=\left(1-2x^2\right)\text{e}^{1-x^2}
   \end{align*}$
   $\quad$
   
   2. En déduire le tableau de variations de la fonction $f$.
   La fonction exponentielle est strictement positive. Le signe de $f'(x)$ ne dépend donc que de celui de $1-2x^2$.
   $1-2 x^2 $ est un trinôme du second degré qui a pour racines $-\frac{\sqrt 2}{2}$ et $\frac{\sqrt 2}{2}$; il a donc le signe de $a=-2$ à l'extérieur des racines et celui de $-a$ à l'intérieur.et $1-2x^2>0 \iff \dfrac{1}{2}>x^2 \iff x \in \left[-\dfrac{\sqrt{2}}{2};\dfrac{\sqrt{2}}{2}\right]$
   On obtient ainsi le tableau de variations suivant :
   
   où $\alpha=f\left(-\dfrac{\sqrt{2}}{2}\right)=-\dfrac{\sqrt{2}}{2}\text{e}^{0,5}$ et $\beta =f\left(-\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2}\text{e}^{0,5}$

Partie B

On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=\text{e}^ {1-x}$.
Sur le graphique ci-dessous, on a tracé dans un repère les courbes représentatives $\mathcal{C}_f$ et $\mathcal{C}_g$ respectivement des fonctions $f$ et $g$.

Le but de cette partie est d'étudier la position relative de ces deux courbes.

1. Après observation du graphique, quelle conjecture peut-on émettre ?
Il semblerait que $\mathscr{C}_g$ soit toujours au-dessus de $\mathscr{C}_f$.
$\quad$
2. Justifier que, pour tout réel $x$ appartenant à $]-\infty~;~0]$, $f(x)<g(x)$.
Pour tout $x\in]-\infty;0]$, $f(x) \leqslant 0$ et $g(x)>0$.
Donc sur cet intervalle $f(x)< g(x)$.
$\quad$
3. Dans cette question, on se place dans l'intervalle $]0~;~+\infty[$.
   On pose, pour tout réel $x$ strictement positif, $\Phi(x)=\ln x-x^2+x$.
   1. Montrer que, pour tout réel $x$ strictement positif, \[ f(x)\leqslant g(x)\text{ équivaut à }\Phi(x)\leqslant 0. \] On admet pour la suite que $f(x)=g(x)$ équivaut à $\Phi(x)=0$.
   Pour tout $x\in]-\infty;0]$, $f(x) \leqslant 0$ et $g(x)>0$.
   Donc sur cet intervalle $f(x)< g(x)$.
   $\quad$
   2. On admet que la fonction $\Phi$ est dérivable sur $]0~;~+\infty[$. Dresser le tableau de variation de la fonction $\Phi$. (Les limites en $0$ et $+\infty$ ne sont pas attendues.)
   
   $\begin{align*} f(x) \leqslant g(x) &\iff x\text{e}^{1-x^2}\leqslant \text{e}^{1-x} \\
   &\iff x \leqslant \dfrac{\text{e}^{1-x}}{\text{e}^{1-x^2}} \\
   &\iff x \leqslant \text{e}^{x^2-x} \\
   &\iff \ln x \leqslant x^2-x \\
   &\iff \Phi(x) \leqslant 0
   \end{align*}$
   $\quad$
   b. $\Phi'(x)=\dfrac{1}{x}-2x+1 = \dfrac{-2x^2+x+1}{x}$
   Pour tout $x\in ]0;+\infty[$, le signe de $\Phi'(x)$ ne dépend que de celui de $-2x^2+x+1$
   $\Delta = 1^2-4\times (-2)=9 >0$
   $-2 x^2+x+1$ est un trinôme du second degré qui a pour racines $-\frac{1}{2}$ et $1$; il a donc le signe de $a=-2$ à l'extérieur des racines et celui de $-a$ à l'intérieur.
   
   On obtient donc le tableau de variations suivant :
   
   
   3. En déduire que, pour tout réel $x$ strictement positif, $\Phi(x)\leqslant 0$.
   D’après le tableau de variations, pour tout réel $x >0$ on a $\Phi(x) \leqslant 0$.En effet $\Phi$ présente un maximum en $1$ qui vaut $0$
   
   $\quad$
4. 1. La conjecture émise à la question 1. de la partie B est-elle valide ?
   D’après la question 3.a. pour tout réel $x$ strictement positif, $f(x) \leqslant g(x) \iff \Phi(x) \leqslant 0$.
   Ainsi, $\mathscr{C}_f$ est bien toujours en dessous de $\mathscr{C}_g$ sur $]0;+\infty[$.
   On a prouvé que pour tout $x \leqslant 0$, $f(x)\leqslant g(x)$.
   Donc $\mathscr{C}_f$ est bien toujours en dessous de $\mathscr{C}_g$ sur $]-\infty;0]$.
   La conjecture de la question 1. est donc valide.
   $\quad$
   
   2. Montrer que $\mathcal{C}_f$ et $\mathcal{C}_g$ ont un unique point commun, noté $A$.
   Sur $]-\infty;0]$, $f(x) < g(x)$ : les deux courbes n’ont pas de point commun sur cet intervalle.
   Sur $]0;+\infty[$, $f(x)=g(x) \iff \Phi(x)=0 \iff x=1$
   $\mathscr{C}_g$ et $\mathscr{C}_f$ ont donc un unique point commun : le point $A$ d’abscisse $1$.
   $g(1)=\text{e}^0=1$.
   $\quad$
   
   3. Montrer qu'en ce point $A$, ces deux courbes ont la même tangente.
   $f'(1)=(1-2)\text{e}^0=-1$ et $g'(1)=-\text{e}^0=-1$
   Les deux tangentes en $A$ ont donc le même coefficient directeur. Puisqu’elles passent par le point $A$ cela signifie donc qu’elles sont confondues.
   $\quad$

Partie C

1. Trouver une primitive $F$ de la fonction $f$ sur $\mathbb R$.
Une primitive de $f$ sur $\mathbb R$ est la fonction $F$ définie sur $\mathbb R$ par $F(x)=-\dfrac{1}{2}\text{e}^{1-x^2}$
$\quad$
2. En déduire la valeur de $\displaystyle\int_0^1\left(\text{e}^ {1-x}-x\text{e}^ {1-x^2}\right)\text{d}x$.
$\begin{align*} \displaystyle \int_0^1\left(\text{e}^{1-x}-x\text{e}^{1-x^2}\right)\mathrm{d}x &= \big[-\text{e}^{1-x}-F(x)\big]_0^1 \\
&=-1+\dfrac{1}{2}-\left(-\text{e}+\dfrac{1}{2}\text{e}\right) \\
&=\dfrac{1}{2}\left(\text{e}-1\right)
\end{align*}$
$\quad$
3. Interpréter graphiquement ce résultat.
Ce résultat correspond à l’aire du domaine compris entre $\mathscr{C}_g$, $\mathscr{C}_f$ et les droites d’équation $x=0$ et $x=1$.
$\quad$

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

$ABCDEFGH$ est un cube d'arête égale à 1.
L'espace est muni du repère orthonormé $(D~;\vec{DC},\vec{DA},\vec{DH})$.
Dans ce repère, on a:
$D(0~;~0~;~0)$, $C(1~;~0~;~0)$, $A(0~;~1~;~0)$,
$H(0~;~0~;~1)$ et $E(0~;~1~;~1)$.
Soit $I$ le milieu de $[AB]$.
 
Soit $\mathcal{P}$ le plan parallèle au plan $(BGE)$ et passant par le point $I$.
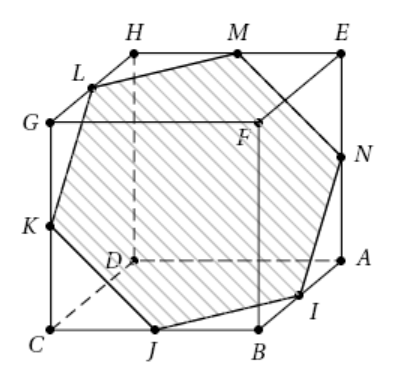
On admet que la section du cube par le plan $\mathcal{P}$ représentée ci-dessus est un hexagone dont les sommets $I$, $J$, $K$, $L$, $M$, et $N$ appartiennent respectivement aux arêtes $[AB]$, $[BC]$, $[CG]$, $[GH]$, $[HE]$ et $[AE]$.

1. 1. Montrer que le vecteur $\vec{DF}$ est normal au plan $(BGE)$.
   2. En déduire une équation cartésienne du plan $\mathcal{P}$.
2. Montrer que le point $N$ est le milieu du segment $[AE]$.
3. 1. Déterminer une représentation paramétrique de la droite $(HB)$.
   2. En déduire que la droite $(HB)$ et le plan $\mathcal{P}$ son sécants en un point $T$ dont on précisera les coordonnées.
4. Calculer, en unités de volume, le volume du tétraèdre $FBGE$.

 

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

$ABCDEFGH$ est un cube d'arête égale à 1.
L'espace est muni du repère orthonormé $(D~;\vec{DC},\vec{DA},\vec{DH})$.
Dans ce repère, on a:
$D(0~;~0~;~0)$, $C(1~;~0~;~0)$, $A(0~;~1~;~0)$,
$H(0~;~0~;~1)$ et $E(0~;~1~;~1)$.
Soit $I$ le milieu de $[AB]$.
 
Soit $\mathcal{P}$ le plan parallèle au plan $(BGE)$ et passant par le point $I$.
On admet que la section du cube par le plan $\mathcal{P}$ représentée ci-dessus est un hexagone dont les sommets $I$, $J$, $K$, $L$, $M$, et $N$ appartiennent respectivement aux arêtes $[AB]$, $[BC]$, $[CG]$, $[GH]$, $[HE]$ et $[AE]$.

1. 1. Montrer que le vecteur $\vec{DF}$ est normal au plan $(BGE)$.
   $\vec{DF}(1;1;1)$
   $\vec{BG}(0;-1;1)$ et $\vec{BE}(-1;0;1)$ ne sont clairement pas colinéaires.
   $\vec{DF}.\vec{BG}=0-1+1=0$ et $\vec{DF}.\vec{BE}=-1+0+1=0$
   Ainsi le vecteur $\vec{DF}$ est orthogonal à deux vecteurs non colinéaires du plan $(BGE)$.
   Il est par conséquent normal au plan $(BGE)$.
   $\quad$
   
   2. En déduire une équation cartésienne du plan $\mathcal{P}$.
   Le plan $\mathscr{P}$ est parallèle au plan $(BGE)$.
   $\vec{DF}$ est donc également normal à $(BGE)$.
   Une équation cartésienne de $\mathscr{P}$ est de la forme $$x+y+z+d=0$$
   Le point $I(0,5;1;0)$ appartient à ce plan donc :
   $$0,5+1+d=0 \iff d=-1,5$$
   Une équation cartésienne de $\mathscr{P}$ est donc $x+y+z-1,5=0$.
   $\quad$
2. Montrer que le point $N$ est le milieu du segment $[AE]$.
Le point $N$ appartient à $[AE]$. Ses coordonnées sont donc $\left(0;1;z_N\right)$.
Il appartient au plan $\mathscr{P}$ donc $0+1+z_N-1,5=0 \iff z_N=0,5$
Ainsi $N$ est le milieu de $[AE]$.
$\quad$
3. 1. Déterminer une représentation paramétrique de la droite $(HB)$.
   On a $\vec{HB}(-1;-1;1)$
   Une représentation paramétrique de la droite $(HB)$ est donc $\begin{cases} x=-t\\y=-t \quad t\in \mathbb R \\z=1+t \end{cases}$.
   
   2. En déduire que la droite $(HB)$ et le plan $\mathcal{P}$ son sécants en un point $T$ dont on précisera les coordonnées.
   $\vec{HB}.\vec{DF}=-1-1+1=-1 \neq 0$
   Le plan $\mathscr{P}$ et la droite $(HB)$ sont donc sécants.
   On injecte les équations de $(HB)$ dans l’équation de $\mathscr{P}$.
   $-t-t+1+t-1,5=0 \iff -t-0,5=0 \iff t=-0,5$
   Donc $T(0,5;0,5;0,5)$.
   $\quad$
4. Calculer, en unités de volume, le volume du tétraèdre $FBGE$.
Calculons dans un premier temps l’aire du triangle $BGF$ rectangle en $F$.
$\mathscr{A}=\dfrac{1\times 1}{2}=\dfrac{1}{2}$
Donc le volume du tétraèdre $FBGE$ est $\mathscr{V}=\dfrac{\dfrac{1}{2} \times 1}{3}=\dfrac{1}{6}$

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Les parties A et B sont indépendantes

Partie A

On considère l'équation suivante d'inconnues $x$ et $y$ entiers relatifs: \[ \text{(E)}\; 7x-3y=1. \]

1. Un algorithme incomplet est donné ci-dessous. Le recopier et le compléter, en écrivant ses lignes manquantes (1) et (2) de manière à ce qu'il donne les solutions entières $(x~;~y)$ de l'équation (E) vérifiant $-5\leqslant x\leqslant 10$ et $-5\leqslant y\leqslant 10$. $$\begin{array}{|l |l |}\hline \text{Variables:} & X \text{ est un nombre entier}\\ & Y \text{ est un nombre entier }\\ \text{Début: }& \text{ Pour } X \text{ variant de } -5 \text{ à } 10\\ &\phantom{XXXX} (1) \ldots\ldots\ldots\ldots\ldots \\ &\phantom{XXXXXXXX} (2) \ldots\ldots\ldots\ldots\ldots \\ &\phantom{XXXXXXXX} \text{Alors Afficher } X \text{ et } Y\\ &\phantom{XXXXXXXX} \text{ Fin Si }\\ &\phantom{XXXX}\text{ Fin Pour }\\ & \text{ Fin Pour }\\ \text{ Fin }& \hline \end{array}$$
2. 1. Donner une solution particulière de l'équation (E).
   2. Déterminer l'ensemble des couples d'entiers relatifs solutions de l'équation (E).
   3. Déterminer l'ensemble des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation (E) tels que $-5\leqslant x\leqslant 10$ et $-5\leqslant y\leqslant 10$.

Partie B

Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$.
On considère la droite $\mathcal{D}$ d'équation \[ 7x - 3y-1=0 \] On définie la suite $(A_n)$ de points du plan de coordonnées $(x_n~:~y_n)$ vérifiant pour tout $n$ entier naturel: \[ \left\{ \begin{array}{rcl} x_0&=&1\\ y_0&=&2 \end{array} \right.\qquad\text{et}\qquad \left\{ \begin{array}{rcl} x_{n+1}&=& - \frac{13}{2}x_n + 3y_n\\[1.5ex] y_{n+1}&=& - \frac{35}{2}x_n + 8y_n \end{array} \right. \]

1. On note $M$ la matrice $\begin{pmatrix} \frac{-13}{2}&3\\\frac{-35}{2}&8 \end{pmatrix}$ . Pour tout entier naturel $n$, on pose $X_n=\begin{pmatrix} x_n\\y_n \end{pmatrix}$.
   1. Montrer que, pour tout entier naturel $n$, $X_{n+1}=MX_n$.
   2. Sans justifier, exprimer pour tout entier naturel $n$, $X_n$ en fonction de $M^n$ et $X_0$.
2. On considère la matrice $P=\begin{pmatrix} -2&-3\\-5&-7 \end{pmatrix}$ et on admet que la matrice inverse de $P$, notée $P^{-1}$, est définie par $P^{-1}=\begin{pmatrix} 7&-3\\-5&2 \end{pmatrix}$.
   1. Vérifier que $P^{-1}MP$ est une matrice diagonale $D$ que l'on précisera.
   2. Pour tout entier naturel $n$, donner $D^n$ sans justification.
   3. Démontrer par récurrence que, pour tout entier naturel $n$, $M^n = PD^nP^{-1}$.
3. On admet que, pour tout entier naturel $n$, $M^n=\begin{pmatrix} -14+\frac{15}{2^n}&6-\frac{6}{2^n}\\[1.5ex] -35+\frac{35}{2^n}&15-\frac{14}{2^n} \end{pmatrix}$.
   En déduire que, pour tout entier naturel $n$, une expression de $x_n$ et $y_n$ en fonction de $n$.
4. Montrer que, pour tout entier naturel $n$, le point $A_n$ appartient à la droite $\mathcal{D}$.

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Les parties A et B sont indépendantes

Partie A

On considère l'équation suivante d'inconnues $x$ et $y$ entiers relatifs: \[ \text{(E)}\; 7x-3y=1. \]

1. Un algorithme incomplet est donné ci-dessous. Le recopier et le compléter, en écrivant ses lignes manquantes (1) et (2) de manière à ce qu'il donne les solutions entières $(x~;~y)$ de l'équation (E) vérifiant $-5\leqslant x\leqslant 10$ et $-5\leqslant y\leqslant 10$. $$\begin{array}{|l |l |}\hline \text{Variables:} & X \text{ est un nombre entier}\\ & Y \text{ est un nombre entier }\\ \text{Début: }& \text{ Pour } X \text{ variant de } -5 \text{ à } 10\\ &\phantom{XXXX} (1) \ldots\ldots\ldots\ldots\ldots \\ &\phantom{XXXXXXXX} (2) \ldots\ldots\ldots\ldots\ldots \\ &\phantom{XXXXXXXX} \text{Alors Afficher } X \text{ et } Y\\ &\phantom{XXXXXXXX} \text{ Fin Si }\\ &\phantom{XXXX}\text{ Fin Pour }\\ & \text{ Fin Pour }\\ \text{ Fin }& \hline \end{array}$$
Variables :
$\quad$ $X$ est un nombre entier
$\quad$ $Y$ est un nombre entier
Début :
$\quad$ Pour $X$ vairant de $-5$ à $10$
$\qquad$ Pour $Y$ variant de $-5$ à $10$
$\quad \qquad $ Si $7X-3Y=1$
$\quad \qquad$ Alors Afficher $X$ et $Y$
$\quad \qquad$ Fin Si
$\qquad$ Fin Pour
$\quad$ Fin Pour
Fin
$\quad$
2. 1. Donner une solution particulière de l'équation (E).
   $7\times 1 -3\times 2 = 7 -6 =1$
   Le couple $(1;2)$ est donc une solution particulière de $(E)$.
   $\quad$
   
   2. Déterminer l'ensemble des couples d'entiers relatifs solutions de l'équation (E).
   On considère une autre solution $(x;y)$ de $(E)$.
   On a donc $7x-3y=1$ et $7 \times 1 -3\times 2 = 1$
   Par différence on obtient $7(x-1)-3(y-2)=0$
   Soit $7(x-1)=3(y-2)$
   $7$ et $3$ sont premiers entre eux.
   D’après le théorème de Gauss, il existe donc un entier relatif $k$ tel que $x-1=3k$ et $y-2=7k$
   Soit $x=1+3k$ et $y=2+7k$.
   $\quad$
   Réciproquement: soit $k$ un entier relatif alors
   $7(1+3k)-3(2+7k)=7+21k-6-21k=1$
   $\quad$
   Les solutions de l’équation $(E)$ sont donc les couples $(1+3k;2+7k)$ pour tout entier relatif $k$.
   $\quad$
   
   3. Déterminer l'ensemble des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation (E) tels que $-5\leqslant x\leqslant 10$ et $-5\leqslant y\leqslant 10$.
   On veut que $-5 \leqslant 1+3k \leqslant 10$ et $-5 \leqslant 2+7k \leqslant 10$
   Soit $-6 \leqslant 3k \leqslant 9$ et $-7 \leqslant 7k \leqslant 8$
   D’où $ -2 \leqslant k \leqslant 3$ et $-1 \leqslant k \leqslant \dfrac{8}{7}$
   Les valeurs possibles pour $k$ sont donc $-1,0$ et $1$.
   Les couples recherchés sont donc $(-2;-5)$, $(1;2)$ et $(4;9)$.
   $\quad$

Partie B

Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$.
On considère la droite $\mathcal{D}$ d'équation \[ 7x - 3y-1=0 \] On définie la suite $(A_n)$ de points du plan de coordonnées $(x_n~:~y_n)$ vérifiant pour tout $n$ entier naturel: \[ \left\{ \begin{array}{rcl} x_0&=&1\\ y_0&=&2 \end{array} \right.\qquad\text{et}\qquad \left\{ \begin{array}{rcl} x_{n+1}&=& - \frac{13}{2}x_n + 3y_n\\[1.5ex] y_{n+1}&=& - \frac{35}{2}x_n + 8y_n \end{array} \right. \]

1. On note $M$ la matrice $\begin{pmatrix} \frac{-13}{2}&3\\\frac{-35}{2}&8 \end{pmatrix}$ . Pour tout entier naturel $n$, on pose $X_n=\begin{pmatrix} x_n\\y_n \end{pmatrix}$.
   1. Montrer que, pour tout entier naturel $n$, $X_{n+1}=MX_n$.
   $MX_n=\begin{pmatrix} -\dfrac{13}{2}x_n+3y_n \\-\dfrac{35}{2}x_n+8y_n \end{pmatrix}=X_{n+1}$
   $\quad$
   
   2. Sans justifier, exprimer pour tout entier naturel $n$, $X_n$ en fonction de $M^n$ et $X_0$.
   Pour tout entier naturel $n$ on a $X_n=M^nX_0$.
   $\quad$
2. On considère la matrice $P=\begin{pmatrix} -2&-3\\-5&-7 \end{pmatrix}$ et on admet que la matrice inverse de $P$, notée $P^{-1}$, est définie par $P^{-1}=\begin{pmatrix} 7&-3\\-5&2 \end{pmatrix}$.
   1. Vérifier que $P^{-1}MP$ est une matrice diagonale $D$ que l'on précisera.
   $P^{-1}MP=\begin{pmatrix}1&0\\0&\dfrac{1}{2}\end{pmatrix}$.
   On a donc $D=\begin{pmatrix}1&0\\0&\dfrac{1}{2}\end{pmatrix}$ qui est bien une matrice diagonale.
   $\quad$
   
   2. Pour tout entier naturel $n$, donner $D^n$ sans justification.
   Pour tout entier naturel $n$, on a : $D^n=\begin{pmatrix}1&0\\0&\dfrac{1}{2^n}\end{pmatrix}$.
   $\quad$
   
   3. Démontrer par récurrence que, pour tout entier naturel $n$, $M^n = PD^nP^{-1}$.
   Initialisation : Si $n=0$ alors $M^0=I_2$ où $I_2$ est la matrice identité.
   $PD^0P^{-1}=PI_2P^{-1}=PP^{-1}=I_2=M^0$
   La propriété est donc vraie au rang $0$.
   $\quad$
   Hérédité : On suppose la propriété vraie au rang $n$: $M^n=PD^nP^{-1}$
   $\begin{align*} M^{n+1}&= M^n \times M \\
   &=PD^nP^{-1}\times PDP^{-1} \\
   &=PD^nDP^{-1} \\
   &=PD^{n+1}P^{-1}
   \end{align*}$
   La propriété est donc vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$, on a $M^n=PD^nP^{-1}$.
   $\quad$
3. On admet que, pour tout entier naturel $n$, $M^n=\begin{pmatrix} -14+\frac{15}{2^n}&6-\frac{6}{2^n}\\[1.5ex] -35+\frac{35}{2^n}&15-\frac{14}{2^n} \end{pmatrix}$.
   En déduire que, pour tout entier naturel $n$, une expression de $x_n$ et $y_n$ en fonction de $n$.
On a $X_n=M^nX_0$
Donc $\begin{cases} x_n=-14+\dfrac{15}{2^n}+12-\dfrac{12}{2^n} \\y_n=-35+\dfrac{35}{2^n}+30-\dfrac{28}{2^n} \end{cases}$ soit $\begin{cases} x_n=-2+\dfrac{3}{2^n}\\y_n=-5+\dfrac{7}{2^n}\end{cases}$.
$\quad$
4. Montrer que, pour tout entier naturel $n$, le point $A_n$ appartient à la droite $\mathcal{D}$.
On considère un entier naturel $n$.
$\begin{align*} 7x_n-3y_n-1 &=-14+\dfrac{21}{2^n}+15-\dfrac{21}{2^n}-1 \\
&=1-1 \\
&=0
\end{align*}$
Pour tout entier naturel $n$, le point $A_n$ appartient bien à la droite $\mathscr{D}$.