Baccalauréat S Antilles-Guyane 20 juin 2016 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Les valeurs approchées des résultats seront données à $10^{-4}$ près .
Les parties A et B sont indépendantes

Partie A

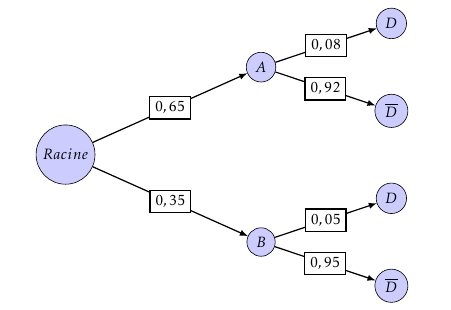
Un fabricant d'ampoules possède deux machines, notées A et B. La machine A fournit 65% de la production, et la machine B fournit le reste. Certaines ampoules présentent un défaut de fabrication:

• à la sortie de la machine A, 8% des ampoules présentent un défaut;
• à la sortie de la machine B, 5% des ampoules présentent un défaut.

On définit les événements suivants:

• $A$: « l'ampoule provient de la machine A»;
• $B$: « l'ampoule provient de la machine B»;
• $D$: « l'ampoule présente un défaut».

1. On prélève un ampoule au hasard parmi la production totale d'une journée.
   1. Construire un arbre pondéré représentant la situation.
   
   
   2. Montrer que la probabilité de tirer une ampoule sans défaut est égale à 0,9305.
   D’après la formule des probabilités totales on a :
   $\begin{align*} p\left(\overline{D}\right) &=p\left(A \cap \overline{D}\right)+p\left(B \cap \overline{D}\right) \\
   &=0,65\times 0,92+0,35\times 0,95 \\
   &=0,930~5
   \end{align*}$
   $\quad$
   
   3. L'ampoule tirée est sans défaut.
      Calculer la probabilité qu'elle provienne de la machine A.
   On veut calculer :
   $\begin{align*} p_{\overline{D}}(A) &=\dfrac{p\left(A \cap \overline{D}\right)}{p\left(\overline{D}\right)} \\
   &=\dfrac{0,65 \times 0,92}{0,930~5} \\
   &=\dfrac{0,598}{0,930~5} \\
   &\approx 0,642~7
   \end{align*}$
   $\quad$
2. On prélève 10 ampoules au hasard parmi la production d'une journée à la sortie de la machine A. La taille du stock permet de considérer les épreuves comme indépendantes et d'assimiler les tirages à tirages avec remise.
   Calculer la probabilité d'obtenir au moins 9 ampoules sans défaut.
On appelle $X$ la variable aléatoire comptant le nombre d’ampoules sans défaut.
On effectue $10$ tirages aléatoires, indépendants, identiques et possédant chacun exactement deux issues : $D$ et $\overline{D}$. On sait que $\left(\overline{D}\right)=0,930~5$.
$n=10$ et $p=0,930~5$.
Par conséquent $X$ suit la loi binomiale de paramètres $n=10$ et $p=0,930~5$.
On veut calculer :
$\begin{align*} P(X\geqslant 9) &=P(X=9)+P(X = 10)
&\approx 0,85
\end{align*}$
$\quad$

Partie B

1. On rappelle que si $T$ suit une loi exponentielle de paramètre $\lambda$ ($\lambda$ étant un réel strictement positif) alors pour tout réel positif $a$, $\displaystyle P(T\leqslant a)=\int\limits_0^a\lambda\text{e}^ {-\lambda x}\text{d}x$.
   1. Montrer que $P(T\geqslant a)=\text{e}^ {-\lambda a}$.
   $\begin{align*} P(T \geqslant a) &= 1-P(X\leqslant a) \\
   &=\displaystyle 1-\int_0^a \lambda\text{e}^{-\lambda x}\mathrm{d}x \\
   &=1-\big[-\text{e}^{-\lambda x}\big]_0^a \\
   &=1+\text{e}^{-\lambda a}-1 \\
   &=\text{e}^{-\lambda a}
   \end{align*}$
   $\quad$
   
   2. Montrer que si $T$ suit une loi exponentielle alors pour tous les réels positifs $t$ et $a$ on a \[ P_{T\geqslant t}(T\geqslant t+a)=P(T\geqslant a). \]
   Soit $t$ et $a$ deux réels positifs.
   $\begin{align*} \displaystyle P_{T \geqslant t}\left(T \geqslant t+a\right) &=\dfrac{P\left(\left(T \geqslant t\right)\cap \left(T \geqslant t+a\right)\right)}{P\left(T\geqslant t\right)} \\
   &=\dfrac{P\left(T\geqslant t+a\right)}{P\left(T \geqslant t\right)} \\
   &=\dfrac{\text{e}^{-\lambda(t+a)}}{\text{e}^{-\lambda t}} \\
   &=\text{e}^{-\lambda a} \\
   &=P\left(T\geqslant a\right)
   \end{align*}$
   $\quad$
2. Dans cette partie, la durée de vie en heures d'une ampoule sans défaut est une variable aléatoire $T$ qui suit la loi exponentielle d'espérance 10000 .
   1. Déterminer la valeur exacte du paramètre $\lambda$ de cette loi.
   On sait que $E(T)=10~000$. Or $E(T)=\dfrac{1}{\lambda}$ donc $\lambda =\dfrac{1}{10~000} = 10^{-4}$
   $\quad$
   
   2. Calculer la probabilité $P(T\geqslant 5000 )$.
   $P(T\geqslant 5~000)=\text{e}^{-5~000\times 10^{-4}}\approx 0,606~5$
   $\quad$
   
   3. Sachant qu'une ampoule sans défaut a déjà fonctionné pendant 7000 heures, calculer la probabilité que sa durée de vie totale dépasse 12000 heures.
   On veut calculer
   $\begin{align*} P_{T \geqslant 7~000}(T \geqslant 12~000) &= P_{T \geqslant 7~000}(T \geqslant 7~000+5~000) \\
   &= P(T \geqslant 5~000) \\
   &\approx 0,606~5
   \end{align*}$
   $\quad$

Partie C

L'entreprise a cherché à améliorer la qualité de sa production et affirme qu'il n'y a pas plus de 6% d'ampoules défectueuses dans sa production. Une association de consommateurs réalise un test sur un échantillon et obtient 71 ampoules défectueuses sur 1000 .

1. Dans le cas où il y aurait exactement 6% d'ampoules défectueuses, déterminer un intervalle de fluctuation asymptotique au seuil de 95% de la fréquence d'ampoules défectueuses sur un échantillon aléatoire de taille 1000 .
On a $n=1~000 \geqslant 30$ et $p=0,06$ donc $np=60 \geqslant 5$ et $n(1-p)=940 \geqslant 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :
$\begin{align*} I_{1~000} &=\left[0,06-1,96\times \sqrt{\dfrac{0,06\times 0,94}{1~000}};0,06+1,96\times \sqrt{\dfrac{0,06\times 0,94}{1~000}} \right] \\
&\approx [0,045~2;0,074~8]
\end{align*}$
$\quad$
2. A-t-on des raisons de remettre en cause l'affirmation de l'entreprise ?
La fréquence observée est $f=\dfrac{71}{1~000}=0,071\in I_{1~000}$
Au risque d’erreur de $5\%$ on ne peut pas remettre en cause l’affirmation de l’entreprise.
$\quad$